In a Euclidean plane which one of the following is not an equivalence relation? a Parallelism of lines a line being deemed parallel to itself b Congruence of triangles c Similarity of triangles d Orthogonality of lines
Correct option is dIn a Euclidean plane orthogonality of lines is not an equivalence relation
Related Solutions
In a Euclidean plane,which one of the following is not equivalence relation?
View SolutionShow that set of all parallel lines in any plane is an equivalence relation.
View SolutionRelation "parallel" in the straight line in a plane is :
View Solutionसमतल में स्थित सरल रेखाओं में सम्बन्ध ' समान्तर है ' होता है -
View SolutionRelation " parallel" in the straight line in a plane is :
View Solutionand are two parallel lines intersected by another pair of parallel lines and as shown in figure. Show that .
View SolutionI and m are two parallel lines intersected by another pair of parallel lines p and show that
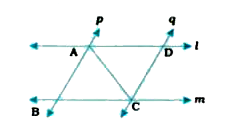 View Solution
View SolutionThe distance between the two parallel lines is 1 unit. A point A is chosen to lie between the lines at a distance 'd' from one of them Triangle ABC is equilateral with B on one line and C on the other parallel line. The length of the side of the equilateral triangle is
View SolutionThe distance between the two parallel lines is 1 unit. A point A is chosen to lie between the lines at a distance 'd' from one of them Triangle ABC is equilateral with B on one line and C on the other parallel line. The length of the side of the equilateral triangle is
View SolutionThe distance between the two parallel lines is 1 unit. A point 'A' is chosen to lie between the lines at a distance 'd' from one of them. Triangle ABC is equilateral with B on one line and C on the other parallel line. The length of the side of the equilateral triangle is
View SolutionThe distance between the two parallel lines is 1 unit A poin A is chosen to lie between the lines at a distance 'd' from one of them .Triangle ABC is equilateral with B on one line and C on the other parallel line .The length of the side of the equilateral triangle is
View SolutionThe distance between the two parallel lines is 1 unit. A point A is chosen to lie between the lines at a distance 'd' from one of them Triangle ABC is equilateral with B on one line and C on the other parallel line. The length of the side of the equilateral triangle is
View SolutionThe distance between the two parallel lines is 1 unit. A point A is chosen to lie between the lines at a distance 'd' from one of them Triangle ABC is equilateral with B on one line and C on the other parallel line. The length of the side of the equilateral triangle is
View SolutionThe distance between the two parallel lines is 1 unit. A point A is chosen to lie between the lines at a distance 'd' from one of them Triangle ABC is equilateral with B on one line and C on the other parallel line. The length of the side of the equilateral triangle is
View SolutionIntroduction|Congruence Of Plane Figures|Congruence Among Line Segment|Congruence Of Angle|Congruence Of Triangles|Question Practice|OMR
View SolutionLet be a relation on the set of all lines in a plane defined by <=> line is parallel to line . Show that is an equivalence relation.
View Solutionl,m అనే ఒక జత సమాంతర రేఖలు p మరియు q అనే వేరొక జత సమాంతర రేఖలచే ఖండించబడినవి. అయిన అని నిరూపించుము.
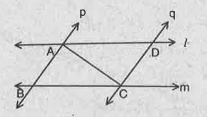 View Solution
View SolutionThe equation represents (A) a pair of straight lines (B) a pair of parallel lines (C) a pair of parallel planes (D) a pair of perpendicular planes
View SolutionThe eqution represents (A) a pair of straighat lines (B) a pair of parallel lines (C) a pair of parallel planes (D) a pair of perpendicular planes
View SolutionABC is an equilateral triangle such that the vertices B and C lie on two parallel lines at a distance 6. If A lies between the parallel lines at a distance 4 from one of them, then the length of a side of the equilateral triangle is :
View Solution
