l and m are two parallel lines intersected by another pair of parallel lines p and q as shown in figure. Show that △ABC≅△CDA.
To show that triangle ABC is congruent to triangle CDA, we will use the properties of parallel lines and the concept of alternate angles. Here’s the step-by-step solution:
Step 1: Identify the Angles
Since lines L and M are parallel and AC is a transversal, we can identify the angles formed by these lines.
Hint: Look for pairs of angles that are formed when a transversal intersects parallel lines.
Step 2: Use Alternate Angles
By the property of alternate angles, we have:
- Angle VAC = Angle DCA (Alternate angles)
Justification: Since L is parallel to M and AC is a transversal, the angles VAC and DCA are alternate interior angles.
Step 3: Identify Another Pair of Angles
Next, we can identify another pair of angles:
- Angle BCA = Angle DAC (Alternate angles)
Hint: Again, apply the property of alternate angles for the transversal AC with respect to the parallel lines L and M.
Step 4: Establishing the Third Angle
Now, we can use the fact that both triangles share a common side:
- Side AC is common to both triangles ABC and CDA.
Hint: Remember that if two triangles have two angles equal and the included side equal, they are congruent.
Step 5: Apply the Angle-Angle-Side (AAS) Congruence Criterion
Now we have:
1. Angle VAC = Angle DCA
2. Angle BCA = Angle DAC
3. Side AC is common.
Thus, by the Angle-Angle-Side (AAS) congruence criterion, we can conclude that:
- Triangle ABC ≅ Triangle CDA.
Hint: AAS states that if two angles and the included side of one triangle are equal to two angles and the included side of another triangle, the triangles are congruent.
Conclusion
Therefore, we have shown that triangle ABC is congruent to triangle CDA.
Since lines L and M are parallel and AC is a transversal, we can identify the angles formed by these lines.
By the property of alternate angles, we have:
- Angle VAC = Angle DCA (Alternate angles)
Next, we can identify another pair of angles:
- Angle BCA = Angle DAC (Alternate angles)
Now, we can use the fact that both triangles share a common side:
- Side AC is common to both triangles ABC and CDA.
Now we have:
1. Angle VAC = Angle DCA
2. Angle BCA = Angle DAC
3. Side AC is common.
- Triangle ABC ≅ Triangle CDA.
Therefore, we have shown that triangle ABC is congruent to triangle CDA.
Topper's Solved these Questions
Similar Questions
l and m are two parallel lines intersected by another pair of parallel lines p and q as shown in figure. Show that ABC≅CDA
View Solutionl, m and n are three parallel lines intersected by transversals p and q such that l, m and n cut off equal intercepts AB and BC on p (see Figure). Show that l, m and n cut off equal intercepts DE and EF on q also.
View SolutionPQ and RS are two parallel chords of a circle and lines RP and SQ intersect each other at O as shown in Figure. Prove that OP=OQ.
View SolutionABCD is a quadrilateral. A line through D, parallel to AC, meets BC produced in P as shown in figure. Prove that ar(△ABP)=a r (Quad.ABCD).
View SolutionTwo parallel lines l and m are intersected by a transversal p . Show that the quadrilateral formed by the bisectors of interior angles is a rectangle.
View SolutionPQ and RS are two parallel chords of a circle and lines RP and SQ intersect each other at O as shown in Figure. Prove that OP=OQ
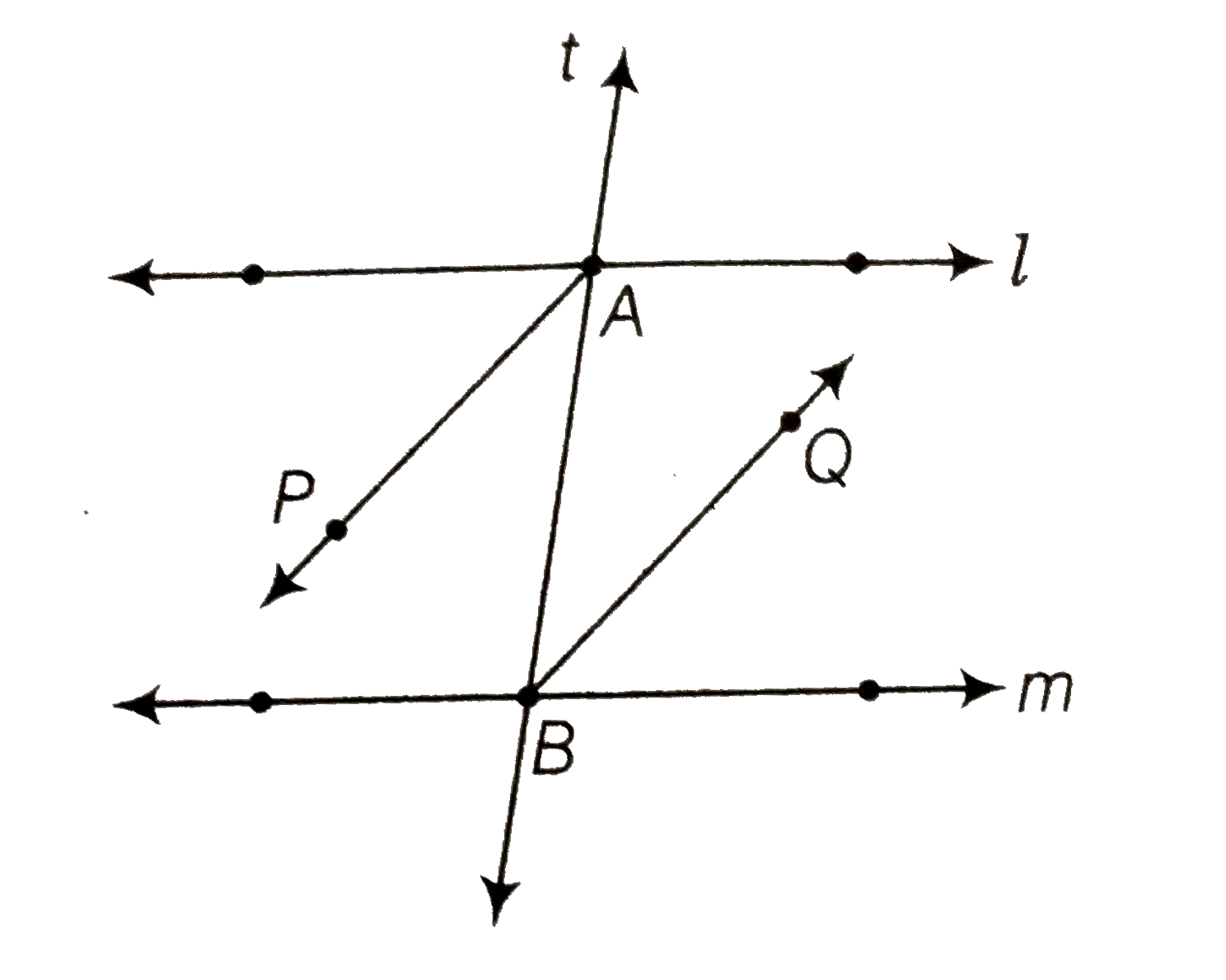
View SolutionAP and BQ are the bisectors of the two alternate interior angles formed by the intersection of a transversal t with parallel lines l and m (in the given figure). Show that AP||BQ.
View SolutionP is a point on the side BC of a triangle ABC such that AB=AP. Through A and C, lines are drawn parallel to BC and PA, respectively, so as to intersect at D as shown in Figure. Show that ABCD is a cyclic quadrilateral.
View SolutionP is a point on the side BC of a triangle ABC such that AB=AP. Through A and C, lines are drawn parallel to BC and PA, respectively, so as to intersect at D as shown in Figure. Show that ABCD is a cyclic quadrilateral.
View SolutionIn the given figure, AB and CD are parallel lines intersected by a transversal PQ at L and M respectively, If ∠CMQ=600 find all other angles in the figure.
View Solution