For the network shown determine using Thevenin’s theorem voltage across capacitor in. Fig. .ZCD = j5| | 10 + j5 = 1.25 + j3.75. This impedance is in series with the 10Ω resistance. Using voltage divider rule the drop over ZCD is
When load of −j5 Ω is removed the circuit becomes as shown in Fig.. Thevenin voltage is given by the voltage drop produced by 100-V source over 5 + j5impedance. It can be calculated as under.VCD = 1001.25 + j3.75/10 + 1.25 + j3.75 = 125 + j375/11.25 + j3.75This VCD is applied across j5 reactance as well as across the series combination of 5Ω and 5 + j5 Ω. Again using voltage-divider rule for VCD we getVAB = Vth =VCD x 5 + j5/10 x j5 = 125 + j375/11.25 + j3.75 x 5 + j5/10 + j5 = 21.1 ∠ 71.57º = 6.67 + j20As looked into terminals A and B the equivalent impedance is given by RAB = Rth = 5 + j5 | | 5 + 10 || j5 = 5 + j5 | | 7 + j4 = 3 + j 2.33The equivalent Thevenin’s source along with the load is shown in Fig.. Total impedance = 3 + j 2.33 − j 5 = 3 −j2.67 = 4.02 ∠− 41.67º ∴ I = 21.1∠71.57º/4.02∠−41.67º = 5.25∠113.24ºby Mesh Resistance Matrix The different items of the mesh resistance matrix [Rm] are as under : R11 = 10 + j 5; R22 = 10 + j 10 ; R33 = 5;R12 = R21 = −j 5; R23 = R32 = − 5 + j 5 ; R31 = R13 = 0. Hence the mesh equations in the matrix form are as given below :∴ Δ = 10 + j5 [510 + j10 − 5 + j5 5 + j5] + j5−j25 = 625 + j250 = 673∠21.8º= j 5 500 + j 500 = 3535 ∠ 135º ∴ I3 = Δ3/Δ = 3535∠135º/673∠21.8º = 5.25∠113.2º
Related Solutions
For the circuit shown in Fig. find
the voltage drop across series resistance,
 View Solution
View SolutionIn a series LCR circuit, the voltage across each of the resistance, capacitance and inductance is 10 V. If the capacitor is removed, the voltage across the inductor will be:
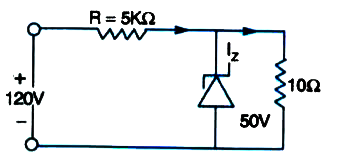
View SolutionFor the circuit shown in Fig. find 1) the output voltage, 2) the voltage drop across series resistance, 3) the current through Zener diode
View SolutionFor the circuit shown in Fig. find
1) the output voltage
2) the voltage drop across series resistance,
3) the current through Zener diode.
 View Solution
View SolutionIn series LCR circuit voltage drop across resistance is 8V, across inductor is 6V and across capacitor is 12V. Then
View SolutionIn series LCR circuit voltage drop across resistance is 8V, across inductor is 6V and across capacitor is 12V. Then
View SolutionA network of resistances is connected to a 16V battery with internal resistance of 1W as shown in Fig. Obtain the voltage drops VAB, VBC and VCD.
View SolutionObtain the equivalent capacitance of the network in Fig. For a 300 V supply, determine the charge and voltage across each 100 pF capacitor.
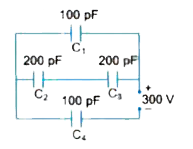 View Solution
View SolutionObtain the equivalent capacitance of the following network in Fig. For 300 V supply, determine the charge and voltage across each capacitor. :
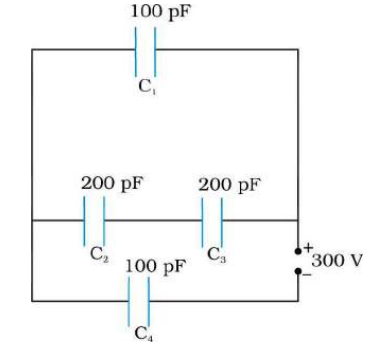 View Solution
View SolutionObtain equivalent capacitance of the following network, Fig. For a 300V supply determine the charge and voltage across each capacitor.
View SolutionObtain the equivalent capacitance of the network in Fig. 2.33. For a 300 V supply, determine the charge and voltage across each capacitor.
View SolutionObtain the equivalent capacitance of the network in Fig. For a 300 V supply. Determin the change and voltage across each capacitor.
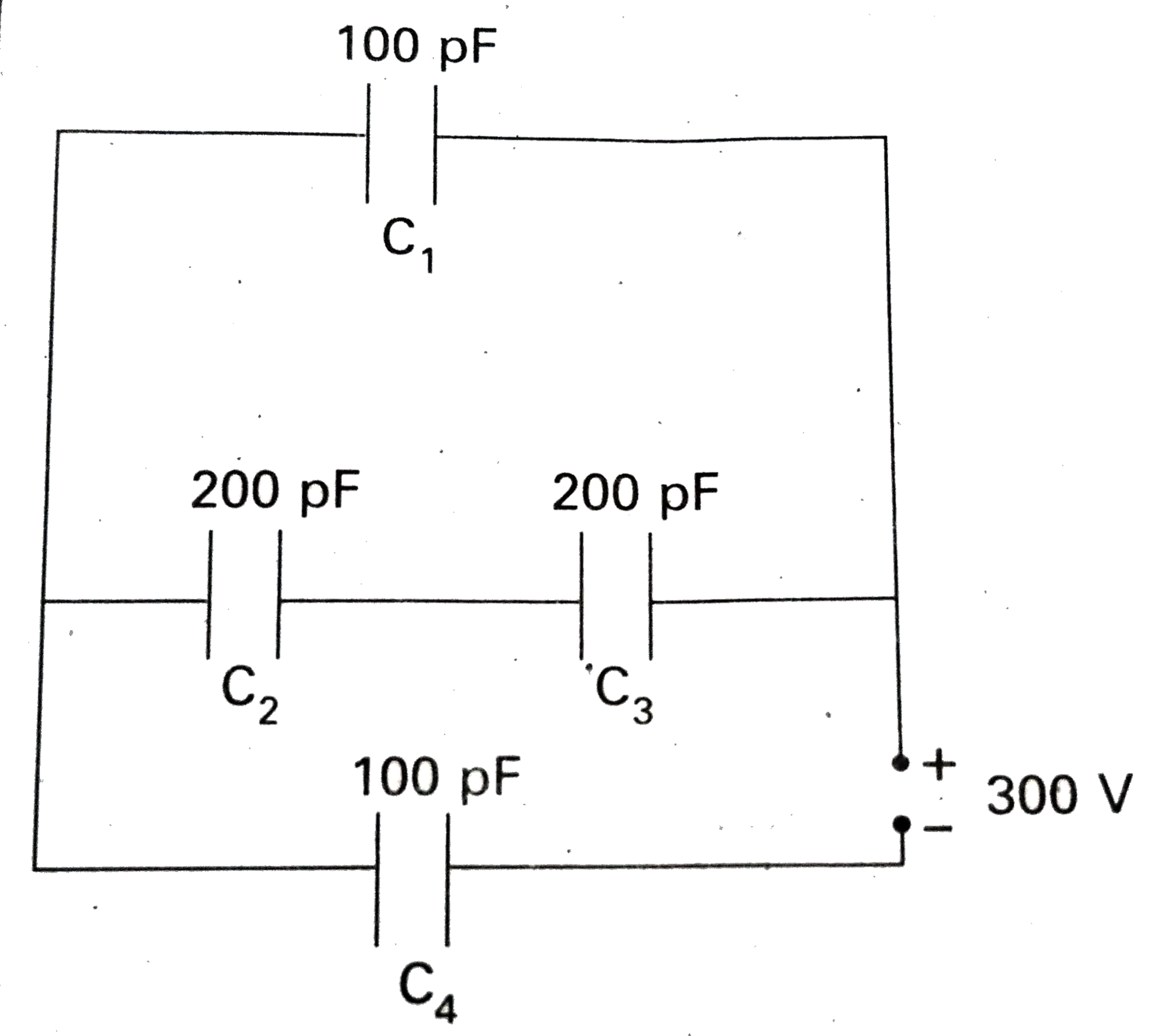 View Solution
View SolutionThe voltage drop across a forward biased diode is 0.7 volt. In the following circuit, the voltages across the 10 ohm resistance in series with the diode and 20 ohm resistance are :
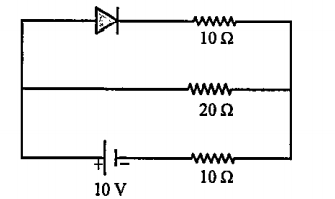 View Solution
View SolutionA diode is connected to 220V (rms) ac in series with a capacitor as shown in fig. The voltage across the capacitor is
View SolutionUsing kirchhoff's rules in the given circuit, determine . (a) the voltage drop across the unknow resistance R and . (b) the current l in the arm EF .
View SolutionUsing Kirchhoff's rules in the circuit shown determine (a) the voltage drop across the unknown resistor R, and (b) the current I in the arm EF.
View SolutionA a.c. power is connected non-inductive resistance and unknown capacitance in series. The voltage drop across the resistance is found to be , then voltage drop across capacitor is
View SolutionA 120V, 60 HzA.C. is connected across a non - inductive resistace of an un-known capacitor joined in series. The voltage across resistance is 66.3 V. The voltage drop across capacitor is
View SolutionIn the circuit shown in figure, the final voltage drop across the capacitor is :
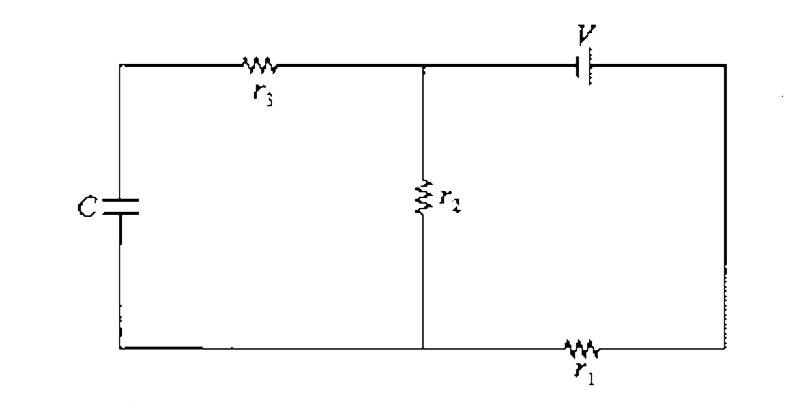 View Solution
View SolutionFind the voltage drop across a capacitor connected with a resistance and a battery of 60 V in series after a long time.
View Solution
