ABCD is a rhombus and P Q R and S are the mid-points of the sides AB BC CD and DA respectively. Show that the quadrilateral PQRS is a rectangle
Given : A rectangle ABCD in which P Q R S are the mid-points of AB BC CD and DA respectively PQ QR RS and SP are joined. To Prove : PQRS is a rhombus. Construction : Join ACProof : In ∆ABC P and Q are the mid-points of the sides AB and BC. ∴ PQ || AC and PQ = 1 2 AC …i [Mid point theorem] Similarly in ∆ADC SR || AC and SR = 1 2 AC …ii From i and ii we get PQ || SR and PQ = SR …iii Now in quadrilateral PQRS its one pair of opposite sides PQ and SR is parallel and equal [From iii] ∴PQRS is a parallelogram. Now AD = BC …iv [Opposite sides of a rectangle ABCD] ∴ 1/ 2 AD = 1/ 2 BC ⇒ AS = BQ In ∆APS and ∆BPQ AP = BP [∵ P is the mid-point of AB] AS = BQ [Proved above] ∠PAS = ∠PBQ [Each = 90°] ∆APS ≅ ∆BPQ [SAS axiom] ∴ PS = PQ …v From iii and v we have PQRS is a rhombus Proved.
Related Solutions
ABCD is a rectangle and P,R and S are the mid - points of the AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionABCD is a rhombus and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
View SolutionABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
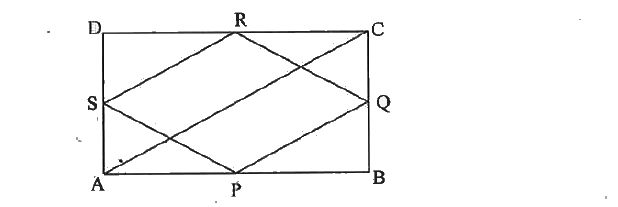
View SolutionABCD is a rectangle and P,Q,R and S are the mid points of the sides AB,BC,CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionABCD is a rhombus and P, Q, R and S are wthe mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
View SolutionABCD is a rectangle and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionABCD is a rhombus and P, Q, R, S are the mid-points of AB, BC, CD and DA respectively. Prove that quadrilateral PQRS is a rectangle.
View SolutionABCD is a rectangle and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionABCD is a rectangle and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionABCD is a rhombus and P,Q,R and S are the mid points of the sides AB,BC,CD and DA. Show that the quadrilateral PQRS is a rectangle.
View SolutionABCD एक समचतुर्भुज है। AB,BC,CD,DA के मध्य-बिंदु क्रमशः P,Q,R,S हैं। सिद्ध कीजिए कि PQRS एक आयत है।
View SolutionABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionABCD is a rhombus and P, Q, R, S are the mid-points of AB, BC, CD and DA respectively. Prove that quadrilateral PQRS is a rectangle.
View SolutionABCD is a rhombus and are the mid-points of respectively. Prove that is a rectangle.
View SolutionABCD एक आयत है जिसमें P,Q,R और S क्रमशः भुजाओं और DA के मध्य बिंदु है। दर्शाइए कि चतुर्भुज PQRS एक समचतुर्भुज है।
View SolutionABCD एक आयत है, जिसमें P, Q, R और S क्रमश : भुजाओ AB, BC, CD और DA के मध्य - बिंदु है । दर्शाइए कि चतुर्भुज PQRS एक समचतुर्भुज है ।
View SolutionP, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View SolutionP, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View SolutionLet ABCD be a rectangle. If the mid-points of the sides AB, BC, CD, DA are respectively P, Q, R, S, then what is the quadrilateral PQRS?
View Solution