ABCD is a quadrilateral in which P Q R and S are mid-points of the sides AB BC CD and DA respectively. see Fig.. AC is a diagonal. Show that : i SR || AC and SR = 1 2 AC ii PQ = SR iii PQRS is a parallelogram
Given : ABCD is a quadrilateral in which P Q R and S are mid-points of AB BC CD and DA. AC is a diagonal. To Prove : i SR || AC and SR = 1 2 AC ii PQ = SR iii PQRS is a parallelogram Proof : i In ∆ABC P is the mid-point of AB and Q is the mid-point of BC.∴ PQ || AC and PQ = 1/ 2 AC …1 [Mid-point theorem] In ∆ADC R is the mid-point of CD and S is the mid-point of AD ∴ SR || AC and SR = 1 2 AC …2 [Mid-point theorem] ii From 1 and 2 we get PQ || SR and PQ = SR iii Now in quadrilateral PQRS its one pair of opposite sides PQ and SR is equal and parallel. ∴ PQRS is a parallelogram. Proved.
Related Solutions
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA. AC is a diagonal. Show that
and
(ii) PQ=SR
PQRS is a parallelogram.

View SolutionABCD is a quadrilateral in which P,Q,R and S are mid points of the sides AB,BC,CD and DA. AC is a diagonal Show that:
PQ=SR
PQRS is a parallelogram
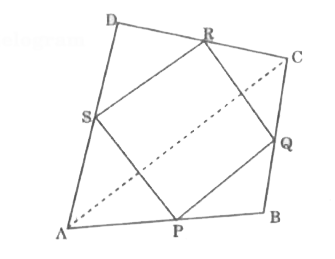
View SolutionABCD is a quadrilateral in which P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively (See Fig.
 AC is a diagonal Show that .
AC is a diagonal Show that .
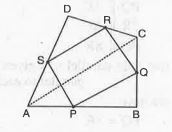
View SolutionABCD is a quadrilateral in which P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively (See Fig.
 AC is a diagonal Show that .
AC is a diagonal Show that .
View Solutionएक चतुर्भुज है जिसमें और क्रमश : भुजाओं और में मध्य - बिंदु है। उसका एक विकर्ण है। दर्शाइए कि
(i) और है
(ii) है |
(iii) PQRS एक समांतर चतुर्भुज है।
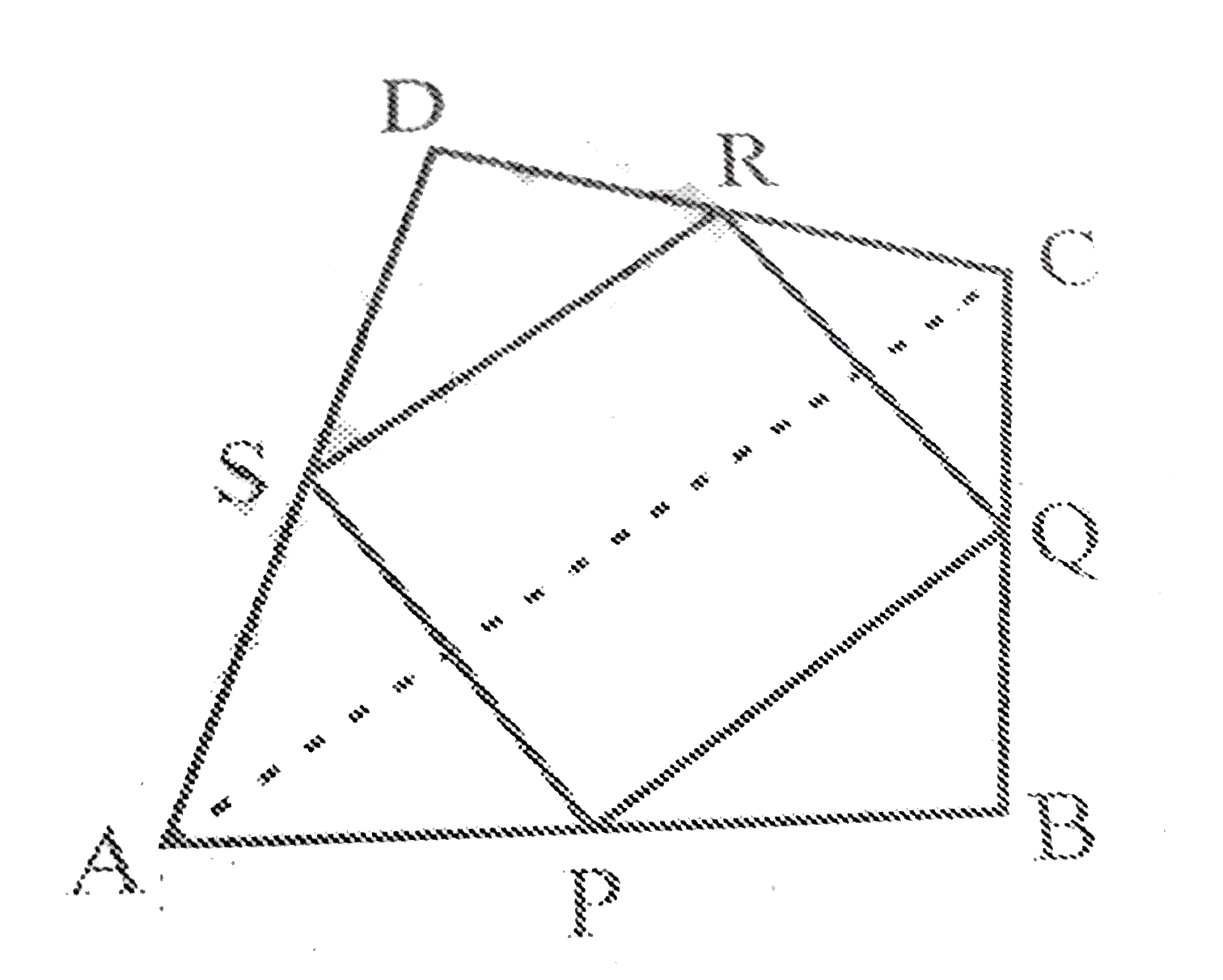
View SolutionABCD is a quadrilateral in which P,Q,R and S are the mid points of sides AB,BC,CD and DA respectively AC is a diagonal show that: PQ=SR
View SolutionABCD एक समांतर चतुभुर्ज है जिसकी भुजाओं तथा के मध्यबिन्दु क्रमश तथा है। सिद्ध कीजिए की
एवं एवं
(iii) एक समांतर चतुभुर्ज है।
View SolutionABCD is a quadrilateral in which P, Q, R and S are mid- points of the sides AB, BC, CD and DA. AC is a diagonal. Show that :
PQ=SR
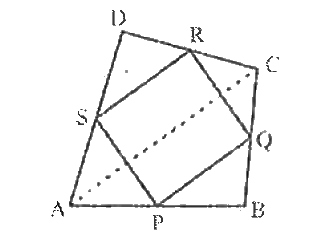
View SolutionABCD is a quadrilateral in which P,Q,R and S are the mid points of sides AB,BC,CD and DA respectively AC is a diagonal show that: SR||AC and SR=1/2AC
View SolutionABCD is a quadrilateral in which P,Q, R and S are midpoints of the sides AB , BC, CD and DA .AC is a diagonal. Śhow that
i) SR is parallel to AC, and SR= AC.
ii) P Q=SR
iii) PQRS is a parallelogram.
View SolutionABCD is a quadrilateral in which P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively (See Fig.)
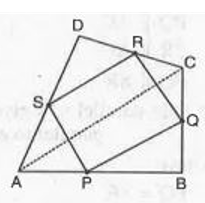 AC is a diagonal Show that PQ = SR.
AC is a diagonal Show that PQ = SR.
View SolutionABCD is a quadrilateral in which P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively (See Fig.)
 AC is a diagonal Show that PQ = SR.
AC is a diagonal Show that PQ = SR.
View SolutionABCD एक चतुर्भुज है। जिसमें P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य बिन्दु है। AC उसका एक विकर्ण है दर्शाइए कि:
(i) और
(ii) PQ = RS
(iii) PQRS एक समान्तर चतुर्भुज है।
View SolutionABCD ಒಂದು ಚತುರ್ಭುಜ.AB, BC, CD ಮತ್ತು DA. ಬಾಹುಗಳ ಮಧ್ಯಬಿಂದುಗಳು ಕ್ರಮವಾಗಿ P,Q, R ಮತ್ತು S ಆಗಿವೆ (ಚಿತ್ರ ಗಮನಿಸಿ). ಕರ್ಣ ಆದರೆ, SR AC ಮತ್ತು SR= AC.
 .
.
View SolutionABCD ਇੱਕ ਚਤੁਰਭੁਜ ਹੈ ਜਿਸ ਵਿਚ P,Q,R ਅਤੇ S ਕ੍ਰਮਵਾਰ ਭੁਜਾਵਾਂ AB, BC, CD ਅਤੇ DA ਦੇ ਮੱਧ ਬਿੰਦੂ ਹਨ(ਦੇਖੋ ਚਿੱਤਰ 8.29)। ਉਸਦਾ ਇਕ ਵਿਕਰਣ ਹੈ। ਦਰਸਾਉ ਕਿ SR || AC ਅਤੇ ਹੈ।

View SolutionABCD is a quadrilateral in which P,Q,R and S are the mid points of sides AB,BC,CD and DA respectively AC is a diagonal show that: PQRS is a parallelogram.
View SolutionABCD is a quadrilateral in which P, Q, R and S are mid- points of the sides AB, BC, CD and DA. AC is a diagonal. Show that :
PQRS is a parallelogram.
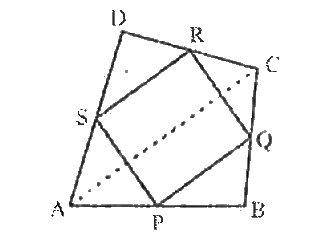
View SolutionABCD is a quadrilateral in which P, Q, R and S are mid- points of the sides AB, BC, CD and DA. AC is a diagonal. Show that :
and
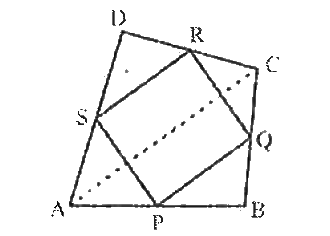
View SolutionIn quadrilateral ABCD if P,Q,R,S are mid-point of AB,BC,CD,DA resp. then SR is parallel to
View SolutionP, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View Solution