Question

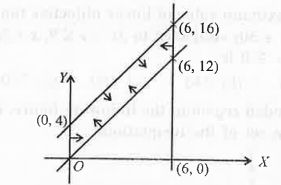
The feasible region for an LPP is shown in the Fig. 12.13. Let F = 3x – 4y be the objective function. Maximum value of F is.A 0 B 8 C 12 D – 18

Text Solution

Verified by Experts

Answer is C

Related Solutions

The feasible region for an $L P P$ is shown in the following figure. Let $F = 3 x - 4 y$ be the objective function. Maximum value of $F$ is

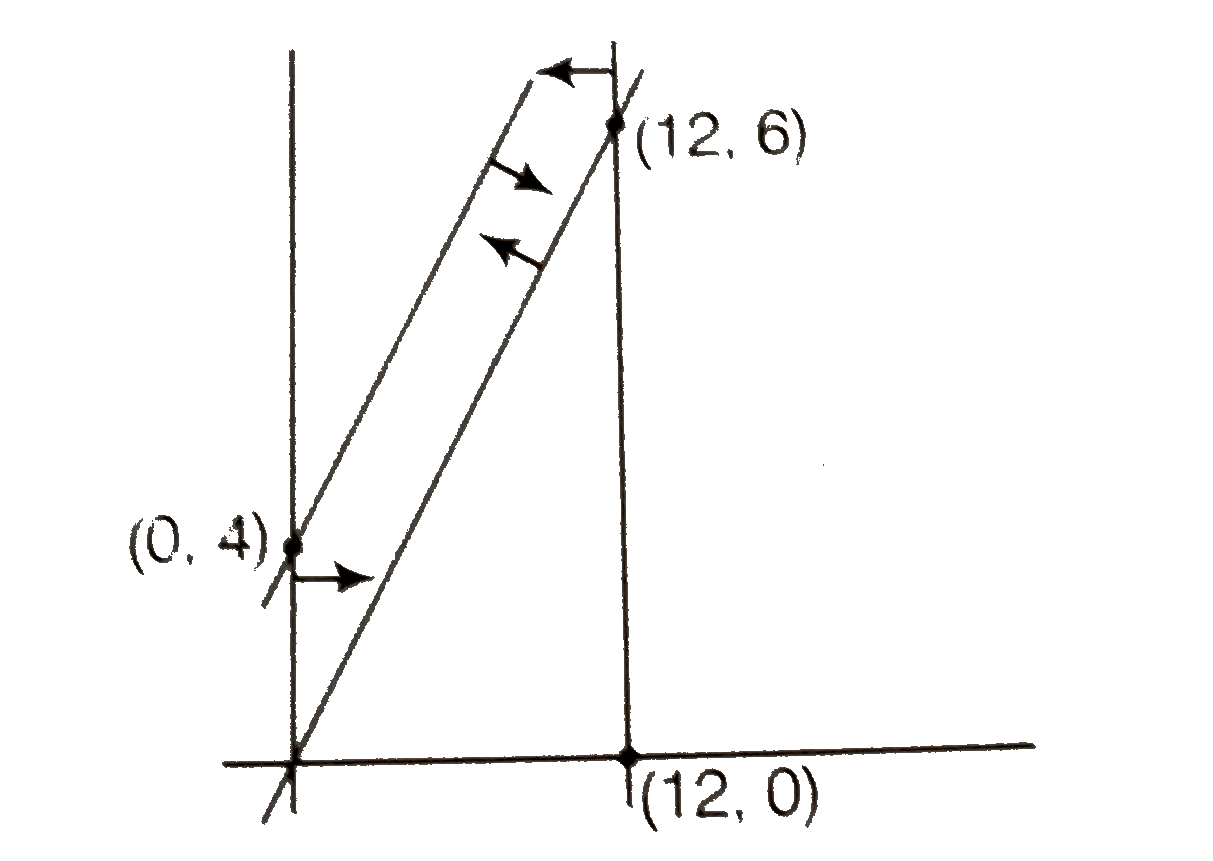
View Solution
The feasible region for an LPP is shown in the following figure. Let $F = 3 x - - 4 y$ be the objective function. Maximum value of F is

View Solution
The feasible region for an LPP is shown in the below. Let F = 3x - 4y be the objective function. Maximum value of F is :

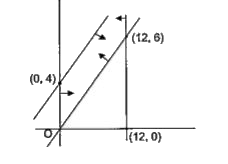
View Solution
The feasible region for an LPP is shown shaded in the figure 12.83. Let f=3x-4y be the objective function, the maximum vlaue of f is
View Solution
The feasible region for an LPP is shown in the figure. Let F = 3 x - 4 y be the objective function. Maximum value of F is:

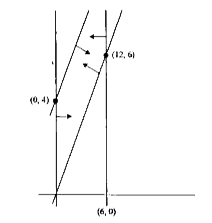
View Solution
The feasible solution for a LPP is shown in Fig. Let. Z = 3x-4 y be the objective function. Minimum value of F is

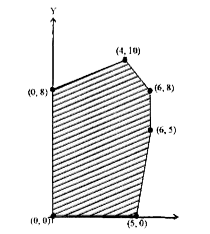
View Solution
The feasible region for an LPP is shown in the figure . Let F = 3 x - 4 y be the objective function. Minimum value of F is:

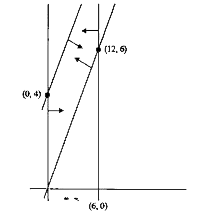
View Solution
The feasible region for an LPP is shown in the following figure. Let F=3 x-4 y be the objective function. Maximum value of F is

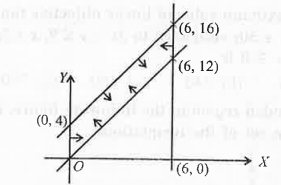
View Solution
The feasible solution for a LPP is shown in the following figure. Let $Z = 3 x - 4 y$ be the objective function.
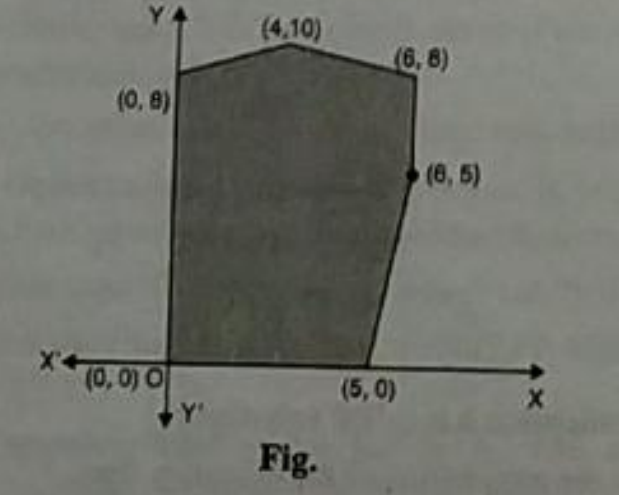Maximum of Z occurs at:
View Solution
The feasible solution for a LPP is shown in Figure
Let z = -3x - 4y

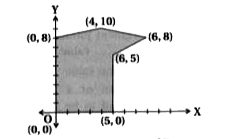
objective function. Maximum of Z occurs at
View Solution
The feasible solution for a LPP is shown in Fig. Let. Z = 3x-4 y be the objective function. Maximum of Z occurs at:

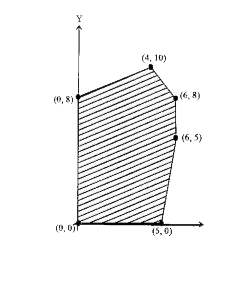
View Solution
The feasible region for an LLP is shown in the Figure. Let z = 3x - 4y be the objective function. Maximum value of z is

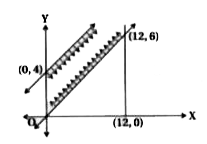
View Solution
Let A(0, 75), B(90, 0) , C(60, 40) and D(45, 25) be the corner points of the bounded feasible region of a LPP . If the objective function is $Z = 3 x + 4 y$ , then Z is maximum at corner point-
View Solution
The feasible solution for a LPP is shown in Fig. Let $Z = 4 x + y$ be the objective function. Maximum value of Z is 130.

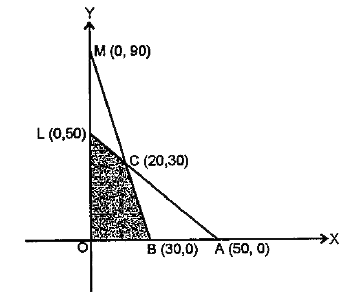
View Solution
Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5).
Let F = 4x + 6y be the objective function. (Maximum of F)-(Minimum of F) =
View Solution
The feasible solution for a LPP is shown in Fig. Let, Z=3x-4 y be the objective function. (Maximum value of Z+ Minimum value of Z) is equal to :

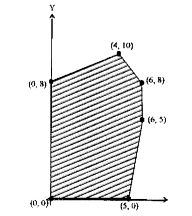
View Solution
The feasible region for an LPP is shown in the following figure. Let F=3 x-4 y be the objective function. Minimum value of F is

View Solution
Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6, 8) and (0, 5).
Let F = 4x + 6y be the objective function.
The Maximum of F - Minimum of F = 60
View Solution
Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6,0), (6, 8) and (0,5).
Let $F = 4 x + 6$ y be the objective function.
The Maximum of F - Minimum of F =
View Solution

The feasible region for an LPP is shown in the Fig. 12.13. Let F = 3x – 4y be the objective function. Maximum value of F is.A 0 B 8 C 12 D – 18

Answer is C

Related Solutions

Recommended Content