In a certain binary star system each star has the same mass as the distance between earth and the sun. What is their period of revolution in years ?
From Eqs. i and ii
Related Solutions
In a certain binary-star system, each star has the same mass as our Sun, and they revolve about their center of mass. The distance between them is the same as the distance between Earth and the Sun. What is their period of revolution in years ?
View SolutionIn a certain binary star system, each star has the same mass as our sun. They revolve about their centre of mass. The distance between them is the same as the distance between earth and the sun. What is their period of revolution in years ?
View SolutionIn a certain binary star system, each star has the same mass as our sun. They revolve about their centre of mass. The distance between them is the same as the distance between earth and the sun. What is their period of revolution in years ?
View SolutionIn a binary star system one of the stars has mass equal to mass of sun (M) . Separation between the stars is four times the average separation between earth and sun. Mass of the other star so that time period of revolution of the stars each other is equal to one earth year is
View SolutionIn a binary star system one of the stars has mass equal to mass of sun (M) . Separation between the stars is four times the average separation between earth and sun. Mass of the other star so that time period of revolution of the stars each other is equal to one earth year is
View SolutionA binary star has a time period years (time period of earth is one year) while distance between the two stars is 9 times distance between earth and the sun. Mass of one star is equal to mass of the sun and mass of other is times mass of the sun then calculate .
View SolutionTwo stars of a binary system are separated by a distance of 20 AU with a period of revolution of 20 years. One of the two stars is 4 times farthest from the centre of mass of the other. Find masses of each star.
View SolutionA binary star has a time period yeas (time period of earth is one year) while distance between the earth and the sun. Mass of one star is equal to mass of the sun and mass of other is times mass of the sun then calculate .
View SolutionConsider a binary star system consisting of two stars of masses and separated by a distance of with a period of revolution equal to 30 years. If one of the two stars is 5 times farther from the centre of mass than the other, show that the masses of the two stars are 5 and 25 times that of the sun.
View SolutionA trinary star system which is a system of three orbiting around centre of mass of system has time peroid of 3 years, while the distance between any two stars of the system is 2 astronomical unit. All the three stars are identical and mass of the sun is M and total mass of this multiple star system is (a)/(b)xxM . Then find (b)/(3) ? (a and b are lowest possible integers (I astronomical unit is equal to distance between sun and earth, time period of rotation of earth around sun is 1year)
View SolutionA trinary star system which is a system of three orbiting around centre of mass of system has time peroid of 3 years, while the distance between any two stars of the system is 2 astronomical unit. All the three stars are identical and mass of the sun is M and total mass of this multiple star system is (a)/(b)xxM . Then find (b)/(3) ? (a and b are lowest possible integers (I astronomical unit is equal to distance between sun and earth, time period of rotation of earth around sun is 1year)
View SolutionA trinary star system which is a system of three orbiting around centre of mass of system has time peroid of 3 years, while the distance between any two stars of the system is 2 astronomical unit. All the three stars are identical and mass of the sun is M and total mass of this multiple star system is (a)/(b)xxM . Then find (b)/(3) ? (a and b are lowest possible integers (I astronomical unit is equal to distance between sun and earth, time period of rotation of earth around sun is 1year)
View SolutionThe small dense stars rotate about their common centre of mass as a binary system, each with a period of year. One star has mass double than that of the other, while mass of the lighter star is one-third the mass of the Sun. The distance between the two stars is and the distance of the earth from the Sun is , find the relation between and .
View SolutionThe small dense stars rotate about their common centre of mass as a binary system, each with a period of year. One star has mass double than that of the other, while mass of the lighter star is one-third the mass of the Sun. The distance between the two stars is and the distance of the earth from the Sun is , find the relation between and .
View SolutionThe small dense stars rotate about their common centre of mass as a binary system, each with a period of 1 year. One star has mass double than that of the other, while mass of the lighter star is one-third the mass of the Sun. The distance between the two stars is r and the distance of the earth from the Sun is R , find the relation between r and R .
View SolutionLet a star be much brighter than our sun but its mass is same as that of sun If our earth has average lift span of man as In the earth like planet of this star system having double the distance from our star find the average lift span of a man on this planet in terms of our year
 .
.
View SolutionLet a star be much brighter than our sun but its mass is same as that of sun If our earth has average lift span of man as 70 years In the earth like planet of this star system having double the distance from our star find the average lift span of a man on this planet in terms of our year .
View SolutionIn a binary star system one star has thrice the mass of other. The stars rotate about their common centre of mass then :
View SolutionIn a binary star system one star has thrice the mass of other. The stars rotate about their common centre of mass then :
View SolutionA certain triple-star system consists of two stars, each of mass m, revolving about a central star, mass M, in the same circular orbit. The two stars stay at opposite ends of a diameter of the circular orbit, see figure. Derive an expression for the period of revolution of the stars, the radius of the orbit is r.
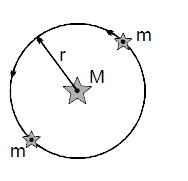
View Solution