In a binary star system one star has thrice the mass of other. The stars rotate about their common centre of mass then :
Both stars have same angular momentum about common centre of mass
Both stars have angular momentum of same magnitude about common centre of mass
Both stars have same angular speeds
Both stars have same linear speeds
The correct Answer is:C
To solve the problem regarding the binary star system where one star has thrice the mass of the other, we need to analyze the situation step by step:
Step 1: Understanding the Masses
Let the mass of the smaller star be m and the mass of the larger star be 3m.
Step 2: Center of Mass Calculation
The center of mass (CM) of a two-body system can be found using the formula:
rCM=m1r1+m2r2m1+m2
where r1 and r2 are the distances of the masses from the center of mass.
Since the total mass is m+3m=4m, we can set the distances from the center of mass as r1 for mass m and r2 for mass 3m. The center of mass will be closer to the more massive star.
Using the ratio of distances:
r1r2=m2m1=3mm=3
Let r1=x and r2=3x. The total distance r between the two stars is:
r=r1+r2=x+3x=4x
Thus, we can express r1 and r2 in terms of r:
r1=r4,r2=3r4
Step 3: Angular Speed and Linear Speed
In a binary star system, both stars rotate about their common center of mass with the same angular speed ω.
The linear speed v of each star is given by:
v=ωr
For the smaller star:
v1=ωr1=ωr4
For the larger star:
v2=ωr2=ω3r4
Since v1≠v2, the linear speeds are not the same.
Step 4: Angular Momentum Calculation
The angular momentum L of each star about the center of mass is given by:
L=Iω
where I is the moment of inertia.
The moment of inertia I for each star is:
I1=mr21=m(r4)2=mr216
I2=3mr22=3m(3r4)2=3m⋅9r216=27mr216
Now, calculating the angular momentum for both stars:
L1=I1ω=mr216ω
L2=I2ω=27mr216ω
Since L1≠L2, the angular momenta are not the same.
Conclusion
From the analysis:
1. Both stars do not have the same linear speed.
2. Both stars do not have the same angular momentum.
3. Both stars have the same angular speed.
Thus, the only correct option is that both stars have the same angular speed.
Let the mass of the smaller star be m and the mass of the larger star be 3m.
The center of mass (CM) of a two-body system can be found using the formula:
rCM=m1r1+m2r2m1+m2
where r1 and r2 are the distances of the masses from the center of mass.
r1r2=m2m1=3mm=3
Let r1=x and r2=3x. The total distance r between the two stars is:
r=r1+r2=x+3x=4x
Thus, we can express r1 and r2 in terms of r:
r1=r4,r2=3r4
In a binary star system, both stars rotate about their common center of mass with the same angular speed ω.
v=ωr
For the smaller star:
v1=ωr1=ωr4
For the larger star:
v2=ωr2=ω3r4
Since v1≠v2, the linear speeds are not the same.
The angular momentum L of each star about the center of mass is given by:
L=Iω
where I is the moment of inertia.
I1=mr21=m(r4)2=mr216
I2=3mr22=3m(3r4)2=3m⋅9r216=27mr216
L1=I1ω=mr216ω
L2=I2ω=27mr216ω
From the analysis:
1. Both stars do not have the same linear speed.
2. Both stars do not have the same angular momentum.
3. Both stars have the same angular speed.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.36
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.37
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.34
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
In a certain binary star system, each star has the same mass as our sun. They revolve about their centre of mass. The distance between them is the same as the distance between earth and the sun. What is their period of revolution in years ?
View SolutionIn a double star system one of mass m1 and another of mass m2 with a separation d rotate about their common centre of mass. Then rate of sweeps of area of star of mass m1 to star of mass m2 about their common centre of mass is
View SolutionIn a particular double star system two stars of mass 3.22×1030 kg each revolve about their common centre of mass 1.12×1011 on away.
(i). Calculate their common period of revolution, in years
(ii). Suppose that a meteoroid (small solid particle in space) passes through this centre of mass moving at right angles to the orbital plane of the stars. What must its speed be if it is to escape from the gravitational field of the double star?
View SolutionA pair of stars rotates about a common centre of mass. One of the stars has a mass M and the other has mass m such that =2m. The distance between the centres of the stars is d ( d being large compare to the size of eithe star).
The period of rotation of the stars about their common centre of mass ( in terms of d,m,G) is
View SolutionIn a double star, two stars one of mass m1 and another of mass m2, with a separation d, rotate about their common centre of mass. Find
(a) an expression for their time period of revolution.
(b) the ratio of their kinetic energies.
(c) the ratio of their angular momenta about the centre of mass.
(d) the total angular momentum of the system.
(e) the kinetic energy of the system.
View Solution_E01_055_Q01.png)
For the double star system, the two stars having masses m1 and m2are separated b a distance r. They are revolving about their common centre of mass in radii r1 and r2 respectively. Which of the following is/are incorrect.?
View SolutionA common Star Fish is
View SolutionA pair of stars rotates about their centre of mass One of the stars has a mass M and the other has mass m such that M=2m The distance between the centres of the stars is d (d being large compared to the size of either star) .
The ratio of the angular momentum of the two stars about their common centre of mass (Lm/Lm) is .
View SolutionCalculate centre of mass of the system
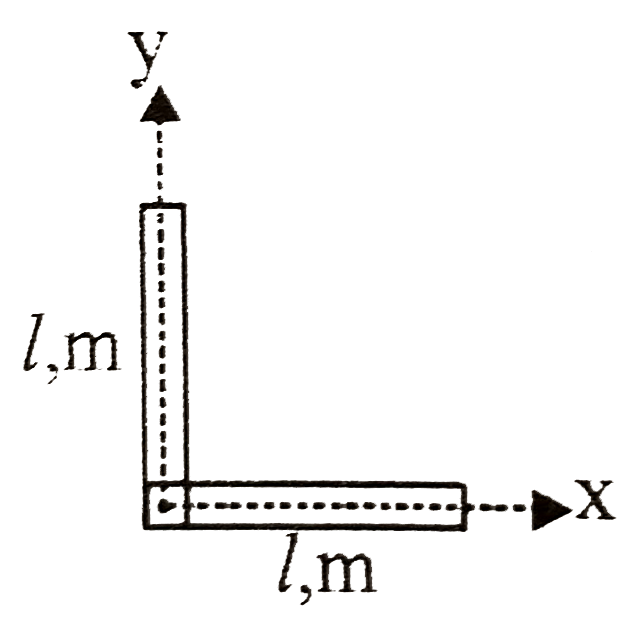
View SolutionIn a binary star system one of the stars has mass equal to mass of sun (M). Separation between the stars is four times the average separation between earth and sun. Mass of the other star so that time period of revolution of the stars each other is equal to one earth year is
View Solution
