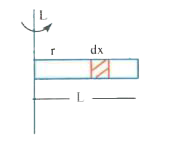
A thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
Let us consider an element of the rod at a distance r from it’s rotation axis. As the element rotates in a horizontal circle of radius r we have from Newton’s second law in projection form directed toward the axis of rotation :At the free end tension becomes zero. Integrating the above experession we get thuswhere S is the cross sectional area of the rod and T is the tension in the rod at the considered element
Related Solutions
A thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity omega in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity omega in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionA thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity omega in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity omega about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity omega about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA uniform rod of mass and length rotates in a horizontal plane with an angular velocity about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA thin uniform rod of length L and radius r rotates with an angular velocity in a horizontal plane about a vertical axis passing through one of its ends. The density of the material is and Youngs modulus is Y. 1) Find tension in the rod at distance Y from the axis. 2) Find elongation of the rod
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:
View SolutionA conical pendulum, a thin uniform rod of length l and mass m , rotates uniformly about a vertical axis with angular velocity omega (the upper end of the rod is hinged). Find the angle theta between the rod and the vertical.
View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionA uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
View Solutionद्रव्यमान M व लम्बाई L की पतली छड़ की घूर्णन त्रिज्या छड़ की लम्बाई के लम्बवत् तथा छड़ के एक सिरे से गुजरने वाले अक्ष के परितः ज्ञात कीजिये।
View SolutionA uniform rod of mass m. length L, area of cross- secticn A is rotated about an axis passing through one of its ends and perpendicular to its length with constant angular velocity in a horizontal plane If Y is the Young's modulus of the material of rod, the increase in its length due to rotation of rod is
View SolutionA uniform rod of mass m. length L, area of cross- secticn A is rotated about an axis passing through one of its ends and perpendicular to its length with constant angular velocity o in a horizontal plane If Y is the Young's modulus of the material of rod, the increase in its length due to rotation of rod is
View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed in the horizontal plane then the angular momentum of the rod about the axis is:
View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed in the horizontal plane then the angular momentum of the rod about the axis is:
View SolutionA uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle theta with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:
View SolutionA rod of length l and mass is rotated in a horizontal plane about its one end with constant angular velocity . The tension at the middle section of the rod is
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod is released from rest in the Position shown by slightly displacing it clockwise. Find the hinge reaction at the axis of rotation at the instant the rod turns through. 90^@
View SolutionA uniform rod of length , mass , cross-sectional area and Young's modulus is rotated in horizontal plane about a fixed vertical axis passing through one end, with a constant angular velocity . Find the total extension in the rod due to the tension produced in the rod.
View Solution