A homogeneous rod of length 2l leans against a vertical wall at one end and against a smooth stationary surface at another end.What function y x must be used to describe the cross section of this surface for the rod to remain in equilibrium in any position even in the absence of friction? Assume that the rod remains all the time in the same vertical plane perpendicular to the plane of the wall.
Let the cross section of the surface be described by the function y x shown in Fig. 184. Since the rod must be in equilibrium in any position the equilibrium can be only neutral i.e. the centre of mass of the rod must be on the same level for any position of the rod. If the end of the rod leaning against the surface has an abscissa x the ordinate y0 of its other end touching the vertical wall can be found from the conditionSince the rod is homogeneous its centre of mass is at the midpoint. Assuming for definiteness that the ordinate of the centre of mass is zero we obtainOnly the solution with the minus sign has the physical meaning. Therefore in general the cross section of the surface is described by the functionwhere a is an arbitrary constant.
Related Solutions
A homogeneous rod of length 2l leans against a vertical wall at one end and against a smooth stationary surface at another end. What function y (.x) must be used to describe the cross section of this surface for the rod to remain in equilibrium in any position even in the absence of friction? Assume that the rod remains all the time in the same vertical plane perpendicular to the plane of the wall.
View SolutionA rod of length I leans by its upper end against a smooth vertical wall, while its other end leans against the floor. The end that leans against the wall moves uniformly downward. Then:
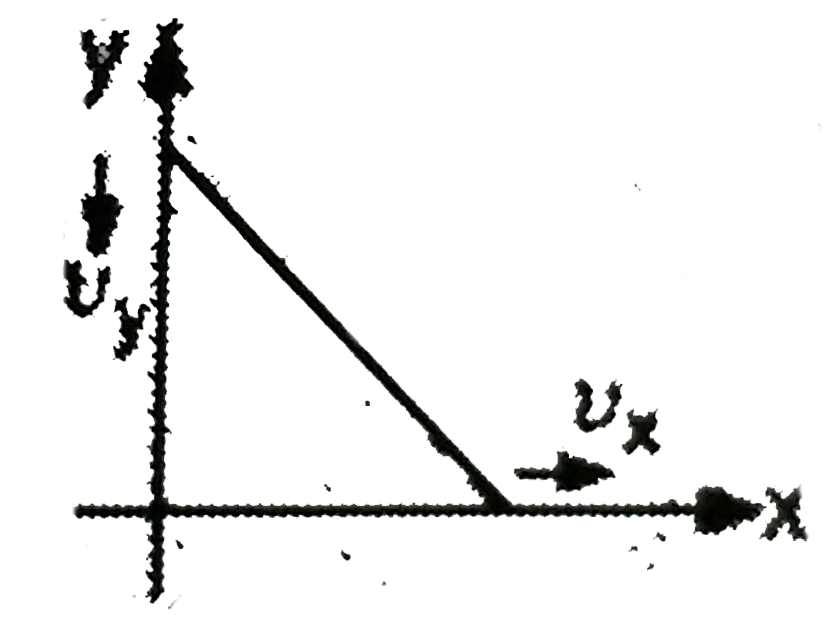
View SolutionA rod of length I leans by its upper end against a smooth vertical wall, while its other end leans against the floor. The end that leans against the wall moves uniformly downward. Then:
View SolutionA stationary uniform rod of mass 'm', length 'l' leans against a smooth vertical wall making an angle with horizontal floor. Find the normal force & frictional force that is exerted by the floor on the rod ?
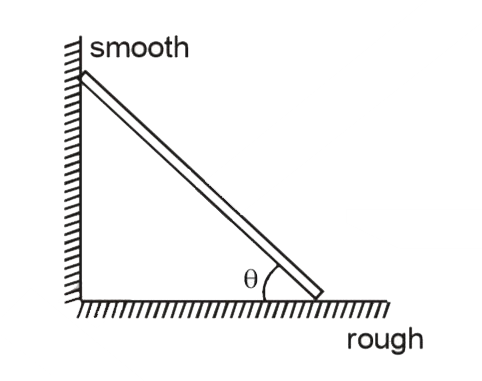
View SolutionA rod of length l is released from the vertical position on a smooth horizontal plane. What is the nature of motion of the free end of the rod ?
View SolutionThe velocity of end 'A' of rigid rod placed between two smooth vertical walls moves with velocity 'u' along vertical direction. Find out the velocity of end 'B' of that rod, rod always remains in constant with the vertical walls.
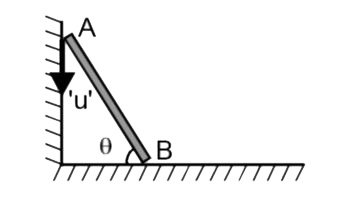
View Solutionएक समरूप छड़ का द्रव्यमान M, अनुप्रस्थ काट का क्षेत्रफल A तथा लंबाई L है। इसे एक सिरे से क्लैंप कर ऊर्ध्वाधर स्थिति में लटकाया गया है। यदि इस छड़ के पदार्थ का यंग गुणांक Y हो, तो अपने भार के कारण छड़ की लंबाई में वृद्धि निकालें।
View SolutionA uniform rod AB of length a hangs with one end against a smooth vertical wall, being supported by a string of length l, attached to the other end of the rod and to a point of the rod vertically above B. If the rod rests inclined to the wall at angle then
View SolutionA horizontal rod of mass 10g and length 10cm is placed on a smooth plane inclined at an angle of 60^@ with the horizontal with the length of the rod parallel to the edge of the inclined plane. A uniform magnetic field induction B is applied vertically downwards. If the current through the rod is 1*73ampere , the value of B for which the rod remains stationary on the inclined plane is
View SolutionA horizontal rod of mass and length is placed on a smooth plane inclined at an angle of with the horizontal with the length of the rod parallel to the edge of the inclined plane. A uniform magnetic field induction B is applied vertically downwards. If the current through the rod is , the value of B for which the rod remains stationary on the inclined plane is
View SolutionA horizontal rod of mass and length is placed on a smooth plane inclined at an angle of with the horizontal with the length of the rod parallel to the edge of the inclined plane. A uniform magnetic field induction B is applied vertically downwards. If the current through the rod is , the value of B for which the rod remains stationary on the inclined plane is
View SolutionA horizontal rod of mass and length is placed on a smooth plane inclined at an angle of with the horizontal with the length of the rod parallel to the edge of the inclined plane. A uniform magnetic field induction B is applied vertically downwards. If the current through the rod is , the value of B for which the rod remains stationary on the inclined plane is
View SolutionIn the arrangement shown in figure, the rod of mass held by two smooth walls, remains always perpendicular to the surface of the wedge of mass . Assuming all the surface to be frictionless, find the acceleration of the rod and that of the wedge.

View SolutionIn the arrangement shown in the figure , the rod of mass held by two smooth walls , remain always perpendicular to the surface of the wedge of mass . Assuming all the surface are frictionless, find the acceleration of the rod wedge.

View SolutionIn the arrangement shown in figure, the rod of mass m held by two smooth walls, remains always perpendicular to the surface of the wedge of mass M . Assumming all the surface to be frictionless, find the acceleration of the rod and that of the wedge.
View Solutionwith horizontal 30^(@) The smooth plane is inclined at an angle. A thin current carrying metallic rod is kept parallel to the horizontal surface. The plane is located in a uniform magnetic field of 0.15 T in the vertical direction. For what value of current will the rod remain stationary? The mass per unit length of the rod is 0.30 kg/m.
View SolutionA rigid rod leans against a vertical wall (y-axis) as shwon in figure. The other end of the rod is ion the horizontal floor. Point A is pushed downwards with constant velocity. Path of the centre of the rod is

View SolutionA rigid rod leans against a vertical wall (y-axis) as shwon in figure. The other end of the rod is ion the horizontal floor. Point A is pushed downwards with constant velocity. Path of the centre of the rod is
View SolutionA uniform solid rod of mass 40kg and length 10m rests against a vertical smooth wall making an angle of with the vertical. Find the force of friction (f) and normal reaction (R ) exerted by the groundd on the rod.
View SolutionA rod is hinged vertically at one end and is forced to oscillate in a vertical plane with hinged end at the top, the motion of the rod:
View Solution