A horizontal rod of mass 10g and length 10cm is placed on a smooth plane inclined at an angle of 60∘ with the horizontal with the length of the rod parallel to the edge of the inclined plane. A uniform magnetic field induction B is applied vertically downwards. If the current through the rod is 1⋅73ampere, the value of B for which the rod remains stationary on the inclined plane is
1.73 T
11.73T
1.T
None of the above
The correct Answer is:C
To solve the problem, we need to find the value of the magnetic field induction B that keeps the rod stationary on the inclined plane. We will use the balance of forces acting on the rod.
1. Identify the Forces Acting on the Rod:
- The weight of the rod W=mg acts vertically downwards.
- The magnetic force FB acts perpendicular to the direction of the current and the magnetic field.
2. Resolve the Weight of the Rod:
- The weight of the rod can be resolved into two components:
- Perpendicular to the inclined plane: W⊥=mgcos(60∘)
- Parallel to the inclined plane: W∥=mgsin(60∘)
3. Magnetic Force on the Rod:
- The magnetic force acting on the rod is given by:
FB=I⋅L⋅B⋅sin(90∘)=I⋅L⋅B
- Since the rod is horizontal and the magnetic field is vertical, the angle between the current direction and the magnetic field is 90∘.
4. Set Up the Equation for Equilibrium:
- For the rod to remain stationary, the magnetic force must balance the component of the weight acting down the incline:
FB=W∥
- Therefore, we have:
I⋅L⋅B=mgsin(60∘)
5. Substitute Known Values:
- Given:
- Mass m=10g=10×10−3kg
- Length L=10cm=10×10−2m
- Current I=1.73A
- g≈10m/s2
- sin(60∘)=√32
- Plugging in the values:
1.73⋅(10×10−2)⋅B=(10×10−3)⋅10⋅√32
6. Simplify the Equation:
- This simplifies to:
1.73⋅10−1⋅B=5√3×10−3
- Rearranging gives:
B=5√3×10−31.73×10−1
7. Calculate the Value of B:
- Calculating the right-hand side:
B=5√31.73×10−2
- Approximating √3≈1.732:
B≈5×1.7321.73×10−2≈5×10−2≈0.05T
8. Final Result:
- Thus, the value of B for which the rod remains stationary on the inclined plane is approximately 1T.
- The weight of the rod W=mg acts vertically downwards.
- The magnetic force FB acts perpendicular to the direction of the current and the magnetic field.
- The weight of the rod can be resolved into two components:
- Perpendicular to the inclined plane: W⊥=mgcos(60∘)
- Parallel to the inclined plane: W∥=mgsin(60∘)
- The magnetic force acting on the rod is given by:
FB=I⋅L⋅B⋅sin(90∘)=I⋅L⋅B
- Since the rod is horizontal and the magnetic field is vertical, the angle between the current direction and the magnetic field is 90∘.
- For the rod to remain stationary, the magnetic force must balance the component of the weight acting down the incline:
FB=W∥
- Therefore, we have:
I⋅L⋅B=mgsin(60∘)
- Given:
- Mass m=10g=10×10−3kg
- Length L=10cm=10×10−2m
- Current I=1.73A
- g≈10m/s2
- sin(60∘)=√32
1.73⋅(10×10−2)⋅B=(10×10−3)⋅10⋅√32
- This simplifies to:
1.73⋅10−1⋅B=5√3×10−3
- Rearranging gives:
B=5√3×10−31.73×10−1
- Calculating the right-hand side:
B=5√31.73×10−2
- Approximating √3≈1.732:
B≈5×1.7321.73×10−2≈5×10−2≈0.05T
- Thus, the value of B for which the rod remains stationary on the inclined plane is approximately 1T.
Similar Questions
A block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA metallic rod of mass per unit length 0.5kgm−1 is lying horizontally on a straght inclined plane which makes an angle of 30∘ with the horizontal. The rod is not allowed to slide down by flowing a current throguh it when a magnetic field of induction 0.25T is acting on it in the vertical direction. The current flowing in the rod to keep it stationary is
View SolutionA projectile is projected with speed u at an angle of 60∘ with horizontal from the foot of an inclined plane. If the projectile hits the inclined plane horizontally, the range on inclined plane will be.
View SolutionA block is placed on a smooth inclined plane as shown . For what value of horizontal force F, the block will remain at rest ?

View SolutionA body is placed on a smooth inclined plane of inclination 1 in x. The horizontal acceleration to be given to the inclined plane so that the body on it remains at rest with respect to inclined plane is
View SolutionA rod of length 1m is sliding in a corner as shown. At an instant when the rod makes an angle of 60∘ with the horizontal plane, the velocity of point A on the rod is 1 m/s. The angular velocity of the rod at this instant is :
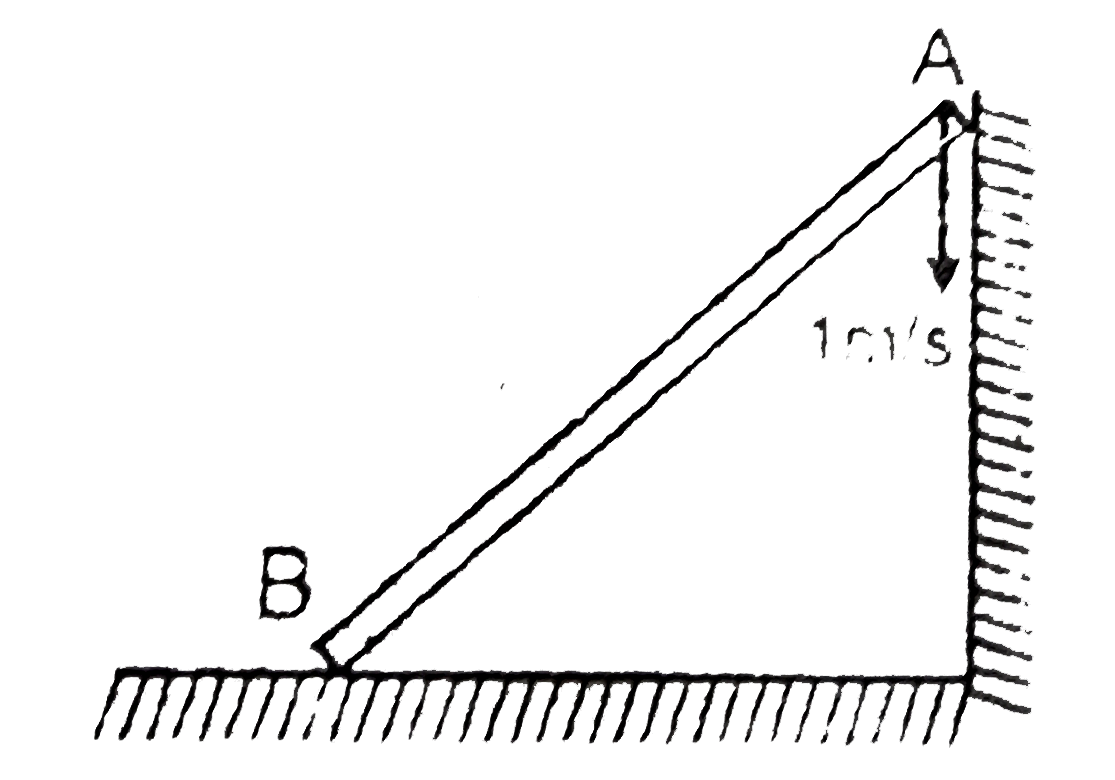
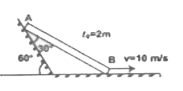
View SolutionA rod AB is placed on smooth inclined plane as shown in the figure. At the instant which is shown in the figure, the angular velocity of the rod is
View SolutionA horizontal force F is applied to a block of mass m on a smooth fixed inclined plane of inclination θ to the horizontal as shown in the figure. Resultant force on the block up the plane is:

View SolutionAn object is kept on a smooth inclined plane of height 1 unit and length l units. The horizontal acceleration to be imparted to the inclined plane so that the object is stationary relative to the incline is
View Solution
