A 2 kg mass is attached to a spring of force constant 600 N/m and rests on a smooth horizontal surface. A second mass of 1 kg slides along the surface toward the first at 6 m/s.a Find the amplitude of oscillation if the masses make a perfectly inelastic collision and remain together on the spring. What is the period of oscillation ?b Find the amplitude and period of oscillation if the collision is perfectly elastic .c For each case write down the position x as a function of time t for the mass attached to the spring assuming that the collision occurs at time t = 0 . What is the impulse given to the 2 kg mass in each case ?
From conservation of linear momentum at mean position velocity of combined mass will be 2 m/s This is the maximum velocity of combined mass.b If the collision is elastic In elastic collision This is maximum velocity.c In both cases journey is started from mean position will be the displacement-time equation.For impulse we can apply the equation.Impulse = change in linear momentum.
Related Solutions
A 2kg mass is attached to a spring of force constant 600 N//m and rests on a smooth horizontal surface. A second mass of 1kg slides along the surface toward the first at 6m//s . (a) Find the amplitude of oscillation if the masses make a perfectly inelastic collision and remain together on the spring. what is the period of oscillation ? (b) Find the amplitude and period of oscillation if the collision is perfectly elastic. ( c) For each case , write down the position x as a function of time t for the mass attached to the spring, assuming that the collision occurs at time t = 0 . What is the impulse given to the 2kg mass in each case ?
View SolutionA 2kg mass is attached to a spring of force constant 600 N//m and rests on a smooth horizontal surface. A second mass of 1kg slides along the surface toward the first at 6m//s . (a) Find the amplitude of oscillation if the masses make a perfectly inelastic collision and remain together on the spring. what is the period of oscillation ? (b) Find the amplitude and period of oscillation if the collision is perfectly elastic. ( c) For each case , write down the position x as a function of time t for the mass attached to the spring, assuming that the collision occurs at time t = 0 . What is the impulse given to the 2kg mass in each case ?
View SolutionA 1 kg mass is attached to a spring of force constant 600 N/m and rests on a smooth horizontal surface with other end of the spring tied to wall as shown in figure. A second mass of 0.5 kg slides along the surface towards the first at 3m/s. If the masses make a perfectly inelastic collision, then find amplitude and time period of oscillation of combined mass.
View SolutionA mass m attached to a spring oscillates with a period of 2 seconds. If the mass is increased by 2 kg, the period increases by one second. Find the mass m.
View SolutionThe force constant of an ideal spring is 200 Newton / m. 200 / kg on it. A mass of one mass is stirred. Find the period of oscillation.
View SolutionIn the given figure, a mass M is attached to a horizontal spring which is fixed on one side to a rigid support. The spring constant of the spring is k. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass is in equilibrium position, as shown in the figure, another mass m is gently fixed upon it. The new amplitude of oscillation will be :

View SolutionA mass M=5 kg is attached to a string as shown in the figure and held in position so that the spring remains unstretched. The spring constant is 200 Nm^(-1) . The mass M is then released and begins to undergo small oscillations. The amplitude of oscillation is
View SolutionA mass M=5 kg is attached to a string as shown in the figure and held in position so that the spring remains unstretched. The spring constant is . The mass M is then released and begins to undergo small oscillations. The amplitude of oscillation is
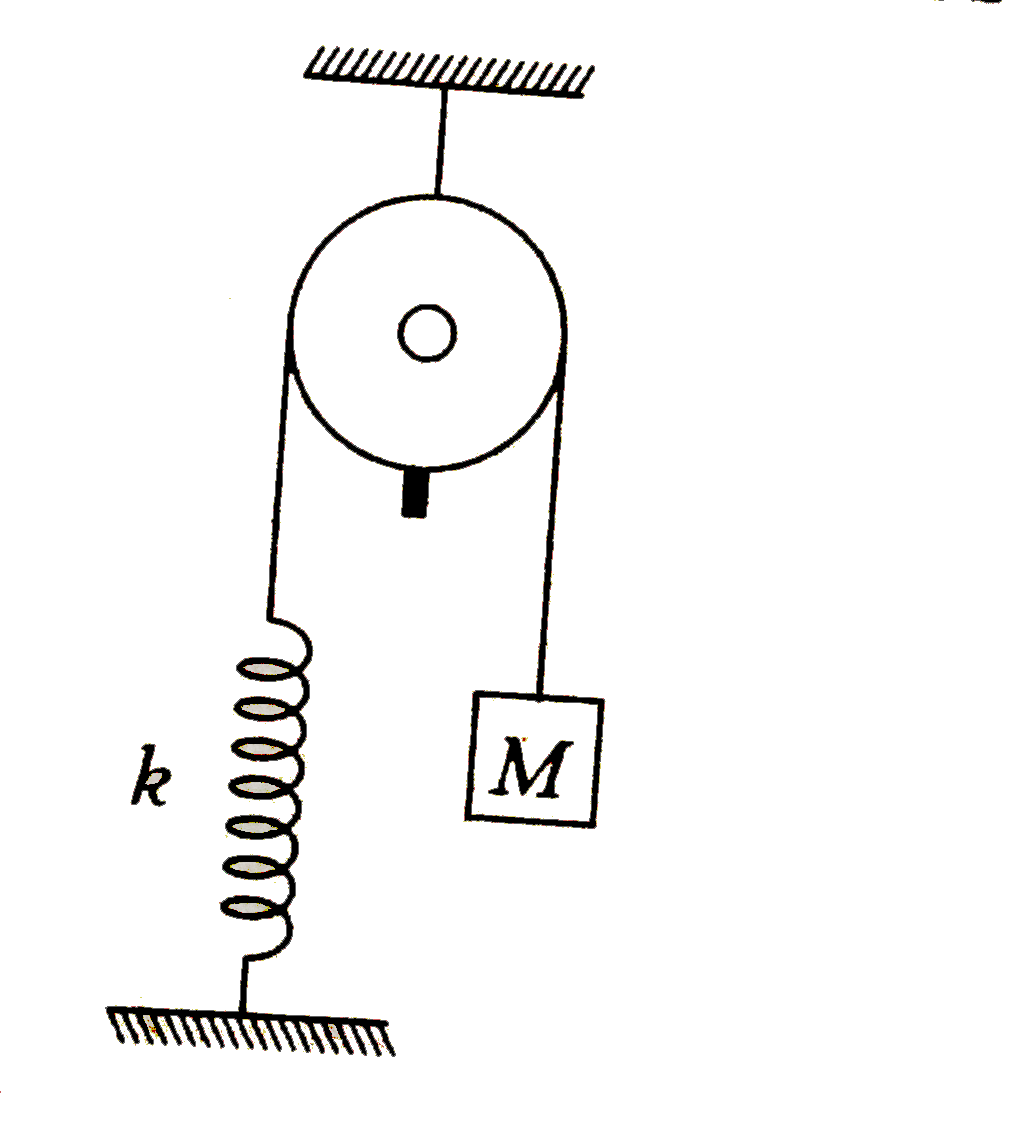
View Solutionएक स्प्रिंग से बँधा द्रव्यमान m का एक पिण्ड क्षैतिज तल में सरल आवर्ती दोलन करता है | स्प्रिंग का बल नियतांक K तथा दोलन का आयाम a है | जब पिण्ड अपनी माध्य स्थिति से होकर गुजरता है, तो द्रव्यमान m का एक अन्य पिण्ड इसके ऊपर रख दिया जाता है | ज्ञात कीजिए : ( i ) दोलनों की आवृत्ति
( ii ) दोलनों का आयाम.
View Solutionएक स्प्रिंग से जुड़ा द्रव्यमान M का पिंड,2 के आवर्तकाल के साथ दोलन करता है। यदि द्रव्यमान में 2 kg की वृद्धि की जाती है, तो आवर्तकाल एक सेकंड से बढ़ जाता है। यह मानते हुए कि हुक के नियम का पालन किया जाता है, प्रारंभिक द्रव्यमान M ( kg में ) ज्ञात कीजिए।
View SolutionA block of mass 2 kg executes SHM on a smooth horizontal plane under the action of restoring force of a spring. If the amplitude and time period of oscillation are 0.05 m and pi//5 second, the maximum force exerted by the spring on the block is
View Solutionएक आदर्श स्प्रिंग से 0.5 किग्रा द्रव्यमान के एक पिण्ड को लटकाकर ऊपर - नीचे दोलन कराया जाता है | यदि दोलन का आवर्तकाल 1.57 सेकण्ड हो, तो स्प्रिंग का बल नियतांक ज्ञात कीजिए |
View SolutionA mass M attached to a spring oscillates with a period of 2 s. If the mass is increased by 2 kg the period increases by one second. Find the initial mass M (in kg) assuming that Hooke's Law is obeyed.
View Solutionm द्रव्यमान का एक पिण्ड एक स्प्रिंग से बँधा हुआ है और दोलन करता है। यदि स्प्रिंग का बल नियतांक K हो तो पिण्ड का दोलनकाल होगा
View Solutionएक आदर्श स्प्रिंग का बल नितंक 200 न्यूटन/मीटर है । इस पर किग्रा द्रव्यमान के पिण्ड को लटकाकर दोलित कराया जाता है । पिण्ड के दोलन का आवर्तकाल ज्ञात कीजिए ।
View SolutionThe time period of an oscillating spring of mass 630 g and spring constant 100 N/m with a load of 1 kg is
View Solutionएक स्प्रिंग का बल नियतांक 200 न्यूटन/मीटर है | इससे 98 किग्रा द्रव्यमान का पिण्ड लटका है, जो सरल आवर्त गति में दोलन करता है | पिण्ड का आवर्तकाल ज्ञात कीजिए |
View SolutionWhen a mass M is attached to the spring of force constant k , then the spring stretches by . If the mass oscillates with amplitude l , what will be maximum potential energy stored in the spring
View Solution"48 N m"^(-1) A particle of mass 3 kg attached to a spring of force constant performs simple harmonic motion on a frictionless horizontal surface. The period of oscillation of the particle, in seconds, is
View SolutionA mass m attached to a light spring oscillates with a period of 2 s. If the mass is increased by 2 kg, the period increases by 1 s. Then the value of m is
View Solution