The time period of an oscillating spring of mass 630 g and spring constant 100 N/m with a load of 1 kg is
0.2πs
0.21πs
0.22πs
0.02πs
The correct Answer is:C
T=2π√1+0.633100=2π√1.21100=2π×1.110
=0.22πs
Topper's Solved these Questions
Similar Questions

The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks isView SolutionFind the time period of the oscillation of mass m in figure a,b,c what is the equivalent spring constant of the pair oif springs in each case?
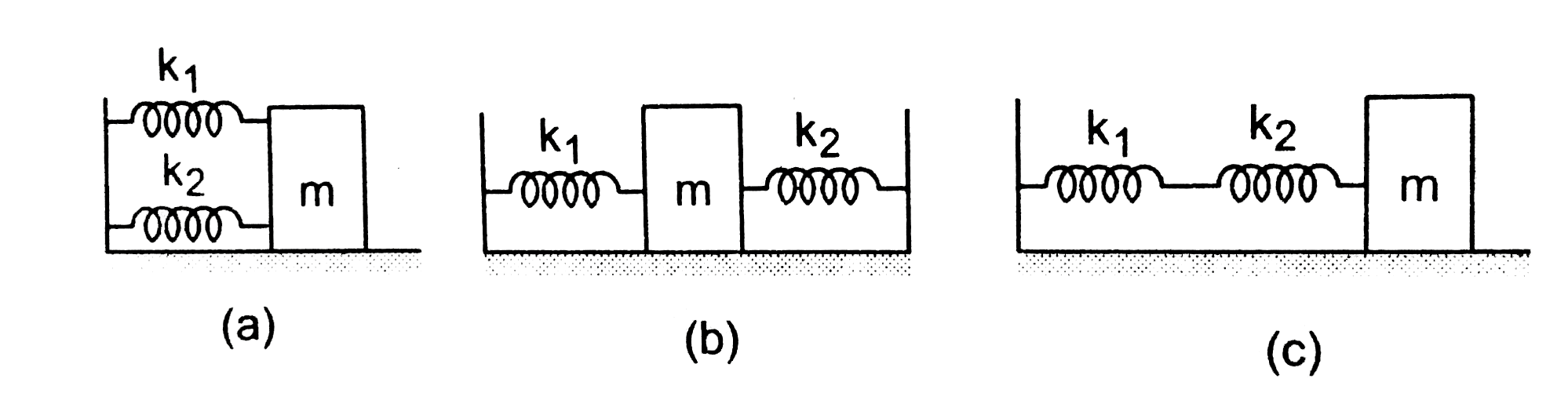 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Find the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
 A2π√mkBπ√mkC4π√mkD2π√m2k
A2π√mkBπ√mkC4π√mkD2π√m2k - Question 2 - Select One
The period of oscillation of a mass M, hanging from a spring of force constant k is T. When additional mass m is attached to the spring, the period of oscillation becomes 5T/4. m/M =
A9:16B25:16C25:9D16:9 - Question 3 - Select One
The time period of a loaded spring on earth is 6s. On the surface of moon, the time period of the same loaded spring will be
A√6sB6√6sC1sD6s
What is the oscillation amplitude of a 4.00kg box oscillating on a spring with spring constant 100N/m if at time t= 1.00s the position is x = 0.129m and the velocity is v= 5.00m/s? At t= 0, what are (a) the position and (b) the velocity?
View SolutionFind the time period of the oscilltion of mass m in figure a and b. What is the equivalent spring constant of the spring in each case. ?
 View Solution
View SolutionThe period of oscillation of a mass m suspended by an ideal spring is 2s. If an additional mass of 2 kg be suspended, the time period is increased by 1s. Find the value of m.
View SolutionA mass is suspended separately by two springs of spring constants k1 and k2 in successive order. The time periods of oscillations in the two cases are T1 and T2 respectively. If the same mass be suspended by connecting the two springs in parallel, (as shown in figure) then the time period of oscillations is T. The correct relations is
 View Solution
View SolutionA load of mass M is attached to the bottom of a spring of mass 'M/3' and spring constant 'K'. If the system is set into oscillation, the time period of oscillation is
View Solution

