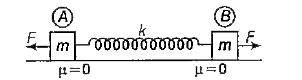
Two blocks A and B of masses m1 = 3 kg and m2 = 6 kg respectively are connected with each other by a spring of force constant k = 200 N/m as shown in the figure. Blocks are pulled away from each other by x0 = 3 cm and then released. When spring is in its natural length and blocks are moving towards each other another block C of mass m = 3 kg moving with velocity v0 = 0.4 m/s collides with A and gets stuck to it. Neglecting friction calculate a velocity v1 and v2 of the blocks A and B respectively just before collision and their angular frequency.b velocity of centre of mass of the system after collision c amplitude of oscillations of combined body d loss of energy during collision.
Angular frequencyc After collision velocity f combined blocks A + Cand velocity of block B is v2 = 0.1 m/sThe spring will compress till velocity of all the blocks becomes equal to the centre of mass. Applying conservation of mechanical energy Solving this we get A = 0.048 mor A = 4.8 cm
Related Solutions
Two blocks A and B of masses m_1 = 3 kg and m_2 = 6 kg respectively are connected with each other by a spring of force constant k = 200 N/m as shown in figure. Blocks are pulled away from each other by x_0 = 3 cm and then released. When spring is in its natural length and blocks are moving towards each other, another block of mass m 3 kg moving with velocity v_0 =0.4 m/s (towards right) collides with A and gets stuck to it. Neglecting friction, calculate (a) Velocities v_1 and v_2 of the blocks A and B respectively just before collision and their angular frequency . (b) Velocity of centre of mass of the system, after collision (c) Amplitude of oscillations of combined body (d) Loss of energy during collision.
View SolutionA block of mass 2 kg is connected with a spring of natural length 40 cm of force constant K=200 N//m . The cofficient of friction is mu=0.5 . When released from the given position, acceleration of block will be
View SolutionA block of mass 2 kg is connected with a spring of natural length 40 cm of force constant K=200 N//m . The cofficient of friction is mu=0.5 . When released from the given position, acceleration of block will be
View SolutionA block of mass 2 kg is connected with a spring of natural length 40 cm of force constant K=200 N//m . The cofficient of friction is mu=0.5 . When released from the given position, acceleration of block will be
View SolutionIn the figure shown, the system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10 N/m.
Maximum speed of the block placed horizontally is:View Solutionदो ब्लॉकों का एक निकाय किसी स्प्रिंग द्वारा जुड़ा हुआ है तथा चित्रानुसार दो समान व विपरीत बल इस पर आरोपित हैं। माना स्प्रिंग का अधिकतम खिंचाव, प्रत्येक गुटके की ओर है।
ब्लॉक B पर स्प्रिंग बल का परिमाण हैView Solution3 kg और 6 kg द्रव्यमान के दो गुटके A और B, 1800 बल नियतांक की एक द्रव्यमान रहित स्प्रिंग से जुड़े हुए हैं और फिर उन्हें एक चिकने क्षैतिज पृष्ठ पर रखा गया है। स्प्रिंग को 5 cm तक खींचने के लिए गुटकों को खींचा जाता है और फिर छोड़ दिया जाता है। जब स्प्रिंग अपनी प्राकृतिक लंबाई पर आती है, तो गुटकों का आपेक्षिक वेग ( में) क्या है?
View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:
View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:
View SolutionA block of mass is attached to a spring in natural length of spring constant . The other end of the spring is moved with a constat velocity away from the block . Find the maximum extension in the spring.
 View Solution
View SolutionA block ofmass m is attached with a spring in its natural length, of spring constant k. The other end A of spring is moved with a constant acceleration 'a' away from the block as shown in the figure -3.74 . Find the maximum extension in the spring. Assume that initially block and spring is at rest w.r.t ground frame:
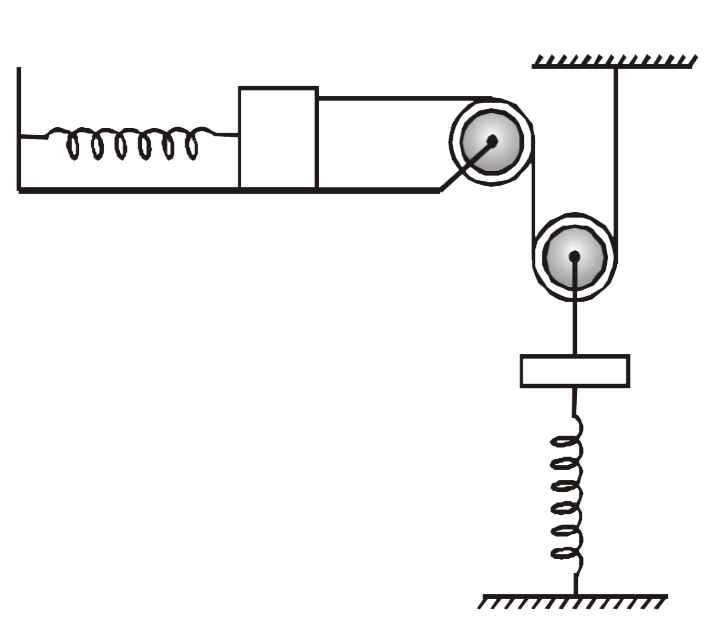
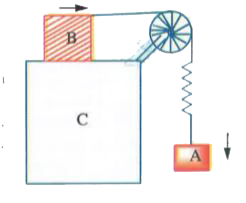
View SolutionTwo blocks A and B are connected to each other by a string and a spring, the string passes over a frictionless pulley as shown in the figure. Block B slides over the horizontal top surface of a stationary block C and the block A slides along the vertical side of C, both with the same uniform speed. The coefficient of friction between the surfaces of blocks is 0.2. Force constant of the spring is 1960 newtons/m. If mass of block A is 2 kg. The mass of block B and the energy stored in the spring are _____ kg and _____ J.
 View Solution
View SolutionThe mass of A and B blocks is 2 kg and 3 kg respectively The two blocks are placed in contact with each other on a smooth horizontal table [Figure 1.65].
View SolutionInitially spring is in its natural length . The block of mass 3 kg in contact with rigid wall . The block of mass 1 kg is pushed through a distance 4 cm towards the wall and then released. The velocity of the center of mass when the block of mass 3 kg breaks off the wall is (k = 100 N//m)
View SolutionTwo block A and B of masses m_(1) = 3kg and m_(2) = 6kg respectively are connected with each other by a spring of force constant k = 200 N//m as shown in figure. Blocks are pulled away from each other by x_(0) = 3cm and then released. When spring is in its natural length and block are moving towards each other, another block C of mass m = 3kg moving with velocity v_(0) = 0.4m//s (towards right) collides with A and gets stuck to it. Neglecting friction, calculate (a) velocity v_(1) and v_(2) of the blocks A and B respectively just before collision and their angular frequency . (b) velocity of centre of mass of the system, after collision, ( c) amplitude of oscillation of combined body, (d) loss of energy during collision.
View SolutionTwo block A and B of masses m_(1) = 3kg and m_(2) = 6kg respectively are connected with each other by a spring of force constant k = 200 N//m as shown in figure. Blocks are pulled away from each other by x_(0) = 3cm and then released. When spring is in its natural length and block are moving towards each other, another block C of mass m = 3kg moving with velocity v_(0) = 0.4m//s (towards right) collides with A and gets stuck to it. Neglecting friction, calculate (a) velocity v_(1) and v_(2) of the blocks A and B respectively just before collision and their angular frequency . (b) velocity of centre of mass of the system, after collision, ( c) amplitude of oscillation of combined body, (d) loss of energy during collision.
View SolutionA system consists of block A and B each of mass m connected by a light spring as shown in the figure with block B in contact with a wall. The block A compresses the spring by 3mg/k from natural length of spring and then released from rest. Neglect friction anywhere Acceleration of centre of mass of system comprising A and B just after A is released is
View SolutionA system consists of block A and B each of mass m connected by a light spring as shown in the figure with block B in contact with a wall. The block A compresses the spring by 3mg/k from natural length of spring and then released from rest. Neglect friction anywhere Acceleration of centre of mass of system comprising A and B just after A is released is
View SolutionTwo blocks A and B are connected to each other by a string and a spring. The string passesover a frictionless pulley as shown in the figure. Block B slides over the horizontal top surface of a stationary block C and the block A slides along the vertical side of C, both with the same uniform speed.
The coefficient of friction between the surfaces of blocks is 0.2. Force constant of the spring is 1960 N/m. If mass of block A is 2 kg. Calculate the mass of block B and the energy stored in the spring.
 View Solution
View SolutionTwo blocks A and B are standing side-by-side touching each other, on a smooth horizontal, table. Masses of "the blocks are 3 kg and 2 kg respectively. Block A is pushed towards block B with 10 N horizontal force:- How much force does block A apply on block B?
View Solution
