Two block A and B of masses m1=3kg and m2=6kg respectively are connected with each other by a spring of force constant k=200N/m as shown in figure. Blocks are pulled away from each other by x0=3cm and then released. When spring is in its natural length and block are moving towards each other, another block C of mass m=3kg moving with velocity v0=0.4m/s (towards right) collides with A and gets stuck to it. Neglecting friction, calculate
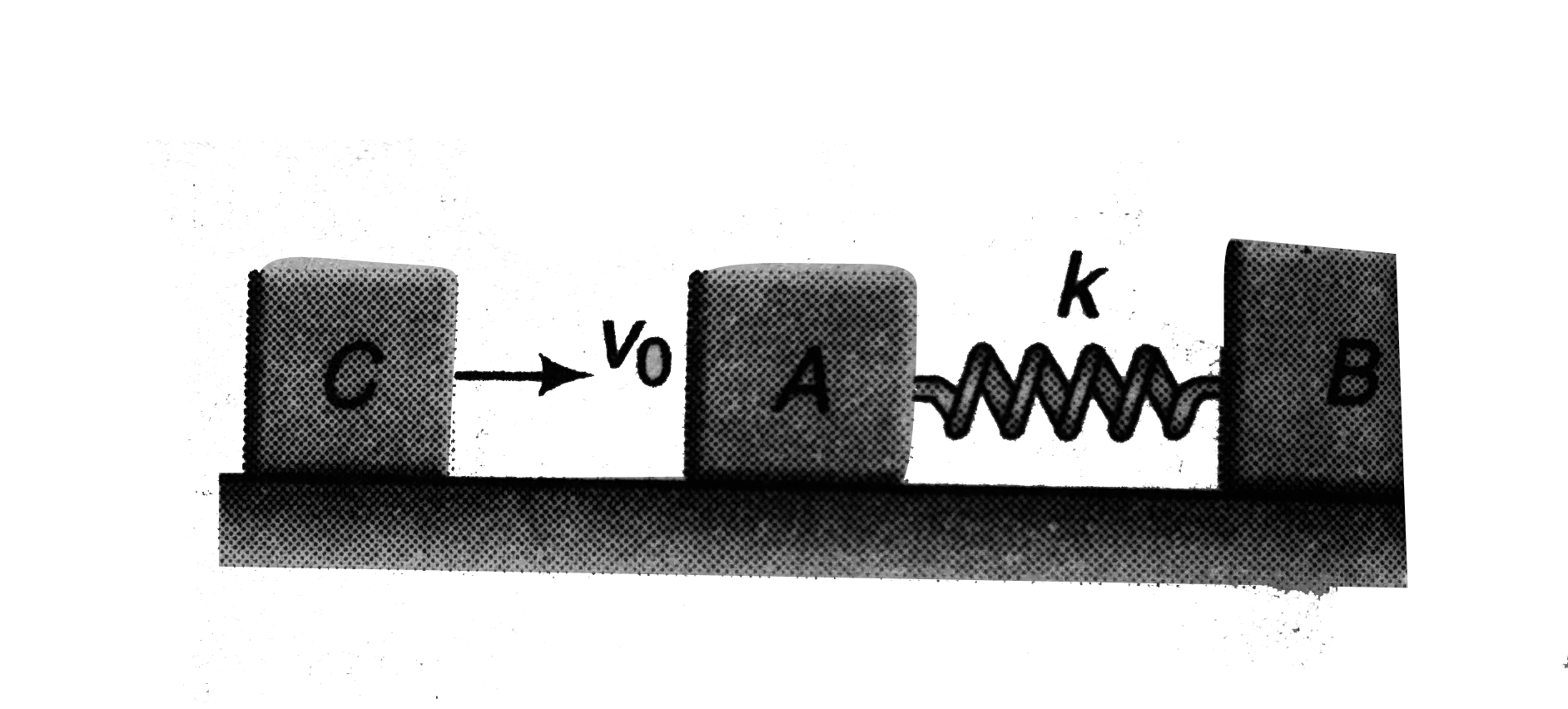
(a) velocity v1 and v2 of the blocks A and B respectively just before collision and their angular frequency .
(b) velocity of centre of mass of the system, after collision,
( c) amplitude of oscillation of combined body,
(d) loss of energy during collision.
The correct Answer is:A, B, C, D
(a) 12kx20=12μv2r
Here, μ= reduced mass =6×36+3
=2kg
∴vr=√kμx0=(√2002)(3×10−2)
=0.3m/s=2v+v
∴v=0.1m/s
∴v1=0.2m/s
and v2=0.1m/s
Angular frequency
ω=√kμ=√2002
=10rad/s

(b) vcm=m1v1+m2v2+m3v3m1+m2+m3
=(3)(0.2)−(6)(0.1)+3(0.4)3+6+3
=0.1m/s (towards right)
( c) After collision velocity of combined blocks (A+C)
v0=(3×0.2)+(3)(0.4)3+3=0.3m/s
and velocity of block B is v2=0.1m/s

The spring will compress till velocity of all the blocks equal to the centre of mass. Applying conservation of mechanical energy, 12(3+3)(0.3)2+12(6)(0.1)2=12(3+3+6)(0.1)2+12kA2
Solving this we get ,A=0.048m
or A=4.8cm
(d) ΔE=12(3)(0.4)2+12(3)(0.2)2−12(3+3)(0.3)2
=0.24+0.06−0.27=0.03J
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise 14.1
5 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Intro. Exer.
1 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Comprehension
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
Two blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View SolutionA block of mass m is suspended by different springs of force constant shown in figure.

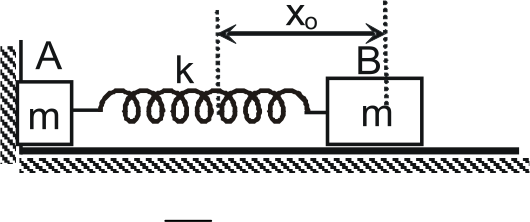
View SolutionTwo identical blocks A and B of mass m each are connected to each other by spring of spring constant k. Block B is initially shifted to a small distance x0 to the left and then released. Choose the correct statements for this problem, after the spring attains it's natural length.
View SolutionTwo blocks of masses m1=1kg and m2 = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block m1 is imparted an initial velocity v0 = 12cm/s to the right. The amplitude of oscillation is
View SolutionTwo blocks A and B of masses 3 kg and 6 kg are connected by a massless spring of force constant 1800 N m−1 and then they are placed on a smooth horizontal surface. The blocks are pulled apart to stretch the spring by 5 cm and then released. What is the relative velocity (in ms−1) of the blocks when the spring comes to its natural length?
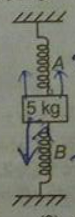
View SolutionA 5 kg block in connected with two spring A and B having force constant, K1=200Nm and K2=300Nm respectively as shown in the figure . The block is released from rest with both the springs in natural length. The maximum energy stored in the spring A will be
View SolutionA 2 kg block is connected with two springs of force constants k1=100N/m and k2=300N/m as shown in figure. The block is released from rest with the springs unstretched. The acceleration of the block in its lowest postion is (g=10m/s2)

View SolutionTwo blocks of masses 3kg and 6kg respectivley are placed on a smooth horizontal surface. They are connected by a light spring of force constant k=200N/m. Initially the spring is unstretched. The indicated velocities are imparted to the blocks. Find the maximum extension of the spring.
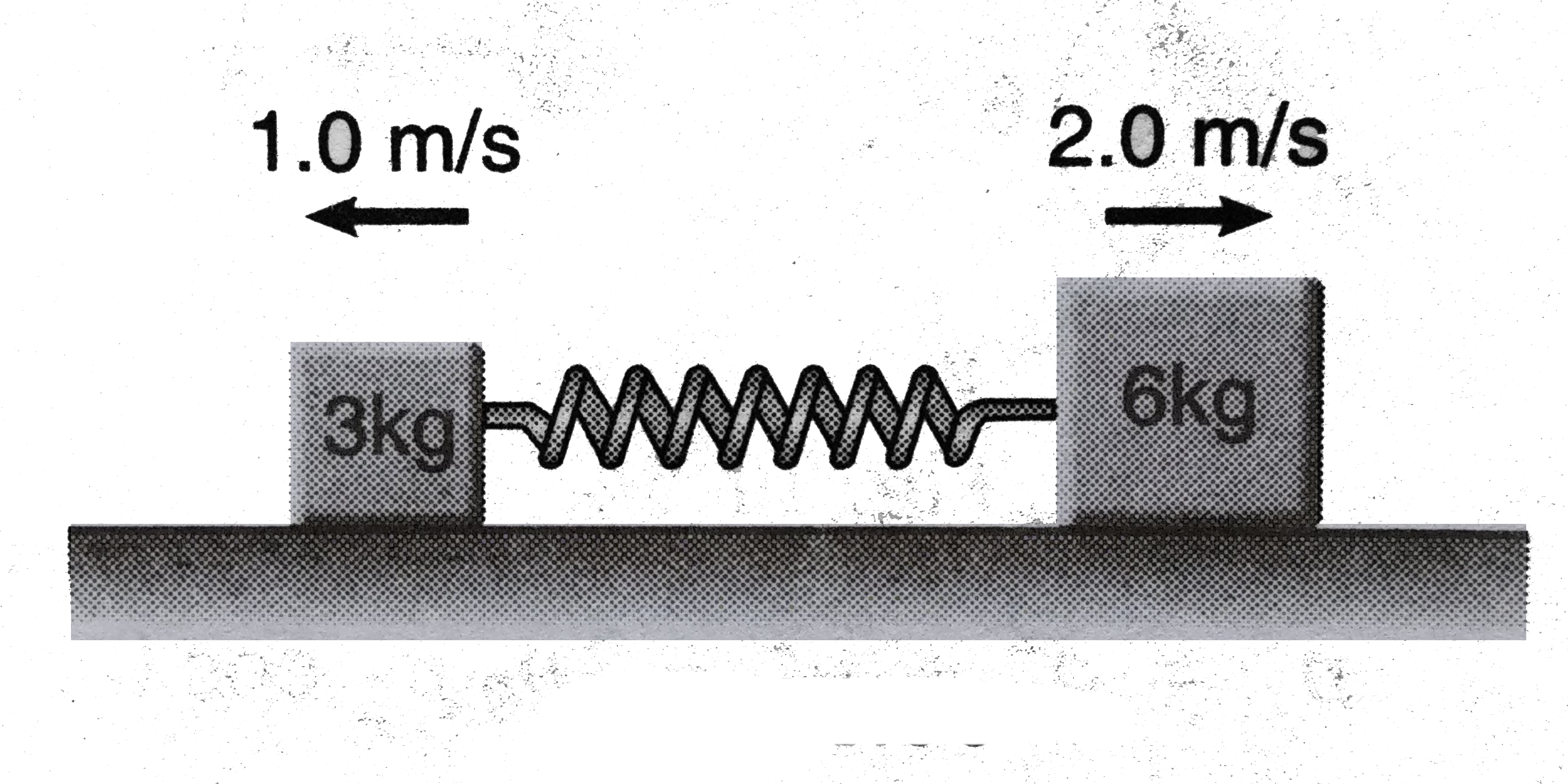
View SolutionTwo blocks of masses 3kg and 6kg respectivley are placed on a smooth horizontal surface. They are connected by a light spring of force constant k=200N/m. Initially the spring is unstretched. The indicated velocities are imparted to the blocks. Find the maximum extension of the spring.
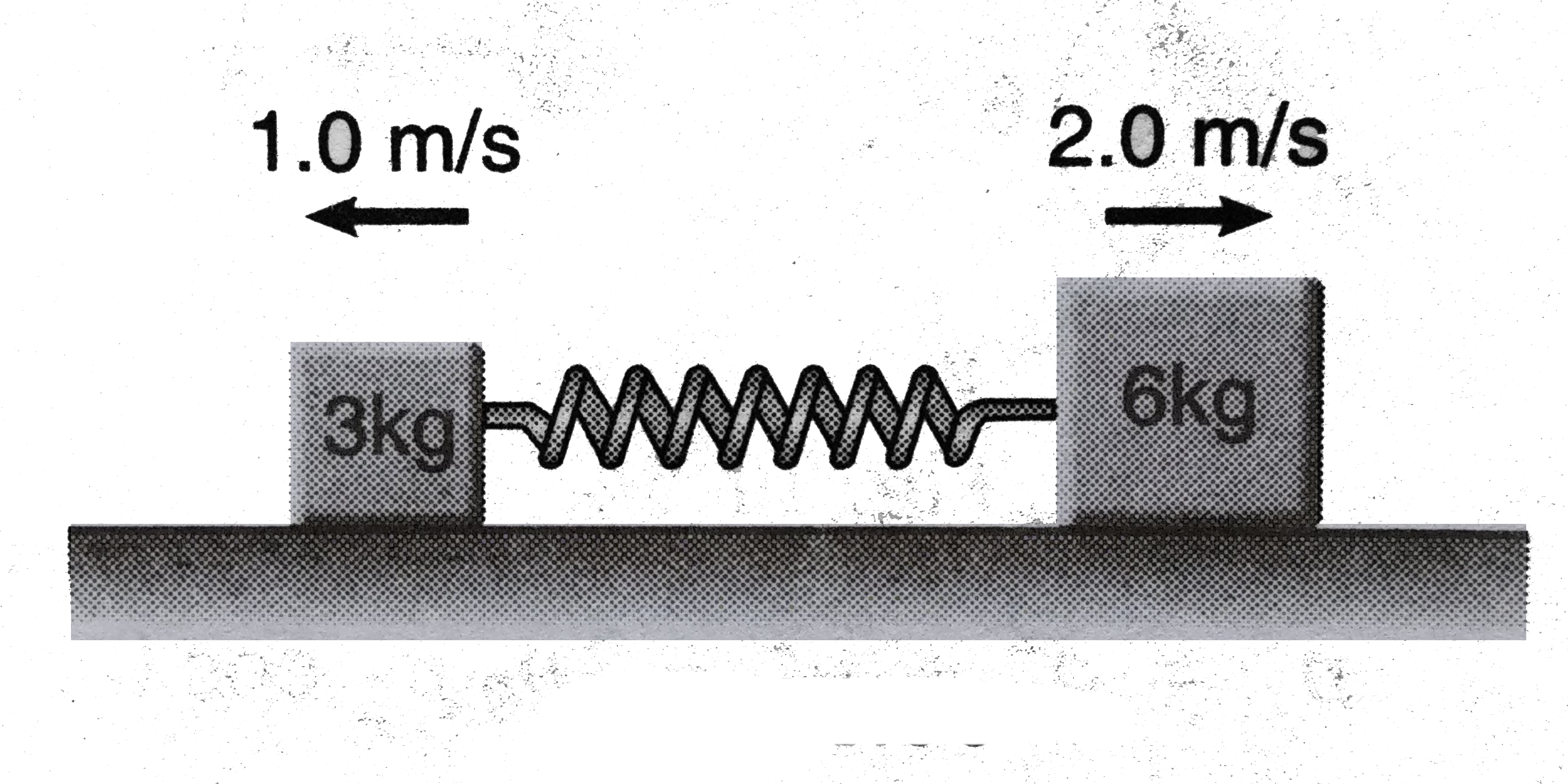
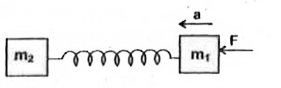
View SolutionTwo blocks of masses m1 and m2 are connected to each other with the help of a spring. If pushing force F is given to the mass m1 providing acceleration a to it, then acceleration of m2 is
View Solution
