A quadratic undeformable superconducting loop of mass m and side a lies in a horizontal plane in a nonuniform magnetic field whose induction varies in space according to the law Bx = - αx By = 0 Bz = αz + B0 Fig. 109. The inductance of the loop is L. At the initial moment the centre of the loop coincides with the origin O and its sides are parallel to the x and y-axes. The current in the loop is zero and it is released.How will it move and where will it be in time t after the beginning of motion?
The magnetic flux across the surface bounded by the superconducting loop is constant. Indeed The magnetic flux through the surface bounded by the loop is the sum of the external magnetic flux and the flux of the magnetic field produced by the current I passing through the loop. Therefore the magnetic flux across the loop at any instant isat the initial moment z = 0 and I = 0 the current I at any other instant will be determined by the relationThe resultant force exerted by the magnetic field on the current loop is the sum of the forces acting on the sides of the loop which are parallel to the y-axis i.e.and is directed along the z-axis.Therefore the equation of motion for the loop has the formThis equation is similar to the equation of vibrations of a body of mass m suspended on a spring of rigidityThis analogy shows that the loop will perform harmonic oscillations along the z-axis near the equilibrium position determined by the conditionThe frequency of these oscillations will beThe coordinate of the loop in a certain time t after the beginning of motion will be
Related Solutions
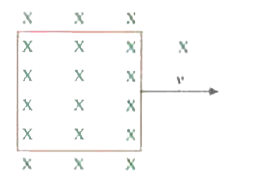
A conducting square loop of side L and resistance R moves in its to one of tis sides. A magnetic induction B , constant in time and space, pointing perpendicular to and into the plane of the loop exists every where. The current induced in the loop is
 View Solution
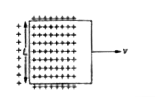
View SolutionA conducting square loop of side L and resistance R moves in its plane with a uniform velocity v perpendicular to one of its sides. A magnetic induction B constant in time and space,pointing perpendicular and into the plane at the loop exists everywhere with half the loop outside the field, as shown in fig. the induced emf is:
View SolutionA conducting square loop of side L at resistance R moves in its plane with a uniform velocity v perpendicular to one of its sides. A magnetic induction B constant in time and space, point perpendicular and into the plane at the loop exists everywhere with half the loop outside the field, as shown in Fig. The induced EMF is
 View Solution
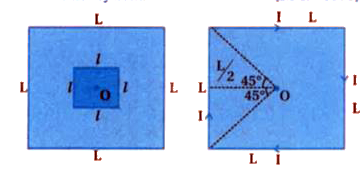
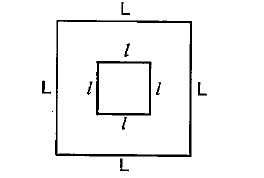
View SolutionA small square loop of wire of side l is placed inside a large square loop of wire of side . The loops are coplanar and their centres coincide. Find the mutual inductance of the system.
 View Solution
View SolutionA small square loop of wire of side l is placed inside a large square loop of wire of side L (L gt gt l) . The loops are coplanar and their centre coincide. What is the mutual inductance of the system ?
View SolutionA small square loop of wire of side l is placed outside a large (square loop) of side L. The loops are coplanar and their centres coincide. The mutual induction of the system is:
View SolutionA small square loop of wire of side l is placed inside a large square loop of side L. (L gt gt l) . The loops are coplanar and their centres coincide. The mutual induction of the system is :
View SolutionA small square loop of wire of side l is placed inside a large squar loop of wire of side L(gt gt l). The loop are coplanar and their centres coincide. What is the mutual inductance of the system?
View SolutionA small square loop of wire of side l is placed inside a large square loop of wire of side L ( > > l) . The loops are coplanar and their centres coincide. What is the mutual inductance of the system?
View SolutionA small square loop of wire of side is placed inside a large squre loop of wire of side . The loops are coplanar and their centre coincide. What is the mutual inductance of the system ?
View SolutionA small square loop of wire of side l is placed inside a large square loop of side L . The loops are coplanar and their centres coincide. Find the mutual inductance of the system.
 View Solution
View SolutionA small square loop of wire of side l is placed inside a large square loop of wire of side L(Lgtgtl) . The loops are co-planer and their centres coincide. The mutual inductance of the system is proportional to
View SolutionA small square loop of wire of side l is placed inside a large square loop of wire of side L(Lgtgtl) . The loops are coplanar and their centres coincide. Give the dependence of mutual inductance.
View SolutionA small square loop of wire of side 'I' is placed inside a large square loop of side L (L > I). If the loops are coplanar and their centres coincide, the mutual inducation of the system is directly proportional to
View SolutionA small square loop of wire of side l is placed inside a large square loop of wire of side . The loops are co-planer and their centres coincide. The mutual inductance of the system is proportional to
View SolutionA square wire loop with sides 0.5 m is placed with its plane perpendicular to the magnetic field. The resistance of the loop is . The rate at which the magnetic induction should be changed so that a current of 0.1 A is induced in the loop is
View SolutionMagnetic field induction at the centre O of a square loop of side a carrying current I as shown in figure.
View SolutionThe magnetic induction of the field at the point O of a loop with current O of a loop with current I, whose shape is illustrated below is-
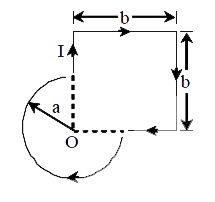 View Solution
View SolutionA small square loop of side l, L (L gt gt l) is placed inside a large square loop of the side. If the loops are coplanar and their centers coincide, then the mutual inductance of the system is directly proportional to:
View SolutionA superconducting loop of radius has self inductance . uniform & constant magnetic field is applied perpendicular to the plane of the loop. Initially current in this loop is zero. The loop is rotated about its diameter by .Find the current in the loop after rotation.
View Solution
