A superconducting loop of radius R has self inductance L.A uniform & constant magnetic field B is applied perpendicular to the plane of the loop. Initially current in this loop is zero. The loop is rotated about its diameter by 180∘.Find the current in the loop after rotation.
zero
BπR2L
2BπR2L
BπR22L
The correct Answer is:C
To solve the problem, we need to find the current induced in a superconducting loop when it is rotated by 180 degrees in a uniform magnetic field. Here’s a step-by-step solution:
Step 1: Understand the Initial Conditions
- We have a superconducting loop with radius R and self-inductance L.
- A uniform magnetic field B is applied perpendicular to the plane of the loop.
- Initially, the current in the loop is zero.
Step 2: Calculate the Initial Magnetic Flux
- The magnetic flux Φ through the loop is given by:
Φ=B⋅A
where A is the area of the loop.
- The area A of the loop is:
A=πR2
- Therefore, the initial magnetic flux Φi is:
Φi=B⋅πR2
Step 3: Consider the Final Magnetic Flux After Rotation
- When the loop is rotated by 180 degrees, the angle between the magnetic field and the area vector changes from 0∘ to 180∘.
- The final magnetic flux Φf is given by:
Φf=B⋅A⋅cos(180∘)=−B⋅πR2
Step 4: Calculate the Change in Magnetic Flux
- The change in magnetic flux ΔΦ is:
ΔΦ=Φf−Φi=−B⋅πR2−B⋅πR2=−2B⋅πR2
Step 5: Apply Faraday's Law of Electromagnetic Induction
- According to Faraday's law, the induced electromotive force (emf) E in the loop is related to the rate of change of magnetic flux:
E=−dΦdt
- Since the loop is rotated instantaneously, we can consider the induced emf to be:
E=−ΔΦ=2B⋅πR2
Step 6: Relate Induced emf to Current
- For a superconducting loop, the resistance R is zero, so the induced emf is related to the current I and the self-inductance L by:
E=LdIdt
- Since the change is instantaneous, we can relate the induced emf directly to the current:
E=LI
Step 7: Solve for the Induced Current
- Setting the two expressions for emf equal gives:
LI=2B⋅πR2
- Solving for the current I:
I=2B⋅πR2L
Final Answer
The current in the loop after rotation is:
I=2B⋅πR2L
- We have a superconducting loop with radius R and self-inductance L.
- A uniform magnetic field B is applied perpendicular to the plane of the loop.
- Initially, the current in the loop is zero.
- The magnetic flux Φ through the loop is given by:
Φ=B⋅A
where A is the area of the loop.
- The area A of the loop is:
A=πR2
- Therefore, the initial magnetic flux Φi is:
Φi=B⋅πR2
- When the loop is rotated by 180 degrees, the angle between the magnetic field and the area vector changes from 0∘ to 180∘.
- The final magnetic flux Φf is given by:
Φf=B⋅A⋅cos(180∘)=−B⋅πR2
- The change in magnetic flux ΔΦ is:
ΔΦ=Φf−Φi=−B⋅πR2−B⋅πR2=−2B⋅πR2
- According to Faraday's law, the induced electromotive force (emf) E in the loop is related to the rate of change of magnetic flux:
E=−dΦdt
- Since the loop is rotated instantaneously, we can consider the induced emf to be:
E=−ΔΦ=2B⋅πR2
- For a superconducting loop, the resistance R is zero, so the induced emf is related to the current I and the self-inductance L by:
E=LdIdt
- Since the change is instantaneous, we can relate the induced emf directly to the current:
E=LI
- Setting the two expressions for emf equal gives:
LI=2B⋅πR2
- Solving for the current I:
I=2B⋅πR2L
The current in the loop after rotation is:
I=2B⋅πR2L
Similar Questions
Knowledge Check
- Question 1 - Select One
A conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
AI r BB2πrIBCzeroDπrIB
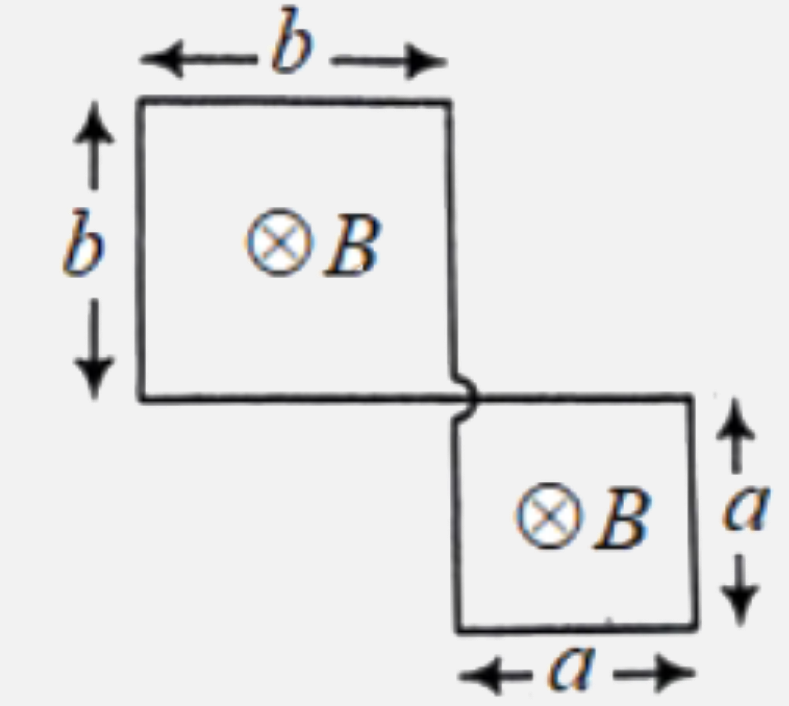
A conducting loop (as shown) has total resistance R. A uniform magnetic field B=γt is applied perpendicular to plane of the loop where γ is a constant and t is time. The induced current flowing through loop is
 View Solution
View SolutionA conducting loop (as shown) has total resistance R. A uniform magnetic field B=γt is applied perpendicular to plane of the loop where γ is constant and t is time. The induced current flowing through loop is
 View Solution
View SolutionA loop of radius R and mass m is placed in a uniform magnetic field B with its plane perpendicular to the field. Current I is flowing in it. Now loop is slightly rotated about its diameter and released. Find time period of oscillation.
View SolutionA circular loop of wire is carring a current i (as shown in the figure). On applying a uniform magnetic field inward perpendicular to the plane of the loop, the loop
 View Solution
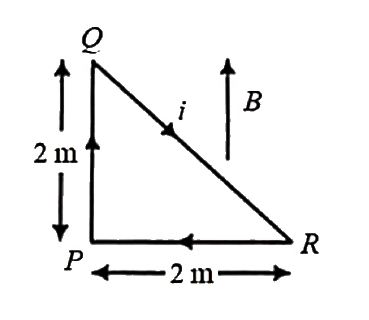
View SolutionA loop PQR carries a current i=2A as shown in the figure. A uniform magnetic field B = 2T exists in space parallel to the plane of the loop . The magnetic torque on the loop is
 View Solution
View SolutionA conducting circular loop of radiius r carries a constant current i. It is placed in a uniform magnetic field →B0 such that →B0 is perpendicular to the plane of the loop . The magnetic force acting on the loop is
View SolutionA conducting square loop of side l and resistance R moves in its plane with a uniform velocity v perpendicular ot one of its sides. A uniform and constant magnetic field B exists along the perpendicualr ot the plane of the loop as shown in . The current induced in the loop is
 View Solution
View Solution


