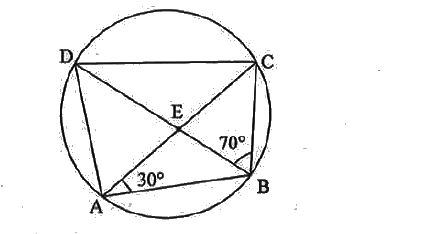
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 700 ∠BAC is 300 find ∠BCD. Further if B = BC find ∠ECD.
∠CDB = ∠BAC = 300 ...i [Angles in the same segment of a circle are equal] ∠DBC = 700 ....ii In ∆BCD ∠BCD + ∠DBC + ∠CDB = 1800 [Sum of all he angles of a triangle is 1800 ] ⇒ ∠BCD + 700 + 30.0 = 1800 [Using i and ii] ⇒ ∠BCD + 1000 = 1800 ⇒ ∠BCD = 1800 - 1000 ⇒ ∠BCD = 800 ...iii In ∆ABC AB = BC ∴ ∠BCA = ∠BAC = 300 ...iv [Angles opposite to equal sides of a triangle are equal] Now ∠BCD = 800 [From iii] ⇒ ∠BCA + ∠ECD = 800 ⇒ 300 + ∠ECD = 800 ⇒ ∠ECD = 800 - 300 ⇒ ∠ECD = 500
Related Solutions
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If find Further, if AB = BC, find
 View Solution
View SolutionABCD is a cyclic quadrilateral. Its diagonals intersect at E. /_ DBC = 70 ^@ , /_ BAC = 30^@ , But /_ BCD If AB = BC, then /_ ECD Find out.
View SolutionABCD ਇੱਕ ਚੱਕਰੀ ਚਤੁਰਭੁਜ ਹੈ ਜਿਸਦੇ ਵਿਕਰਣ ਇੱਕ ਬਿੰਦੂ E ਉੱਤੇ ਕੱਟਦੇ ਹਨ। ਜੇਕਰ ਅਤੇ is ਹੋਣ ਤਾਂ, ਪਤਾ ਕਰੋ। ਫਿਰ ਜੇਕਰ AB=BC ਹੋਵੇ ਤਾਂ ਪਤਾ ਕਰੋ।
View Solutionएक चक्रीय चतुर्भुज है जिसके विकर्ण एक बिंदु E पर प्रतिच्छेद करते है । यदि और हो , तो ज्ञात कीजिए । पुन: यदि हो, तो ज्ञात कीजिए।
View SolutionIn cyclic quadrilateral ABCD. Diagonals AC and BD intersect at P. If find
View SolutionIn the given figure ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If find
 View Solution
View SolutionIn Fig 10.33, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If and , find .
 View Solution
View SolutionIn the given figure ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If find
 View Solution
View SolutionABCD is a cyclic quadrilateral whose diagonals intersect at P. If , then the measure of is:
View SolutionABCD is a cyclic quadrilateral whose diagonals intersect at E. If BEA = , DBC = and BCD = , which of the following statements is true?
View SolutionABCD is a cyclic quadrilateral whose diagonals intersect at a point E. , , find . Futher, if AB = BC, find .
View SolutionIn cyclic quadrilateral ABCD , AD = BC , find :
View SolutionABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If , find .
 View Solution
View SolutionIn fig., ABCD is a cyclic quadrilatreral. If and , then find .
 View Solution
View Solutionਚਿੱਤਰ 10.33 ਵਿੱਚ, ABCD ਇੱਕ ਚੱਕਰੀ ਚਤੁਰਭੁਜ ਹੈ, ਜਿਸ ਵਿੱਚ AC ਅਤੇ BD ਵਿਕਰਣ ਹਨ । ਜੇਕਰ ਅਤੇ ਹੋਵੇ ਤਾਂ ਪਤਾ ਕਰੋ |
 View Solution
View Solutionबगल की आकृति में एक चक्रीय चतुभुर्ज है जिसके विकर्ण एक-दूसरे को P पर प्रतिच्छेद करते है। यदि और हो तो ज्ञात करें।
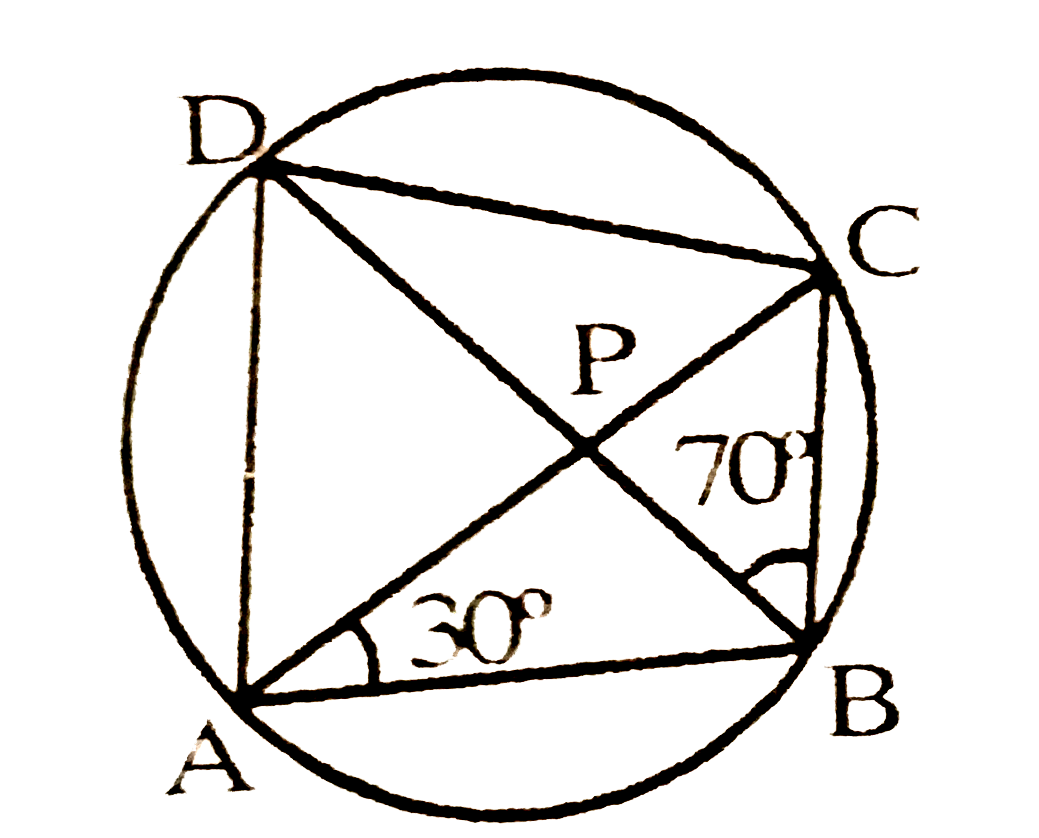 View Solution
View SolutionABCD एक चक्रीय चतुर्भुज है , जिसमे AC और BD विकर्ण है। यदि तथा हो, तो ज्ञात कीजिए
 View Solution
View Solutionआकृति में एक चक्रीय चतुभुर्ज है, जिसमे और BD विकर्ण है | यदि तथा हो तो ज्ञात कीजिए |
 View Solution
View SolutionABCD is a cyclic quadrilateral whose diagonals intersect each other at point O. If angleCAB=25^(@) and angleBCD=85^(@) then find angleCBD .
View SolutionABCD एक चक्रीय चतुर्भुज है जिसके विकर्ण एक बिंदु B पर प्रतिच्छेद करते है। यदि और हो, तो ज्ञात कीजिए। पुन: यदि AB = BC हो, तो ज्ञात कीजिए।
View Solution
