ABCD is a cyclic quadrilateral whose diagonals intersect at E. If ∠BEA = 80∘, ∠DBC = 60∘ and ∠BCD = 40∘, which of the following statements is true?
BD bisects ∠ADC
AB=BC
DA=DC
AC bisects ∠BCD
The correct Answer is:D
To solve the problem, we will analyze the given angles in the cyclic quadrilateral ABCD and determine which statement is true based on the properties of cyclic quadrilaterals and the angles formed by the intersecting diagonals.
1. Identify the Given Angles:
- We have the following angles:
- ∠BEA=80∘
- ∠DBC=60∘
- ∠BCD=40∘
2. Use the Property of Cyclic Quadrilaterals:
- In a cyclic quadrilateral, opposite angles are supplementary. Therefore, we can find ∠AEB since ∠BEA is given:
∠AEB=∠BEA=80∘
3. Determine ∠EBC:
- Since ∠DBC=60∘ and ∠BCD=40∘, we can find ∠EBC:
∠EBC=∠DBC−∠BCD=60∘−40∘=20∘
4. Calculate ∠ECB:
- Since ∠BCD=40∘ and ∠EBC=20∘, we can find ∠ECB:
∠ECB=∠BCD−∠EBC=40∘−20∘=20∘
5. Determine ∠AEC:
- Now, we can find ∠AEC using the triangle ABE:
∠AEC=180∘−(∠BEA+∠EBC)=180∘−(80∘+20∘)=80∘
6. Conclusion:
- Now we have:
- ∠AEB=80∘
- ∠AEC=80∘
- Since ∠AEB=∠AEC, it implies that line AC bisects angle BCD.
Final Statement:
Thus, the statement that "AC bisects BCD" is true.
- We have the following angles:
- ∠BEA=80∘
- ∠DBC=60∘
- ∠BCD=40∘
- In a cyclic quadrilateral, opposite angles are supplementary. Therefore, we can find ∠AEB since ∠BEA is given:
∠AEB=∠BEA=80∘
- Since ∠DBC=60∘ and ∠BCD=40∘, we can find ∠EBC:
∠EBC=∠DBC−∠BCD=60∘−40∘=20∘
- Since ∠BCD=40∘ and ∠EBC=20∘, we can find ∠ECB:
∠ECB=∠BCD−∠EBC=40∘−20∘=20∘
- Now, we can find ∠AEC using the triangle ABE:
∠AEC=180∘−(∠BEA+∠EBC)=180∘−(80∘+20∘)=80∘
- Now we have:
- ∠AEB=80∘
- ∠AEC=80∘
- Since ∠AEB=∠AEC, it implies that line AC bisects angle BCD.
Thus, the statement that "AC bisects BCD" is true.
Topper's Solved these Questions
- PRACTICE SET BOOK - ARIHANT SSCCHAPTER - PRACTICE SET EXERCISE - PRACTICE SET-4
50 Videos
- PRACTICE SET BOOK - ARIHANT SSCCHAPTER - PRACTICE SET EXERCISE - PRACTICE SET-5
50 Videos
- PRACTICE SET BOOK - ARIHANT SSCCHAPTER - PRACTICE SET EXERCISE - PRACTICE SET-2
50 Videos
- PIPES AND CISTERNS BOOK - ARIHANT SSCCHAPTER - PIPES AND CISTERNS EXERCISE - EXERCISE HIGHER SKILL LEVEL QUESTION
17 Videos
- PROBABILITYBOOK - ARIHANT SSCCHAPTER - PROBABILITYEXERCISE - EXERCISE (LEVEL-2)
19 Videos
Similar Questions
ABCD is a cyclic quadrilateral whose diagonals intersect each other at point O. If ∠CAB=25∘ and ∠BCD=85∘ then find ∠CBD.
View SolutionABCD is a cyclic quadrilateral whose diagonals intersect at P. If AB=BC, ∠DBC=70∘ and ∠BAC=30∘, then the measure of ∠PCD is :
ABCD एक चक्रीय चतुर्भुज है जिसके विकर्ण एक-दूसरे को P पर काटते हैं | यदि AB=BC, ∠DBC=70∘ तथा ∠BAC=30∘ है, तो कोण PCD का माप क्या है ?
View Solution
Knowledge Check
ABCD is a cyclic quadrilateral whose diagonals intersect at P. If AB=BC,∠DBC=70∘and∠BAC=30∘, then the measure of ∠PCD is:
Aa) 50∘Bb) 35∘Cc) 55∘Dd) 30∘ABCD is a cyclic quadrilateral whose diagonals intersect at P. If AB=BC,∠DBC=70∘and∠BAC=30∘, then the measure of ∠PCD is :
A35∘B50∘C55∘D30∘If ABCD is a cyclic quadrilateral with ∠A=50∘,∠B=80∘ , then ∠C and ∠D are
A130∘,100∘B115∘,115∘C110∘,120∘D130∘,100∘
In fig., ABCD is a cyclic quadrilatreral. If ∠BAC=50∘ and ∠DBC=60∘, then find ∠BCD.
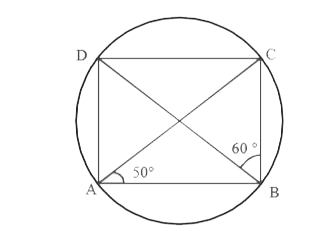
View SolutionIn cyclic quadrilateral ABCD, Diagonals AC and BD intersect at P. If ∠DBC=70∘ and ∠BAC=30∘ then find ∠BCD
View SolutionABCD is a cyclic quadrilateral of which AB is the diameter. Diagonals AC and BD intersect at E. If ∠DBC=35∘, Then ∠AED measures
View SolutionGiven that ABCD is a parallelogram whose diagonals intersect at point. O.∠ABC=110∘,∠ACB=35∘and∠ADB=55∘. The term that best describes ABCD is:
View SolutionABCD is a cycle quadrilateral. Diagonals BD and AC intersect each other at E. If ∠BEC=128∘ and ∠ECD=25∘ then what is the measure of ∠BAC ?
View Solution
