ABCD is a cyclic quadrilateral whose diagonals intersect each other at point O. If ∠CAB=25∘ and ∠BCD=85∘ then find ∠CBD.
60∘
70∘
80∘
85∘
To find the angle ∠CBD in the cyclic quadrilateral ABCD where the diagonals intersect at point O, we can follow these steps:
Step 1: Identify the given angles
We are given:
- ∠CAB=25∘
- ∠BCD=85∘
Step 2: Use the properties of cyclic quadrilaterals
In a cyclic quadrilateral, the angles subtended by the same arc are equal. Therefore, we can say that:
- ∠CAB subtends arc CB
- ∠CDB also subtends the same arc CB
Thus, we have:
∠CDB=∠CAB=25∘
Step 3: Analyze triangle DBC
In triangle DBC, we can use the fact that the sum of the angles in a triangle is 180∘:
∠DBC+∠BDC+∠DCB=180∘
Substituting the known angles:
- ∠DBC=∠CBD (which we need to find)
- ∠BDC=25∘
- ∠DCB=85∘
So we have:
∠CBD+25∘+85∘=180∘
Step 4: Solve for ∠CBD
Combine the known angles:
∠CBD+110∘=180∘
Subtract 110∘ from both sides:
∠CBD=180∘−110∘=70∘
Conclusion
Thus, the measure of ∠CBD is 70∘.
We are given:
- ∠CAB=25∘
- ∠BCD=85∘
In a cyclic quadrilateral, the angles subtended by the same arc are equal. Therefore, we can say that:
- ∠CAB subtends arc CB
- ∠CDB also subtends the same arc CB
∠CDB=∠CAB=25∘
In triangle DBC, we can use the fact that the sum of the angles in a triangle is 180∘:
∠DBC+∠BDC+∠DCB=180∘
Substituting the known angles:
- ∠DBC=∠CBD (which we need to find)
- ∠BDC=25∘
- ∠DCB=85∘
∠CBD+25∘+85∘=180∘
Combine the known angles:
∠CBD+110∘=180∘
Subtract 110∘ from both sides:
∠CBD=180∘−110∘=70∘
Thus, the measure of ∠CBD is 70∘.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the given figure, ABCD is a cyclic quadrilateral and diagonals D bisect each other at P. If ∠DBC=60∘and∠BAC=30∘, then ∠BCD is:
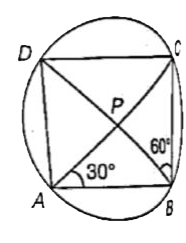 A90∘B60∘C80∘Dnone of the above
A90∘B60∘C80∘Dnone of the aboveABCD is a cycle quadrilateral. Diagonals BD and AC intersect each other at E. If ∠BEC=128∘ and ∠ECD=25∘ then what is the measure of ∠BAC ?
A52∘B103∘C93∘D98∘ABCD is a cyclic quadrilateral whose diagonals intersect at P. If AB=BC,∠DBC=70∘and∠BAC=30∘, then the measure of ∠PCD is:
Aa) 50∘Bb) 35∘Cc) 55∘Dd) 30∘
if ABCD is a trapezium, ACandBD are the diagonals intersecting each other at point Q. then AC:BD=
View SolutionABCD is a quadrilateral whose diagonals intersect each other at the point O such that OA=OB=OD.If∠OAB=30∘, then the measure of ODA is :
View SolutionABCD is a cyclic quadrilateral whose diagonals intersect at E. If ∠BEA = 80∘, ∠DBC = 60∘ and ∠BCD = 40∘, which of the following statements is true?
View SolutionABCD is a cyclic quadrilateral. Diagonals AC and BD meets at P. If ∠APB=110∘ and ∠CBD=30∘, then ∠ADB measures
View SolutionThe diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC=32∘and∠AOB=70∘, find ∠DBC.
View Solution

