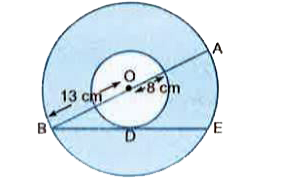
The radii of two concentric circles are 13 cm and 8 cm. AB is a diameter of the the bigger circle. BD is a tangent to the smaller circle touching it at D. Find the length AD.A 19 cmB 20 cmC 16 cmD √105 cm
The correct option is: A 19 cmExplanation:Produce BD to meet the bigger circles at E. Join AE. Then∠AEB = 90° [Angle in a semicircle]OD ⊥ BE[. BE is tangent to the smaller circle at D and OD is its radius]BD = DE [.. BE is a chord of the circle and OD ⊥ BE]. .. OD || AE [. .. ∠AEB = ∠ODB = 90°]In ΔAEB O and D are mid-points of AB and BE. Therefore by mid-Point theorem we have=> AD = 19 cm
Related Solutions
The radii of two concentric circles are 13 cm and 8 cm. AB is a diameter of the bigger circle. BD is a tangent to the smaller circle touching it at D. Find AD.
View SolutionThe radii of two concentric circle are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and the bigger circle at E. Point A is joined to D. Find the length of AD.
View SolutionIn Fig., the radii of two concentric circles are 13 cm and 8 cm. AB is diameter of the bigger circle. BD is the tangent to the smaller circle touching it at D. Find the length of AD.
View SolutionThe radii of two concentric circle are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and the bigger circle at E. Point A is joined to D. Find the length of AD.
View SolutionThe radii of two concentric circles are 13 cm and 8 cm respectively. AB is the diameter of the larger circle and BD is the tangent line of the smaller circle which touches the circle at the D point. Find the length of AD.
View SolutionThe radii of two concentric circles are 13 cm and 8 cm. AB is a diameter of the bigger circle. BD is a tangent to the smallest circle touching it at D. Find the length AD.
View Solutionदो संकेन्द्रीय वृत्तों की त्रिज्याएँ 13 सेमी और 8 सेमी है। बड़े वृत्त का व्यास AB है। छोटे वृत्त की स्पर्श रेखा BD इसे D पर स्पर्श करती है। AD की लम्बाई ज्ञात कीजिए।
View Solutionदो संकेंद्रित वृत्तों की त्रिज्याएं 12 cm और 13 cm है। AB, बड़े वृत्त का व्यास है। BD, छोटे वृत्त की स्पर्श रेखा है जो इसे बिंद D पर स्पर्श करती है। AD की लंबई (cm में) ज्ञात करें (दशमलब के एक स्थान तक सही)।
View SolutionThe radii of two concentric circles are 13 cm ad 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and the bigger circle at E. Point A is joined to D. The length of AD (in cm) is___
View SolutionThe radii of two concentric circle are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and the bigger circle at E. Point A is joined to D. Find the length of AD.
View SolutionThe radii of two concentric circles are 13cm and 8cm, AB is a diameter of bigger circle. BD is a tangent to the smaller circle touching it at D. Find the length AD.
View Solutionदो संकेन्द्रीय व्रतों कि त्रिज्याएँ 13 सेमी तथा 8 सेमी है बड़े वृत्त का व्यास AB है। BD छोटे वृत्त कि स्पर्श रेखा है जो इसे D पर स्पर्श करती है । AD की लम्बाई ज्ञात करो।
View Solutionदो संकेन्द्रीय वृत्तों की त्रिज्याये 13 सेमी और 8 सेमी है। बड़े वृत्त का एक व्यास AB है। BD छोटे वृत्त की बिन्दु D पर स्पर्श रेखा है। AD की लम्बाई ज्ञात कीजिए।
View Solutionदो संकेन्द्रीय वृत्त हैं जिनकी त्रिज्याएँ 13 सेमी तथा 5 सेमी है। बड़े वृत्त की उस जीवा की लम्बाई जो छोटे वृत्त को स्पर्श करती है, है:
View SolutionTwo concentric circles are of radii 13 cm and 5 cm. The length of the chord of the larger circle which touches the smaller circle is:
दो संकेंद्री वृत्तों की त्रिज्या 13 सेमी तथा 5 सेमी है। बड़े वृत्त की जीवा की लंबाई ज्ञात कीजिए, जो छोटे वृत्त को स्पर्श करती है।
View SolutionThe radii of two co-centric circles are 13 cm and 8 cm respectively. AB is diameter of outer circle and BE is tangent to the inner circles which touches the inner circle at point D. Then find the length of AD.
View Solutionदो संकेन्द्रीय वृत्तों की त्रिज्याये 13 सेमी और 5 सेमी है। बड़े वृत्त की उस जीवा की लम्बाई ज्ञात कीजिए जो छोटे वृत्त को स्पर्श करती है।
View SolutionTwo concentric circles with radius lengths of 13 cm and 8 cm respectively. AB is the diameter of the large circle. BD is a tangent that intersects a small circle at the point D. What is the length of AD?
View SolutionThe radii of two concentric circles are 40 cm and 41 cm What is the length of a chord of the bigger circle which is tangent to the smaller circle?
View Solutionदो संकेन्द्रीय वृत्तों की त्रिज्याएँ 5 सेमी और 3 सेमी हैं, तब बड़ें वृत्त की जीवा की लम्बाई जोकि छोटे वृत्त को स्पर्श करती है, होगी
View Solution