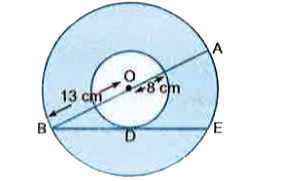
The radii of two concentric circle are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and the bigger circle at E. Point A is joined to D. Find the length of AD.
20 cm
19 cm
18 cm
17 cm
The correct Answer is:B
To find the length of AD in the given problem, we can follow these steps:
Step 1: Understand the Geometry
We have two concentric circles with radii 13 cm (larger circle) and 8 cm (smaller circle). The diameter AB of the larger circle is 26 cm (since diameter = 2 * radius). The tangent BD touches the smaller circle at point D and the larger circle at point E.
Step 2: Draw the Diagram
Draw the two concentric circles, label the center O, and mark points A and B on the larger circle. Draw the tangent line BD, touching the smaller circle at point D and the larger circle at point E.
Step 3: Identify Right Angles
Since BD is a tangent to the smaller circle at point D, it is perpendicular to the radius OD at point D. Thus, we have:
- Angle ODB = 90 degrees.
Step 4: Apply the Pythagorean Theorem
In triangle OBD, we can apply the Pythagorean theorem:
OB2=OD2+BD2
Where:
- OB=13cm (radius of the larger circle),
- OD=8cm (radius of the smaller circle).
Substituting the values:
132=82+BD2
169=64+BD2
BD2=169−64
BD2=105
Step 5: Find Length of AE
Since D is the midpoint of BE (because the radius bisects the chord), we can find AE:
- AE=2×OD=2×8=16cm.
Step 6: Apply Pythagorean Theorem in Triangle ADE
Now, in triangle ADE, we can again apply the Pythagorean theorem:
AD2=DE2+AE2
Since DE=BD (because BD is tangent to both circles), we have:
- DE2=BD2=105,
- AE2=162=256.
Substituting these values:
AD2=105+256
AD2=361
Step 7: Calculate AD
Taking the square root to find AD:
AD=√361=19cm.
Thus, the length of AD is 19 cm.
---
We have two concentric circles with radii 13 cm (larger circle) and 8 cm (smaller circle). The diameter AB of the larger circle is 26 cm (since diameter = 2 * radius). The tangent BD touches the smaller circle at point D and the larger circle at point E.
Draw the two concentric circles, label the center O, and mark points A and B on the larger circle. Draw the tangent line BD, touching the smaller circle at point D and the larger circle at point E.
Since BD is a tangent to the smaller circle at point D, it is perpendicular to the radius OD at point D. Thus, we have:
- Angle ODB = 90 degrees.
In triangle OBD, we can apply the Pythagorean theorem:
OB2=OD2+BD2
- OB=13cm (radius of the larger circle),
- OD=8cm (radius of the smaller circle).
132=82+BD2
169=64+BD2
BD2=169−64
BD2=105
Since D is the midpoint of BE (because the radius bisects the chord), we can find AE:
- AE=2×OD=2×8=16cm.
Now, in triangle ADE, we can again apply the Pythagorean theorem:
AD2=DE2+AE2
- DE2=BD2=105,
- AE2=162=256.
AD2=105+256
AD2=361
Taking the square root to find AD:
AD=√361=19cm.
Topper's Solved these Questions
Similar Questions
Find polar coordinate of (1,√3)
View SolutionIf sides of triangle are (8,b,14) then
View Solutionदो संकेन्द्रीय वृत्तों की त्रिज्या 13 सेमी तथा 8 सेमी है। AB बड़े वृत्त का व्यास तथा BD छोटे वृत्त के बिन्दु पर खींची गई स्पर्श रेखा है जो बड़े वृत्त को E पर मिलती है। बिन्दु A को बिन्दु D से मिलाया गया। AD की लम्बाई ज्ञात करे|
View SolutionThe radii of two concentric circles are 13cm and 8cm, AB is a diameter of bigger circle. BD is a tangent to the smaller circle touching it at D. Find the length AD.
View Solutionदो संकेन्द्रीय वृत्त हैं जिनकी त्रिज्याएँ 13 सेमी तथा 5 सेमी है। बड़े वृत्त की उस जीवा की लम्बाई जो छोटे वृत्त को स्पर्श करती है, है:
View Solutionदो संकेन्द्रीय व्रतों कि त्रिज्याएँ 13 सेमी तथा 8 सेमी है बड़े वृत्त का व्यास AB है। BD छोटे वृत्त कि स्पर्श रेखा है जो इसे D पर स्पर्श करती है । AD की लम्बाई ज्ञात करो।
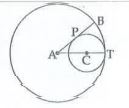
View SolutionIn the adjoining figure circles with centres A and C touch internally at point T . Line AB is tangent to the smaller circle at point P . Point B lies on the bigger circle. Radii are 16 cm and 6 cm . Find AP.
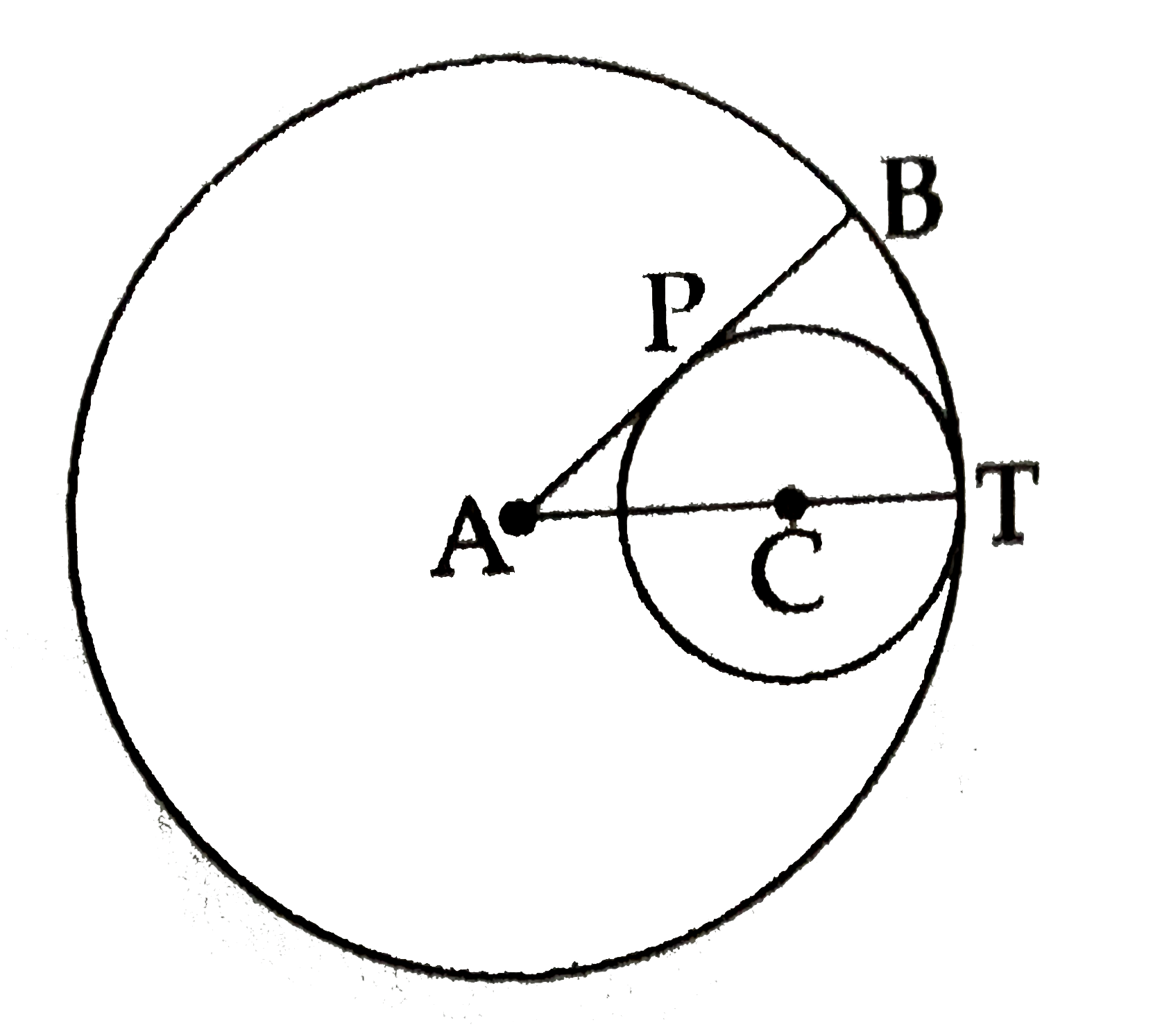
View Solutionदो संकेन्द्रीय वृत्तों की त्रिज्याएँ 13 सेमी और 8 सेमी है। बड़े वृत्त का व्यास AB है। छोटे वृत्त की स्पर्श रेखा BD इसे D पर स्पर्श करती है। AD की लम्बाई ज्ञात कीजिए।
View Solutionदो संकेन्द्रीय वृत्तों की त्रिज्याये 13 सेमी और 5 सेमी है। बड़े वृत्त की उस जीवा की लम्बाई ज्ञात कीजिए जो छोटे वृत्त को स्पर्श करती है।
View Solutionदो संकेन्द्रीय वृत्तों की त्रिज्याये 13 सेमी और 8 सेमी है। बड़े वृत्त का एक व्यास AB है। BD छोटे वृत्त की बिन्दु D पर स्पर्श रेखा है। AD की लम्बाई ज्ञात कीजिए।
View SolutionThe radii of two concentric circles are 13 cm and 8 cm respectively. AB is the diameter of the larger circle and BD is the tangent line of the smaller circle which touches the circle at the D point. Find the length of AD.
View SolutionIn Fig., the radii of two concentric circles are 13 cm and 8 cm. AB is diameter of the bigger circle. BD is the tangent to the smaller circle touching it at D. Find the length of AD.
View SolutionThe radii of two concentric circles are 13 cm and 8 cm. AB is a diameter of the bigger circle. BD is a tangent to the smaller circle touching it at D. Find AD.
View SolutionIn the adjoining figure circles with centres A and C touch internally at point T. Line AB is tangent to the smaller circle at point P. Point B lies on the bigger circle. Radii are 16 cm and 6 cm. Find AP.
View Solutionदो संकेन्द्रीय वृत्तों की त्रिज्या 13 सेमी तथा 8 सेमी है। AB बड़े वृत्त का व्यास तथा BD छोटे वृत्त के बिन्दु पर खींची गई स्पर्श रेखा है जो बड़े वृत्त को E पर मिलती है। बिन्दु A को बिन्दु D से मिलाया गया। AD की लम्बाई ज्ञात करे|
View SolutionThe radii of two concentric circle are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and the bigger circle at E. Point A is joined to D. Find the length of AD.
View Solution
