एक त्रिभुज एब्स बनाइये जिसमे BC =6 सेमि AC -'AB (b -c)=2 सेमि तथा ∠B=60∘
रचना के चरण
कोई एक किरण BX लिया। इसमें से BC =6 सेमि के काट लिया।
2. B पर ∠YBC=60∘ कोण कोण बनाया
YB को Y बिंदु तक बढ़ाया
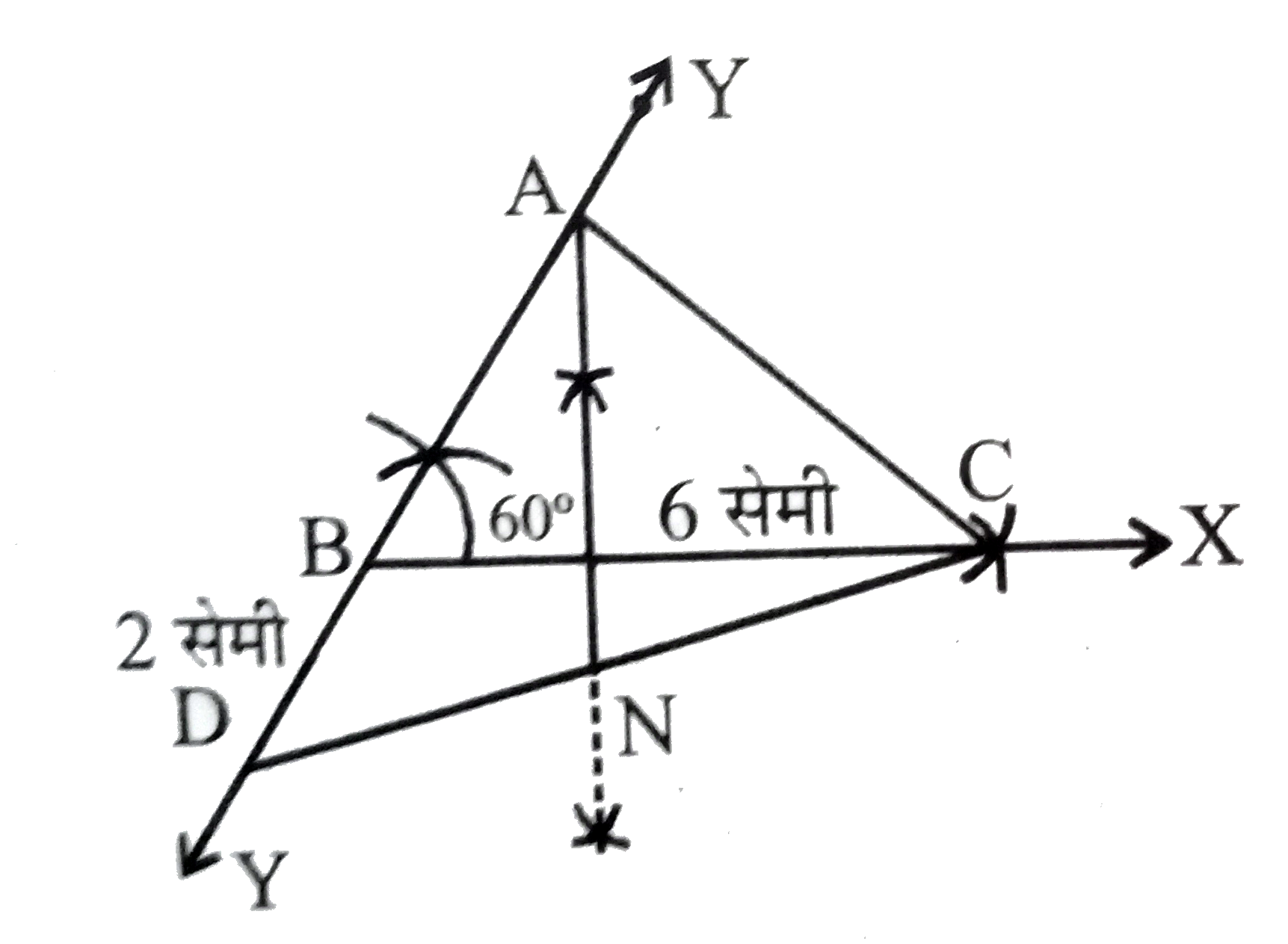
4. BY' में से BD =2 सेमि काट लिया
5. DC को मिलाया
DC के ऊपर लंबवत समद्विभाजक (perpendicular bisector) खींचा जो BY से A बिंदु पर मिलता है
7. AC को मिलाया। अंत: △ABC ही अभीष्ट त्रिभुज होगा।
Topper's Solved these Questions
Similar Questions
निम्नलिखित में से कौन-सा कथन असत्य है :-
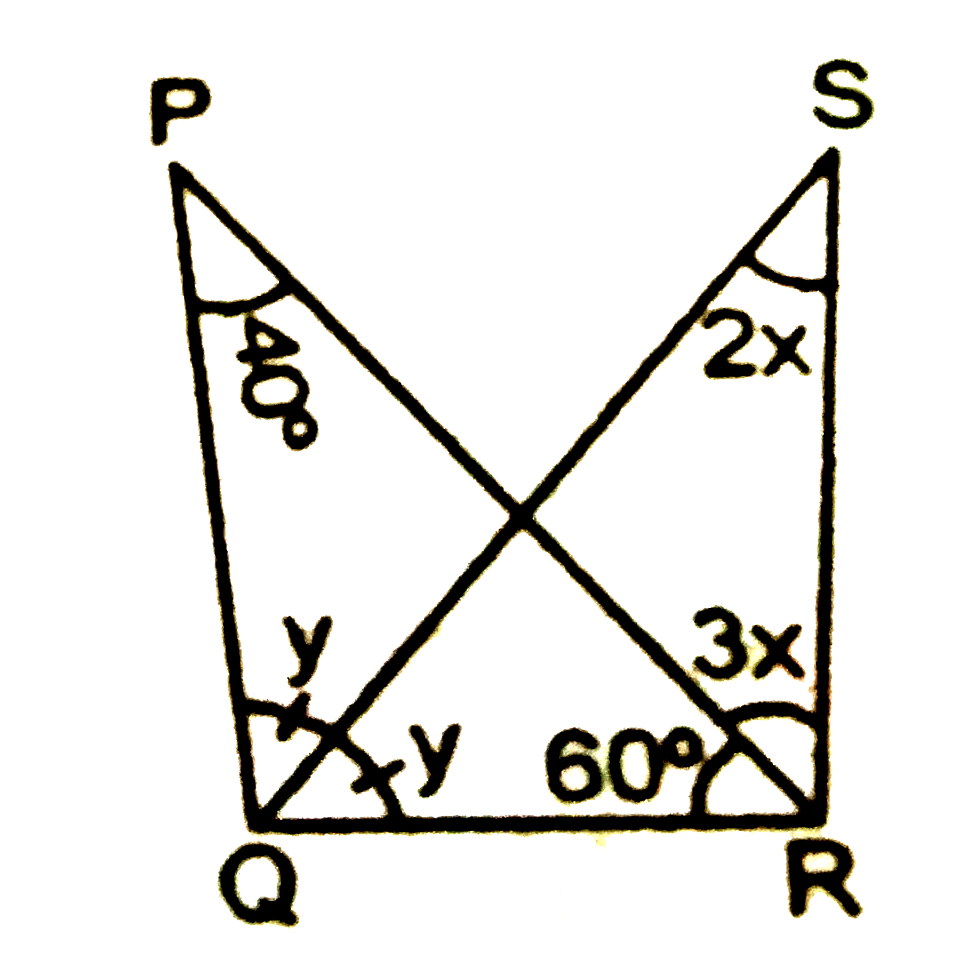
View Solutionनिम्न चित्र में x का मान है:
View SolutionProve that identities: ∣∣ ∣ ∣∣−bcb2+bcc2+bca2+ac−acc2+aca2+abb2+ab−ab∣∣ ∣ ∣∣=(ab+bc+ac)3
View SolutionConstruct a ΔABC in which BC=5cm,∠B=60∘andAC+AB=7.5cm.
View SolutionIn triangle ABC,AB=6,AC=3√6,∠B=60∘ and ∠C=45∘. Find length of side BC.
View SolutionConstruct a ΔABC in which BC=6 cm, ∠B=60∘ and (AB+AC)=9 cm. Measure AB and AC. Justify your answer.
View SolutionConstruct a ΔABC in which BC=6 cm, ∠B=60∘ and (AC−AB)=2 cm. Measure AC and AB. Justify your construction.
View Solutionयदि a,b,c में से कोई शून्य नहीं है तो दिखाएँ कि
Δ=∣∣ ∣ ∣∣−bcb2+bcc2+bca2+ac−acc2+aca2+abb2+ab−ab∣∣ ∣ ∣∣=(bc+ca+ab)3
View Solutionनिम्नलिखित दो आव्यूहों का गुणनफल निकाले । ⎡⎢⎣0c−b−c0ab−a0⎤⎥⎦तथा⎡⎢⎣a2abacabb2bcacbcc2⎤⎥⎦
View Solutionएक पुस्तकालय को एक शेल्फ में दो भिन्न प्रकार की पुस्तकें रखनी है| पुस्तकें क्रमशः 6 सेमि और 4 सेमि मोती है| तथा उसका भार क्रमशः 1 किग्रा और 112 किग्रा है| शेल्फ 96 सेमि लम्बी है तथा अधिकतम 21 किग्रा भार सेह सकती है|शेल्फ दो प्रकार की पुस्तकों से किस प्रकार भरा जाएँ ताकि उसमें अधिकतम पुस्तकें रखी जा सकें?
View SolutionCan you construct a triangle ABC with BC = 6 cm, ∠B=60∘ and AB + AC = 5cm.? If not, give reasons.
View SolutionCan you construct a triangle ABC with BC = 6 cm, ∠B=60∘ and AB + AC = 5cm.? If not, give reasons.
View SolutionCan you construct a triangle ABC with BC = 6 cm, angleB=60^(@) and AB + AC = 5cm.? If not, give reasons.
View SolutionCan you construct a triangle ABC with BC = 6 cm, ∠B=60∘ and AB + AC = 5cm.? If not, give reasons.
View SolutionIn triangle ABC,AB=6,AC=3√6,∠B=60∘ and ∠C=45∘. Find length of side BC.
View Solution
