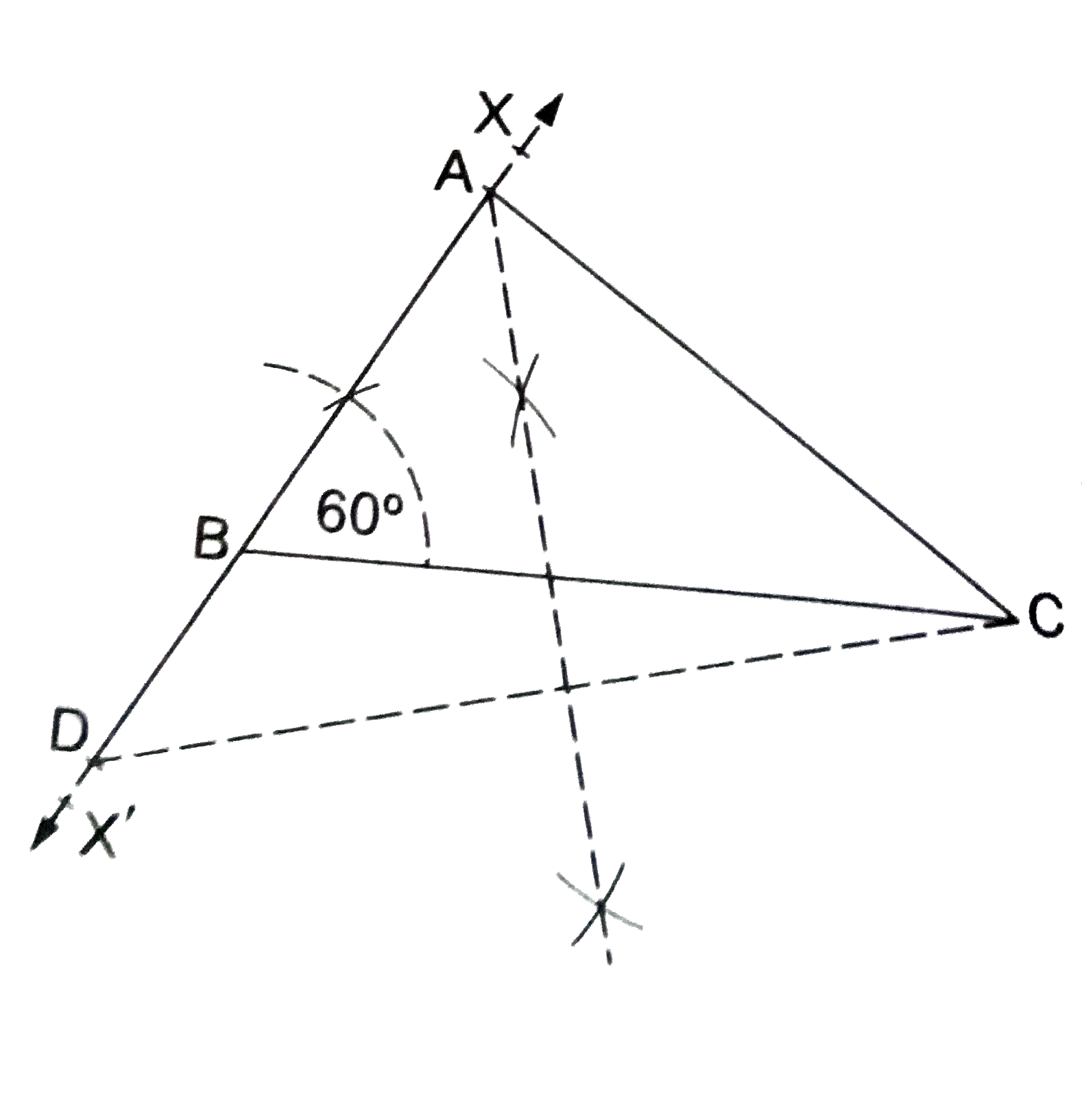
Construct a $Δ A B C$ in which $B C = 6$ cm, $∠ B = 60^{\circ}$ and $(A C - A B) = 2$ cm. Measure $A C$ and $A B$ . Justify your construction.

Video Solution

Text Solution

Verified by Experts

STEPS OF CONSTRUCTION
(i) Draw $B C = 6$ cm.
(ii) Construct $∠ C B X = 60^{\circ}$
(iii) Produce $X B$ downwards to a point $X'$ .
(iv) Set off $B D = 2$ cm along $B X'$ .
(v) Join $C D$ .
(vi) Draw the perpendicular bisector of $C D$ , meeting $B X$ at $A$ .
(vii) Join $A C$ .
Then, $Δ A B C$ is the required triangle.
Verification :
On measuring, we find that $A C = 5.4$ cm and $A B = 3.4$ cm.
$∴ (A C - A B) = (5.4 - 3.4) c m = 2$ cm.
Justification :
Since $A$ lies on the perpendicular bisector of $C D$ , we have $A D = A C$ . Now, $B D = 2$ cm $\Rightarrow A D - A B = 2$ cm
$\Rightarrow A C - A B = 2 c m [∵ A D = A C]$ .
Hence, $Δ A B C$ is the required triangle.

Updated on:21/07/2023

|

Class 9 MATHS CONSTRUCTIONS

Topper's Solved these Questions

Similar Questions

RS AGGARWAL-GEOMETRICAL CONSTRUCTIONS-Exercise 13

Home
Ask Doubt
Profile