सत्यापित करें कि त्रिघाती बहुपद के बगल में दी गई संख्यायें उनके शून्यक है | उनके शुन्यकों तथा गुणांकों के बिच के सम्बन्ध का भी सत्यापन करें |
2x3+x2−5x+2,12,1,−2
मान लें p(x)=2x3+x2−5x+2
अब, p(12)=2(12)3+(12)2−5(12)+2=2×18+14−52+2
=14+14−52+2=12−52+2=−2+2=0
पुनः p(1)=2×13+12−5×1+2=2+1−5+2=0
और p(−2)=2(−2)3+(−2)2−5(−2)+2
=2(−8)+4+10+2=−16+16=0
चूँकि p(12)=0,p(1)=0 तथा p(−2)=0, अतः 12,1,−2 त्रिघाती बहुपद p(x) के अर्थात बहुपद 2x3+x2−5x+2 के शून्यक है |
द्वितीय भाग : बहुपद 2x3+x2−5x+2 की तुलना ax3+bx2+cx+d के साथ करने पर हम पाते है कि a=2,b=1,c=−5,d=2
मान लें α=12,β=1,γ=−2
अब α+β+γ=12+1−2=12−1=−12=−ba=−x2 का गुणांकx3 का गुणांक
αβ+βγ+γα=12×1+1(−2)+(−2)×12
=12−2−1=−52=ca=x का गुणांकx3 का गुणांक
पुनः αβγ=12×1×(−2)=−1=−22=−da=−अचर पदx3 का गुणांक
Topper's Solved these Questions
- बहुपद BOOK - KC SINHACHAPTER - बहुपद EXERCISE - अभ्यास 2.1
18 Videos
- बहुपद BOOK - KC SINHACHAPTER - बहुपद EXERCISE - अभ्यास 2.2
50 Videos
- बहुपद BOOK - KC SINHACHAPTER - बहुपद EXERCISE - वस्तुनिष्ठ प्रश्न
62 Videos
- प्रायिकता या सम्भावितBOOK - KC SINHACHAPTER - प्रायिकता या सम्भावितEXERCISE - वस्तुनिष्ठ प्रश्न
54 Videos
- रचनाएँ BOOK - KC SINHACHAPTER - रचनाएँ EXERCISE - अभ्यास 11.1
14 Videos
Similar Questions
नीचे दिया गया बहुपद के आलेख को देखकर जाँच करें कि यह एक घातीय है या द्विघातीय या न तो एक घातीय है और न द्विघातीय |
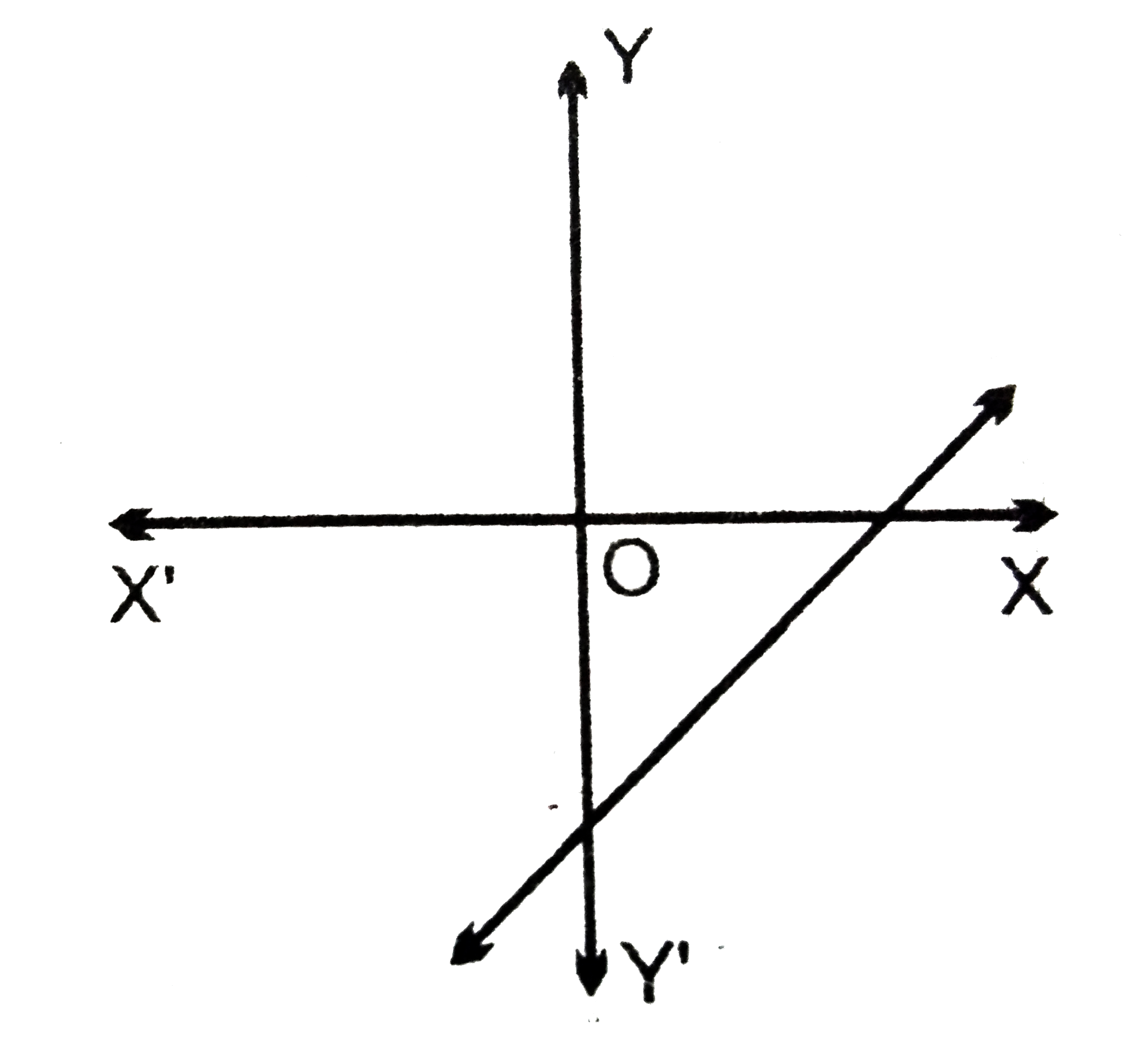
View Solutionx2−3 द्विघात बहुपद के शून्यांक ज्ञात करें और शून्यांक और गुणांक के बिच के सम्बन्ध की सत्यता की जाँच करें |
View Solutionनिम्नलिखित वंजाको में कौन बहुपद नहीं है?
View Solutionदो सिक्के उछालने में दो पट आने के प्रायिकता है:
View Solution5.6 cm लम्बा एक रेखाखण्ड खींचे और इसे 5:8 के अनुपात में अतः विभक्त करें | दोनों भागो को मापे |
View Solutionबहुपद 2x3+x2−5x+2के अन्य शून्यक ज्ञात कीजिए, यदि इसके दो शून्यक 1 और-2 हैं। ज्ञात कीजिए,
View Solutionद्विघात बहुपद x2+3x−(a+2)(a−1)के शून्यक हैं :,
View SolutionBoards 2021|बहुपद#!#किसी बहुपद के शून्यांको तथा गुणांकों में सम्बन्ध#!#Quiz की सहायता Concept का Revision#!#Topic Wise Revision
View Solutionबहुपद|बहुपदों के प्रकार|बहुपद के शून्यक|NCERT प्रश्नावली 2 .1|सारांश
View Solutionबहुपद|बहुपदों के प्रकार|बहुपद के शून्यक|बहुपद के शून्यक का जयमितीय अर्थ|अभ्यास कार्य|सारांश
View Solutionबहुपद|बहुपद के प्रकार|शून्यक|किसी बहुपद के शून्यकों और गुणांकों में सम्बन्ध|अभ्यास कार्य|सारांश
View Solutionबहुपद|बहुपदो के प्रकार|बहुपद के शून्यक|बहुपद के शून्यक का ज्यामितीय अर्थ|किसी बहुपद के शून्यांको और गुणांकों में संबंध|बहुपदो के लिए विभाजन एल्गोरिथ्म|अभ्यास कार्य|सारांश
View Solutionबहुपद के शून्यक#!#शून्यक के ज्यामितीय रूप
View Solutionबहुपद#!#किसी बहुपद के शून्यको और गुणांकों में सम्बन्ध
View Solutionबहुपद#!#बहुपद के शून्यकों तथा गुणांकों मे संबंध #!#भाग -2
View SolutionThe ratio of the sum of the salaries of A and B to the difference of their salaries is 11 : 1. The ratio of the sum of the salaries of B and C to the difference of their salaries is also 11 : 1. If A’s salary is the highest and C’s is the lowest then what is B’s salary (in Rs), given that the total of their salaries is Rs18,200?
A और B के वेतन के योग तथा उनके वेतन के अंतर में 11 : 1 का अनुपात है |B और C के वेतन के योग तथा उनके वेतन के अंतर में भी 11 : 1 का ही अनुपात है | यदि A का वेतन सर्वाधिक तथा C का वेतन सबसे कम है, तो B का वेतन ज्ञात करें जब यह दिया हुआ है कि उनके वेतनों का योग 18200 रुपये है |
View Solution
