यदि द्विघात बहुपद x2−5x+4, के शून्यांक α और β हो, तो एक द्विघात बहुपद को ज्ञात करें जिसके शून्यांक α+1β और β+1α है |
चूँकि द्विघात बहुपद x2−5x+4 के शून्यांक α और β है,
∴ α+β=5 तथा αβ=4
मान ले α'=α+1β और β'=β+1α
अब, α'+β'=α+1β+β+1α=α+β+1β+1α
=α+β+α+βαβ=5+54=254
और α'β'=(α+1β)(β+1α)=(αβ+1β)(αβ+1α)
=(αβ+1)2αβ=(4+1)24=254
अब, α' और β' शून्यांक वाला एक द्विघात बहुपद है : x2−(α'+β')x+α'β'
या, x2−254x+254
या, 4x2−25x+25 [4 से गुणा करने पर]
Topper's Solved these Questions
- बहुपद BOOK - KC SINHACHAPTER - बहुपद EXERCISE - अभ्यास 2.1
18 Videos
- बहुपद BOOK - KC SINHACHAPTER - बहुपद EXERCISE - अभ्यास 2.2
50 Videos
- बहुपद BOOK - KC SINHACHAPTER - बहुपद EXERCISE - वस्तुनिष्ठ प्रश्न
62 Videos
- प्रायिकता या सम्भावितBOOK - KC SINHACHAPTER - प्रायिकता या सम्भावितEXERCISE - वस्तुनिष्ठ प्रश्न
54 Videos
- रचनाएँ BOOK - KC SINHACHAPTER - रचनाएँ EXERCISE - अभ्यास 11.1
14 Videos
Similar Questions
नीचे दिया गया बहुपद के आलेख को देखकर जाँच करें कि यह एक घातीय है या द्विघातीय या न तो एक घातीय है और न द्विघातीय |
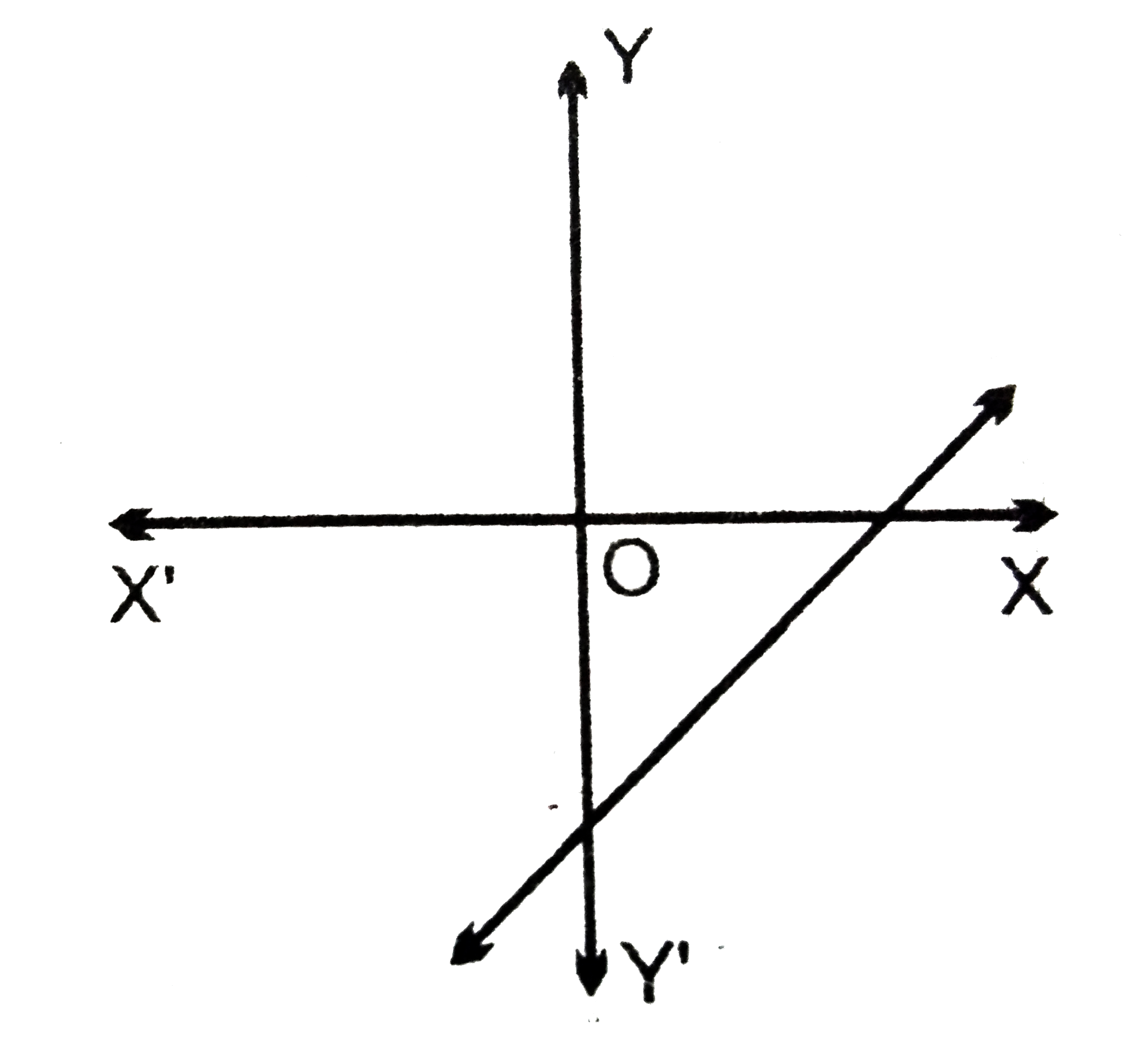
View Solutionx2−3 द्विघात बहुपद के शून्यांक ज्ञात करें और शून्यांक और गुणांक के बिच के सम्बन्ध की सत्यता की जाँच करें |
View Solutionनिम्नलिखित वंजाको में कौन बहुपद नहीं है?
View Solutionदो सिक्के उछालने में दो पट आने के प्रायिकता है:
View Solution5.6 cm लम्बा एक रेखाखण्ड खींचे और इसे 5:8 के अनुपात में अतः विभक्त करें | दोनों भागो को मापे |
View Solutionयदि बहुपद 2x2−3x+1 के शून्यांक α और β हो, तो αβ+βα के मान बताएँ :
View Solutionयदि द्विघात बहुपद x2+5x+4 के शून्यांक α और β हो, तो 1α+1β के मान ज्ञात करें :
View Solutionयदि द्विघात बहुपद x2+5x+4 के शून्यांक α और β हो, तो α−β के मान ज्ञात करें :
View Solutionयदि →a और →b असंरेख है ,तो x का मान ज्ञात कीजिए| जिसके लिए सदिश α=(2x+1)→a−→b और β=(x−2)→a+→b संरेख है
View Solutionअल्फा बीटा, और गामा किरणोंकोक्याकहाजाताहै? अल्फा-, बीटा−औरगामा किरणों के गुणों का वर्णन करते हैं
View Solutionयदि समीकरण x2−2x+2=0 के मूल α तथा β हैं, तो n का न्यूनतम मान, जिसके लिए (αβ)n=1 है
View Solutionएक ऐसा करे युग्म (α,β) जिसके लिए रैखिक समीकरण निकाय
(1+α)x+βy+z=2
αx+(1+β)y+z=3
αx+βy+2z=2 का एकमात्र एक हल है, है
View Solutionयदि समीकरण 3x2−6x+5=0 के मूल α,β हो, तो वह समीकरण जिसके मूल α+β व् 2α+β है, होगा
View Solutionयदि α,β समीकरण x2−3x+1=0 के मूल, हो तो वह समीकरण जिसके 1α−2,1β−2 मूल है, होगी।
View Solutionयदि α,β द्विघात समीकरण x2+px+p3=0(p≠0) के मूल हो तथा (α,β) परवलय y2=x पर स्थित एक बिंदु हो, तो समीकरण के मूल होगा
View Solution
