यदि G,ΔABC का केन्द्रक है और O,ΔABC के तल में कोई दूसरा बिन्दु है | तब सिध्द करे की OA2+OB2+OC2=GA2+GB2+GC2+3GO2
मान ले के G मूल बिन्दु है और GO , x - अक्ष है
माना की O≡(α,0),A≡(x1,y1),B≡(x2y2) और C≡(x3,y3)
अब बाया पक्ष OA2+OB2+OC2
=(x1−α)2+y21+(x2−α)2+y22+(x3−α)2+y23
=x21+x22+x23+y1+y22+y23+3α2−2α(x1+x2+x3)
=x21+x22+x23+y21+y22+y23+3α2 [∵x1+x2+x33=G का x - निर्देशाक =0]
पुन : दाया पक्ष =GA2+GB2+GC2+3GO2=x21+y21+x22+x23+y23+3α2
∴ बायाँ पक्ष = दाया पक्ष
Note : यहाँ हमने मूल बिन्दु G को माना है क्योकि इससे गणना सरल हो जाती है |
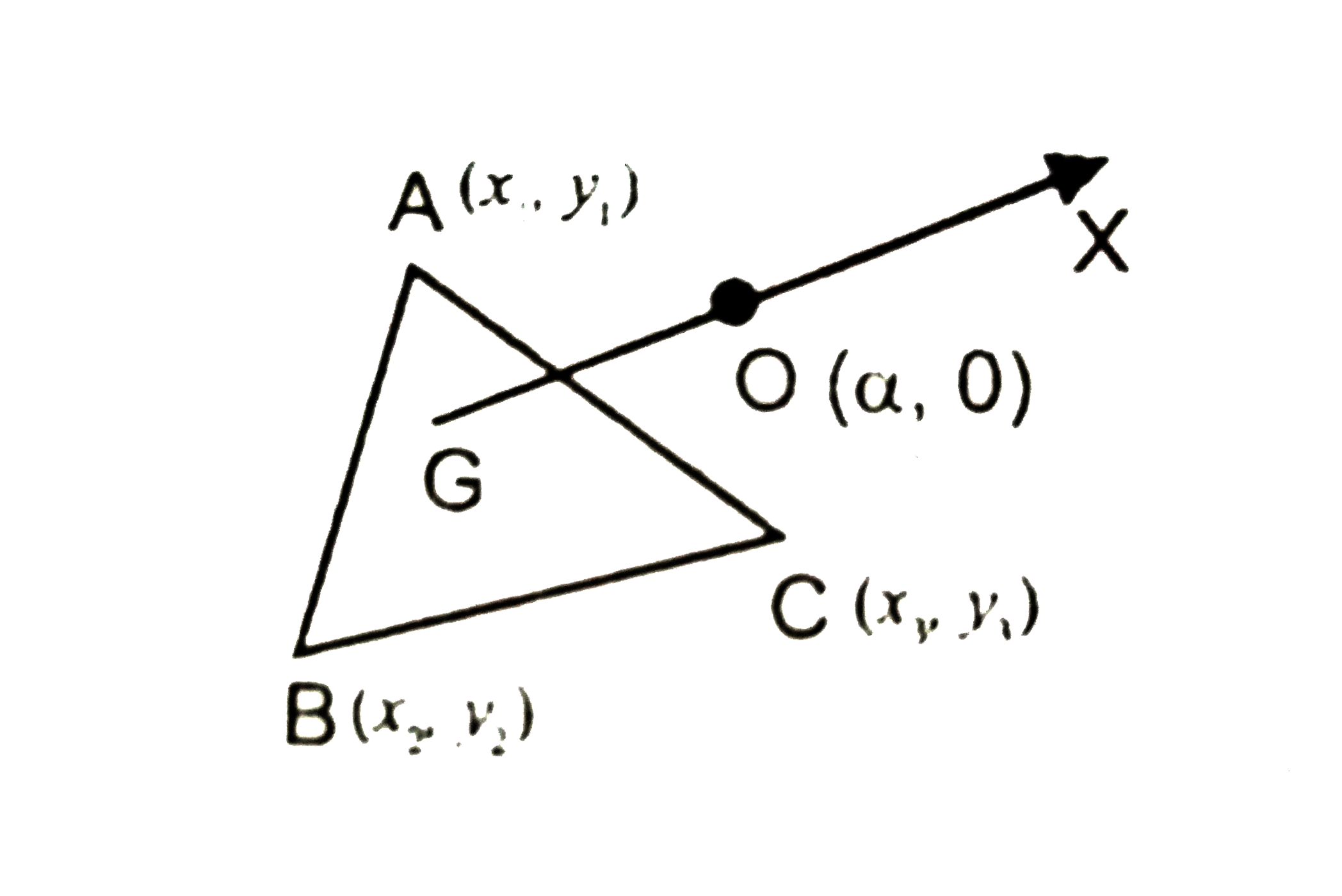
Topper's Solved these Questions
- निर्देशांक ज्यामिति Book:KC SINHAChapter:निर्देशांक ज्यामिति Exercise:प्रश्नावली 7.1 (अतिलघु उत्तरीय प्रश्न )
Explore 13 Videos
- निर्देशांक ज्यामिति Book:KC SINHAChapter:निर्देशांक ज्यामिति Exercise:प्रश्नावली 7.1 (लघु उत्तरीय प्रश्न )
Explore 5 Videos
- द्विघात समीकरण Book:KC SINHAChapter:द्विघात समीकरण Exercise:वस्तुनिष्ट प्रशन
Explore 37 Videos
- पृष्ठीय क्षेत्रफल और आयतन Book:KC SINHAChapter:पृष्ठीय क्षेत्रफल और आयतन Exercise:वस्तुनिष्ट प्रश्न(Objective Questions)
Explore 30 Videos
Similar Questions
निम्नलिखित बिन्दुए किस चतुर्थेाश में स्थित है |
(10,−3)
View Solutionयदि किसी आयत के तीन शीर्ष (−2,0),(2,0),(2,1) है तो चौथे शीर्ष के नियामक ज्ञात कीजिए |
View Solutionयदि a और b समीकरण x2−ax+b=0 के मूल है तब
View Solutionएक खोखला धातुई गोला जिसकी बाह्य त्रिज्या 6cm और अन्तः त्रिज्या 4cm है को पिघलाया जाता है और इसे एक शंकु जिसके आधार की त्रिज्या 6cm है, के रूप में ढाला जाता है, तो शंकु की ऊँचाई है:
View SolutionIf G be the centroid of the Delta ABC, then prove that AB^(2)+BC^(2)+CA^(2)=3(GA^(2)+GB^(2)+GC^(2))
View SolutionIf G be the centroid of a triangle ABC, prove that, AB2+BC2+CA2=3(GA2+GB2+GC2)
View SolutionIf G be the centroid of the ΔABCandO be any other point in theplane of the triangle ABC, then prove that: OA2+OB2+OC2=GA2+GB2+GB2+GC2+3GO2
View Solutionमाना त्रिभुज ABC का केन्द्रक G है|तब सिद्ध कीजिये की
AB2+BC2+CA2=3(GA2+GB2+GC2)
View Solutionमाना △ABC का केन्द्रक G है तथा △ABC के समतल में O कोई दूसरा बिद्नु हो तो सिद्ध कीजिए-
OA2+OB2+OC2=GA2+GB2+GC2+3GO2
View SolutionIf G is the centroid of a ΔABC, then GA2+GB2+GC2 is equal to
View SolutionIf G is the centroid of △ABC and O is any point in the plane of △ABC, show that
(1) ¯¯¯¯¯¯GA+¯¯¯¯¯¯GB+¯¯¯¯¯¯GC=¯0
(2) ¯¯¯¯¯¯OA+¯¯¯¯¯¯OB+¯¯¯¯¯¯OC=3¯¯¯¯¯¯OG.
View Solutionयदि ΔABC का केंद्रक G हो तो O इसके तल में कोई बिंदु है तो साबित करेंकि OA2+OB2+OC2=GA2+GC2+3GO2
View Solutionयदि A=[logx−1−logx2] और यदि det (A)=2, तब x का मान है
View SolutionΔABC का क्षेत्रफल c2−(b−a)2हैतब"tan"C/2 का मान है
View Solutionयदि बिन्दु (4, 2) का रेखा L = 0 के सापेक्ष प्रतिबिम्ब (-2, 6) है, तो L का समीकरण है
View Solution