दीर्घवृत x2a2+y2b2=1 के अन्तर्गत उस समद्विबाहु त्रिभुज का महत्तम क्षेत्रफल ज्ञात कीजिए जिसका शीर्ष दीर्घ अक्ष का एक सिरा है।
माना दीर्घवृत x2a2+y2b2=1 पर कोई बिन्दु P(acosθ,bsinθ) है।
P से PM⊥OX खीचिए और इसे आगे बढ़ाकर दीर्घवृत से Q पर मिलाए, तब ΔAPQ एक समद्विबाहु त्रिभुज है, माना इसका क्षेत्रफल S है, तब
S=2×12×AM×MP
=(OA−OM)×MP
=(a−acosθ)bsinθ
⇒S=ab(sinθ−sinθcosθ)
=ab(sinθ−12sin2θ)
⇒dSdθ=ab(cosθ−cos2θ)
पुनः θके सापेक्ष अवकलन करने पर,
d2Sdθ2=ab(−sinθ+2sin2θ)
उच्चतम और निम्नतम मान के लिए dSdθ=0
⇒cosθ=cos2θ⇒2θ=2π−θ⇒θ=2π3
θ=2π3पर,
(d2Sdθ2)θ=2π3=ab[−sin2π3+2sin(2×2π3)
=ab(−√32−2√32)=ab(−3√32)
=−3√3ab2<0
∴=2π3 पर S उच्चतम मान
=ab(sin(2π)3−12⋅2sin2π3cos2π3)
=ab(√32+√32×12)
=ab(2√3+√34)=3√34ab वर्ग मात्रक
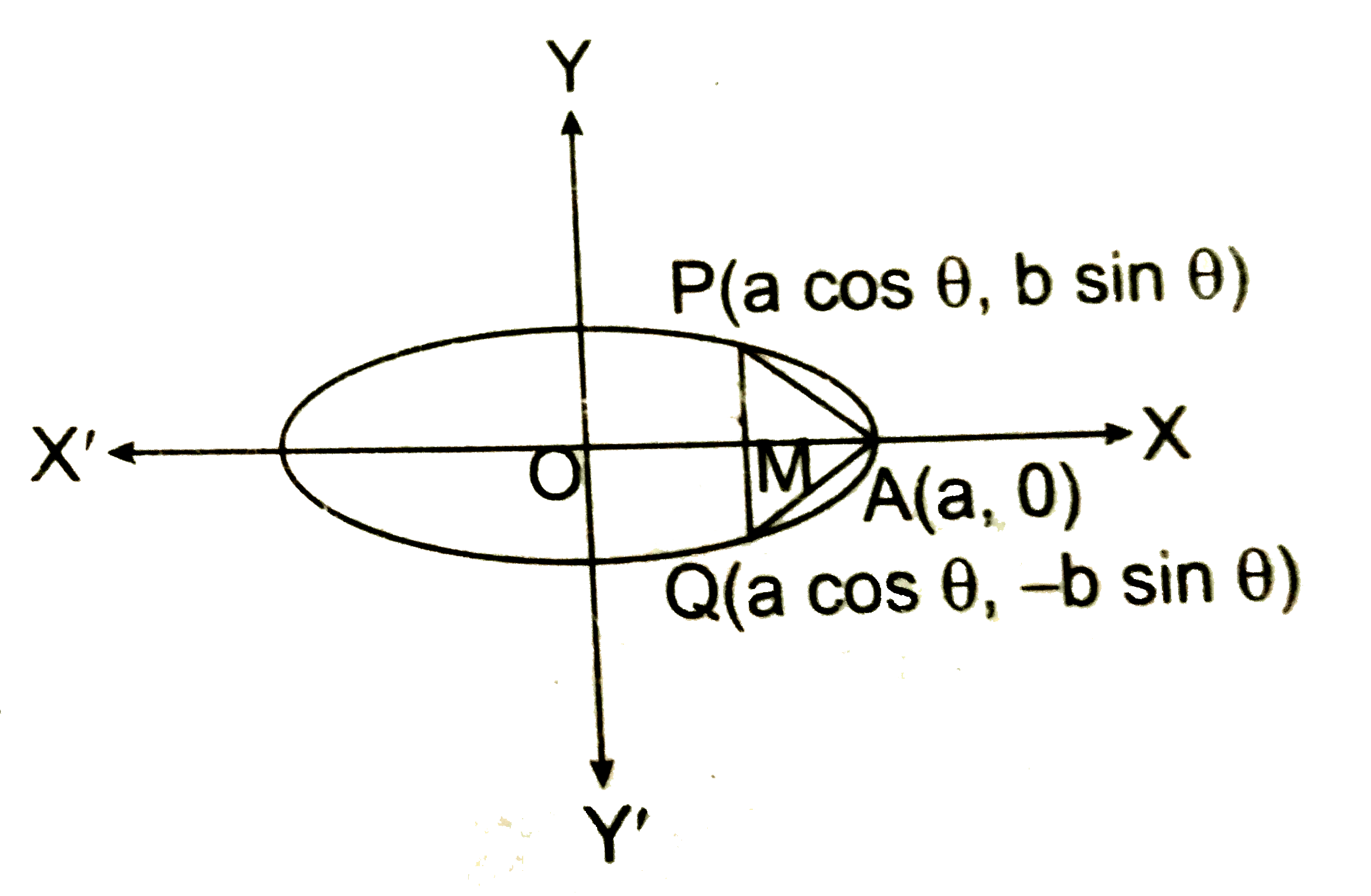
Topper's Solved these Questions
- अवकलन के अनुप्रयोग BOOK - NOOTAN HINDICHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6A
20 Videos
- अवकलन के अनुप्रयोग BOOK - NOOTAN HINDICHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6B
15 Videos
- अवकलन के अनुप्रयोग BOOK - NOOTAN HINDICHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6.5
48 Videos
- अवकल समीकरण BOOK - NOOTAN HINDICHAPTER - अवकल समीकरण EXERCISE - विविध प्रश्नावली
18 Videos
- आव्यूह BOOK - NOOTAN HINDICHAPTER - आव्यूह EXERCISE - विविध प्रश्नावली
15 Videos
Similar Questions
व्रत के क्षेत्रफल की परिवर्तन की दर, इसकी त्रिज्या r की सापेक्ष ज्ञात कीजिए जबकि r=3.5 सेमी है.
View Solutionसिद्ध कीजिए की फलन f(x)=3x+2,R पर एक निरन्तर वृद्धिमान फलन है.
View Solutionदिए गए फलानो के उच्चतम या निम्नतम मान, यदि कोई हो तो, ज्ञात कीजिए:
(i) f(x)=(2x−1)2+3
View Solutionनिम्नलिखित अवकल समीकरणों में से प्रत्येक की कोटि एवं घात (यदि परिभाषित हो) ज्ञात कीजिए।
(i) d2ydx2+5x(dydx)2−6y=logx
(ii) (dydx)3−4(dydx)2+7y=sinx
(iii) d4ydx4−sin(d3ydx3)=0
View Solutionमान लीजिए कि A=[0101] हो तो दिखाइए कि सभी n∈N के लिए (al+bA)n=anI+nan−1bA, जहाँ I कोटि 2 का तत्समक आव्यूह है ।
View Solutionवक्र y=logx,x−अक्ष,x=1/2तथाx=3/2 से घिरे भाग का क्षेत्रफल ज्ञात कीजिए।
View Solutionसिद्ध कीजिए कि समीकरण y2+2ax+2by+c=0 एक परवलय निरूपित करती है जिसका अक्ष x-अक्ष के समान्तर है । इसका शीर्ष ज्ञात कीजिए ।
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionउस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसकी भुजाओ के समीकरणy=ax,y=bx तथा ax+by+c=0 है
View Solutionउस दीर्घवृत का समीकरण ज्ञात कीजिए जो बिन्दुओ (−3,1) और (2,−2) से होकर जाता है तथा जिसका केंद्र मूलबिंदु पर है । उत्केंद्रता भी ज्ञात कीजिए ।
View Solutionपरवलय y=4−x2 तथा x -अक्ष से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए ।
View Solutionसदिशों के प्रयोग द्वारा उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष A(2,3,5),B(3,5,8) और C(2,7,8) हैं |
View Solutionउस त्रिभुज का अतः केंद्र ज्ञात कीजिए जिसके शीर्षों के निर्देशांक (1,2),(2,3) और (3,1) है ।
View Solutionउस बिंदु का बिन्दुपथ ज्ञात कीजिए
जिसका भुज सदैव 2 रहता है ।
View Solutionपरवलय y=x2−2x+3 का शीर्ष, नाभि, अक्ष तथा नियता का समीकरण ज्ञात कीजिए।
View Solutionसिद्ध कीजिए कि y2+2ax+2by+c=0 एक परवलय को निरूपित करता है जिसका अक्ष x-अक्ष के समांतर है। इसका शीर्ष तथा इसके नाभिलम्ब का समीकरण ज्ञात कीजिए।
View Solution
