सिद्ध कीजिए कि एक r त्रिज्या के गोले के अन्तर्गत उच्चतम आयतन के लम्ब वृत्तीय शंकु कि ऊँचाई 4r3है।
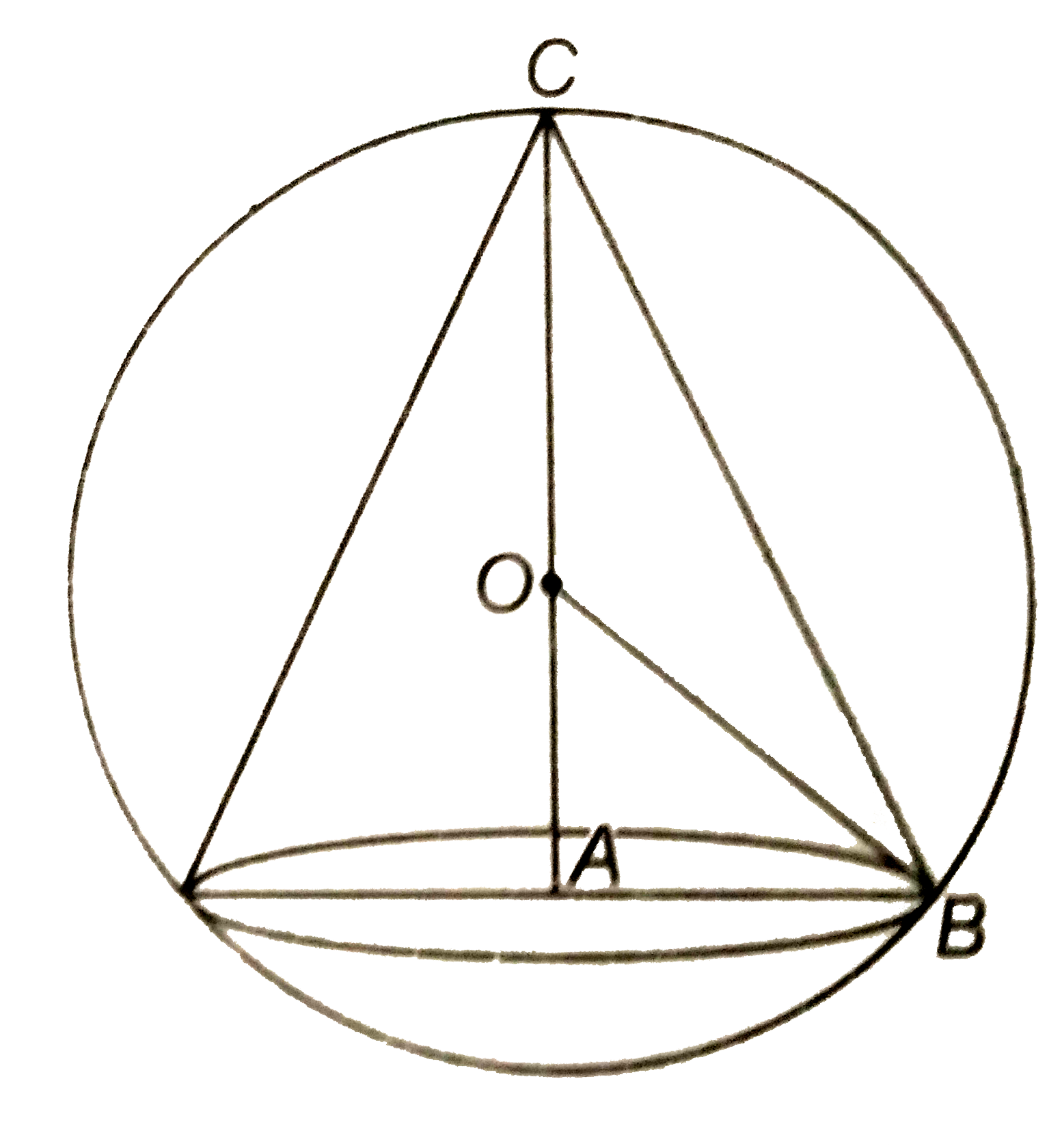
माना 'O ' केन्द्र और 'R ' त्रिज्या के गोले में आधार त्रिज्या 'r ' और ऊँचाई 'h ' का शंकु स्थति है। गोले का केन्द्र 'O ' शंकु की ऊँचाई AC पर होगा।
ΔOAB में,
OB2=OA2+AB2
R2=(h−R)2+r2
⇒0=h2−2hR+r2
⇒r2=2hR−h2 ।।।(1)
अब शंकु का आयतन
V=13πr2h
=13πh(2hR−h2) [समीकरण (1 ) से]
=13π(2h2R−h3)
dVdh=13π(4hR−3h2)
और d2Vdh=13π(4R−6h)
उच्चिष्ठ/निम्निष्ठ के लिये
dVdh=0
⇒hR−3h2=0
⇒4R=3h
⇒hR=43=4:3
h=4R3 पर
d2hdh2=13π(4R−8R)=−13π(4R)<0
⇒ आयतन महत्तम है।
अतः उच्चतम आयतन के लिये शंकु की ऊँचाई और गोले की त्रिज्या का अनुपात 4:3 होगा।
Topper's Solved these Questions
- अवकलन के अनुप्रयोग BOOK - NOOTAN HINDICHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6A
20 Videos
- अवकलन के अनुप्रयोग BOOK - NOOTAN HINDICHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6B
15 Videos
- अवकलन के अनुप्रयोग BOOK - NOOTAN HINDICHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6.5
48 Videos
- अवकल समीकरण BOOK - NOOTAN HINDICHAPTER - अवकल समीकरण EXERCISE - विविध प्रश्नावली
18 Videos
- आव्यूह BOOK - NOOTAN HINDICHAPTER - आव्यूह EXERCISE - विविध प्रश्नावली
15 Videos
Similar Questions
व्रत के क्षेत्रफल की परिवर्तन की दर, इसकी त्रिज्या r की सापेक्ष ज्ञात कीजिए जबकि r=3.5 सेमी है.
View Solutionसिद्ध कीजिए की फलन f(x)=3x+2,R पर एक निरन्तर वृद्धिमान फलन है.
View Solutionदिए गए फलानो के उच्चतम या निम्नतम मान, यदि कोई हो तो, ज्ञात कीजिए:
(i) f(x)=(2x−1)2+3
View Solutionनिम्नलिखित अवकल समीकरणों में से प्रत्येक की कोटि एवं घात (यदि परिभाषित हो) ज्ञात कीजिए।
(i) d2ydx2+5x(dydx)2−6y=logx
(ii) (dydx)3−4(dydx)2+7y=sinx
(iii) d4ydx4−sin(d3ydx3)=0
View Solutionमान लीजिए कि A=[0101] हो तो दिखाइए कि सभी n∈N के लिए (al+bA)n=anI+nan−1bA, जहाँ I कोटि 2 का तत्समक आव्यूह है ।
View Solutionसिद्ध कीजिए कि समीकरण y2+2ax+2by+c=0 एक परवलय निरूपित करती है जिसका अक्ष x-अक्ष के समान्तर है । इसका शीर्ष ज्ञात कीजिए ।
View Solutionसिद्ध कीजिए कि बिंदु (1,−6),(5,2),(7,0) तथा (−1,−4)एक चक्रीय चतर्भुज के शीर्ष है ।
View Solutionमाना कि N में एक द्वि - आधारी संकिया ∗, a∗b=a तथा b के LCM द्वारा परिभाषित है , a,b∈N तब सिद्ध कीजिए कि :(20∗16)∗8=20∗(16∗8)
View Solutionकथन सत्य है या असत्य
त्रिभुज कि भुजाओ के लम्ब समद्विभाजक संगामी होते है।
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionएक गोले कि त्रिज्या 7 सेमी. मापी जाती है जिसमे 0.02 सेमी. कि त्रुटि है। इस त्रुटि के कारण इसके आयतन कि गणना में सनिकटन त्रुटि ज्ञात कीजिए।
View Solutionवृत के क्षेत्रफल में परिवर्तन कि दर इसकी त्रिज्या r के सापेक्ष ज्ञात कीजिए जबकि r = 3 सेमी. तथा r = 4 सेमी. है
View Solutionएक गुब्बारा जो सदैव गोलाकार रहता है, का व्यास 32(2x+1) है इसके आयतन के परिवर्तन कि दर के सापेक्ष ज्ञात कीजिए।
View Solutionएक नली में 12 सेमी.3/से. कि दर से बालू उंडेली जा रही है। उंडेली गई बालू से एक शंकु का निर्माण इस प्रकार होता है कि शंकु कि ऊंचाई सदैव आधार कि त्रिज्या का 16 वा भाग होती ह। बालू के शंकु कि ऊंचाई में किस गति से वृद्धि हो रही है जबकि ऊंचाई 4 सेमी. है ?
View Solutionकिसी कारखाने में बने एक बल्ब कि 150 दिनों के उपयोग के बाद फ्यूज होने कि प्रायिकता 0 .05 है प्रायिकता ज्ञात कीजिए कि इस प्रकार के 5 बल्बों में से - एक से अधिक
View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
View Solution
