Question

उन बिन्दुओ को ज्ञात कीजिए जिन पर $f\left(x\right)={(x-2)}^4{(x+1)}^3$ द्वारा प्रदत्त फलन f का, (i ) स्थानीय बिन्दु है (ii ) स्थानीय निम्नतम बिन्दु है (iii ) नत परिवर्तन बिन्दु है।

Explanation

दिया गया समीकरण है, `f(x)=(x-2)^(4)(x+1)^(3)`
`f'(x)=(x-2)^(4)3(x+1)^(2)+(x+1)^(3)4(x-2)^(3)`
`=(x-2)^(3)(x+1)^(2){3(x-2)+4(x+1)}`
`=(x-2)^(3)(x+1)^(2)(7x-2)`
उच्चतम और निम्नतम मान के लिए `f'(x)=0`
`implies(x-2)^(3)(x+1)^(2)(7x-2)=0`
`impliesx=2,-1,2/7`
(i) `x=2/7` पर,

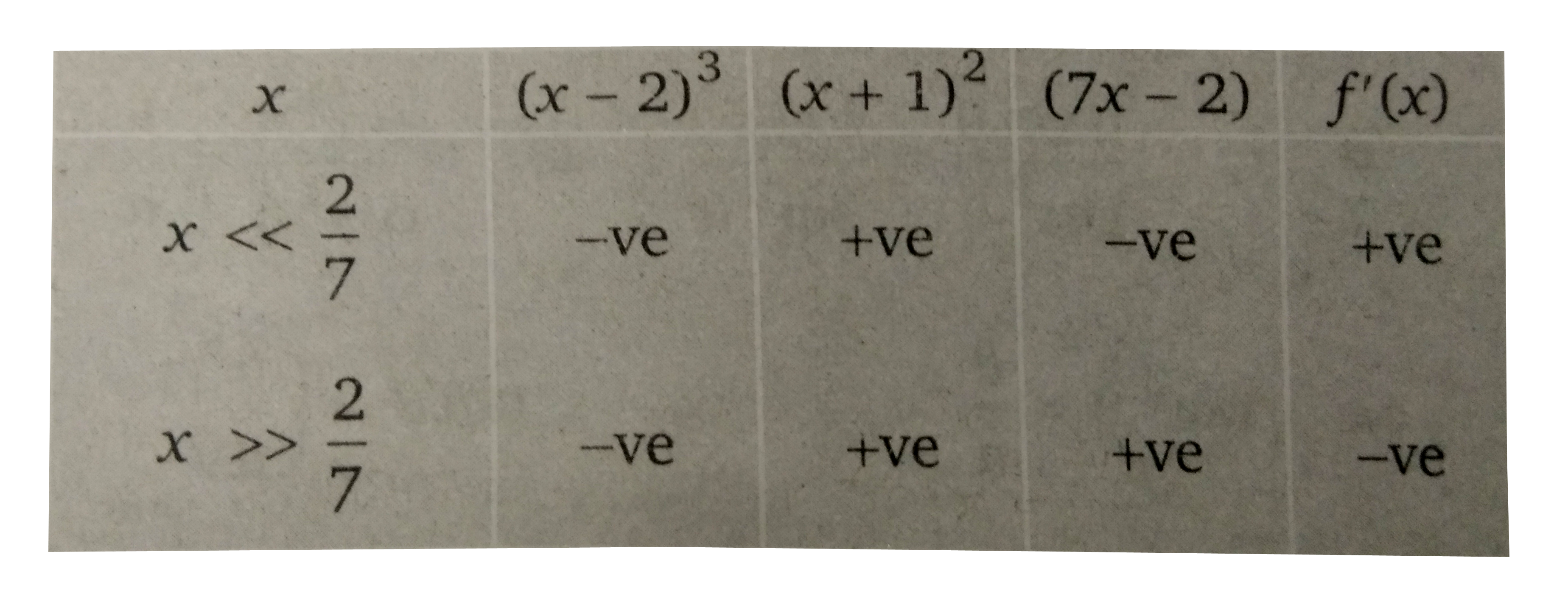
`thereforef'(क्ष)` अपना चिन्ह धनात्मक से तृणात्मक में बदलता है। इसलिए, `x=2//7` स्थानीय का बिन्दु है।
(ii ) `x = 2 ` पर,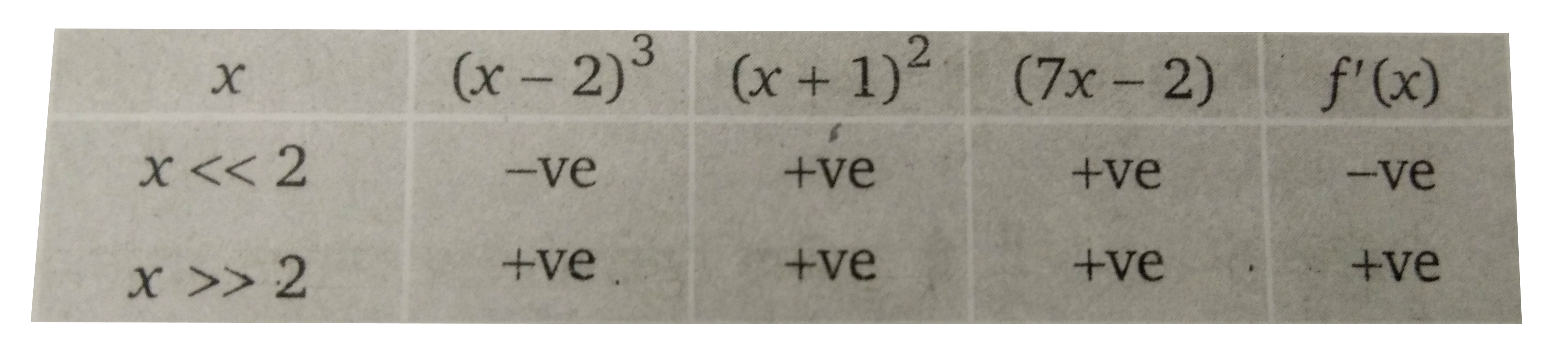
`thereforef'(x)` त्राणात्मक से घनात्मक चिन्ह बदलता है। अतः x = 2 स्थानीय निम्नतम होगा।
(iii) `x=-1` पर

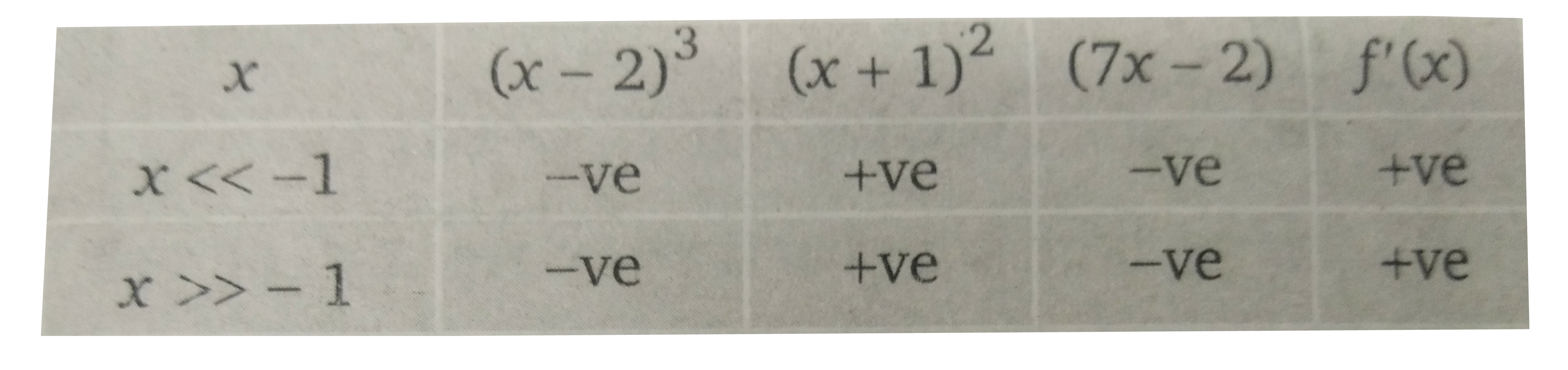
`thereforef'(x)` अपना चिन्ह नहीं बदलता है अतः x = 1 पर निति परिवर्तन होगा।