सिद्ध कीजिए कि अर्ध्द शीर्ष कोण α और ऊँचाई h के लम्ब वृत्तीय शंकु के अन्तर्गत अधिकतम आयतन के बेलन कि ऊँचाई, शंकु के ऊँचाई की एक तिहाई है और बेलन का अधिकतम आयतन 427πh3tan2α है।
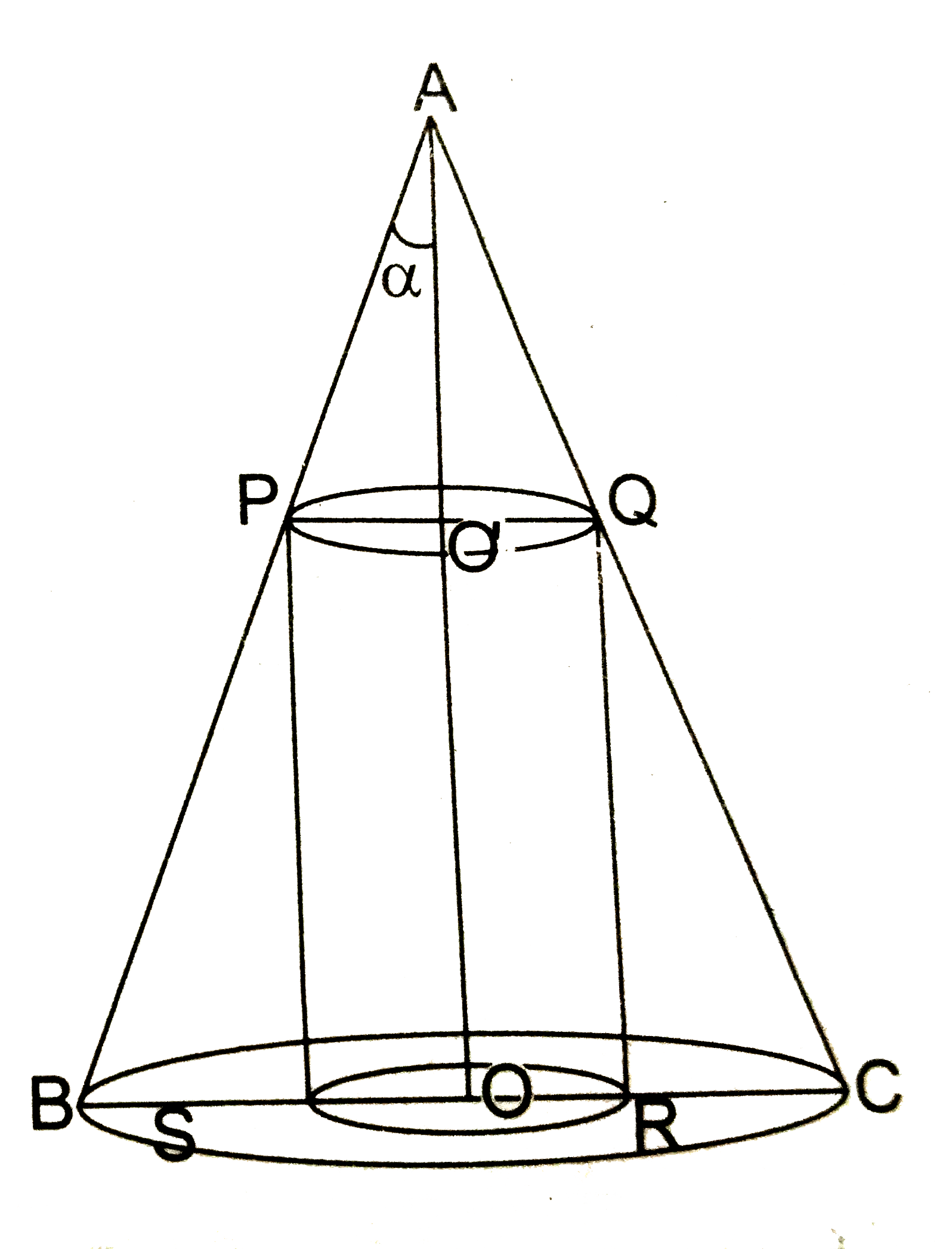
माना शंकु की ऊँचाई AO=hऔर ∠BAO=α
माना बेलन की त्रिज्या O 'P = x
ΔAPO' में, tanα=PO'AO'
⇒AO'=xcotα=h−xcotα
अब बेलन का आयतन
V=πx2⋅(OO')
=πx2(h−xcotα)
=π(hx2−x3cotα)
⇒dVdx=π(2h−3x2cotα)
और d2Vdx2=π(2h−6xcotα)
उच्चिष्ठ/निम्निष्ठ के लिये dVdx=0
⇒2hx=3x2cotα⇒x=2h3tanα
x=2h3tanα पर
d2Vdx2=π(2h−4h)=−2πh<0
⇒ आयतन V महत्तम है अब महत्तम आयतन
V=π{h(2h3tanα)2−(2h3tanα)3cotα}
=πh3tan2(49−827)=427πh3tan2α
Topper's Solved these Questions
- अवकलन के अनुप्रयोग BOOK - NOOTAN HINDICHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6A
20 Videos
- अवकलन के अनुप्रयोग BOOK - NOOTAN HINDICHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6B
15 Videos
- अवकलन के अनुप्रयोग BOOK - NOOTAN HINDICHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6.5
48 Videos
- अवकल समीकरण BOOK - NOOTAN HINDICHAPTER - अवकल समीकरण EXERCISE - विविध प्रश्नावली
18 Videos
- आव्यूह BOOK - NOOTAN HINDICHAPTER - आव्यूह EXERCISE - विविध प्रश्नावली
15 Videos
Similar Questions
व्रत के क्षेत्रफल की परिवर्तन की दर, इसकी त्रिज्या r की सापेक्ष ज्ञात कीजिए जबकि r=3.5 सेमी है.
View Solutionसिद्ध कीजिए की फलन f(x)=3x+2,R पर एक निरन्तर वृद्धिमान फलन है.
View Solutionदिए गए फलानो के उच्चतम या निम्नतम मान, यदि कोई हो तो, ज्ञात कीजिए:
(i) f(x)=(2x−1)2+3
View Solutionनिम्नलिखित अवकल समीकरणों में से प्रत्येक की कोटि एवं घात (यदि परिभाषित हो) ज्ञात कीजिए।
(i) d2ydx2+5x(dydx)2−6y=logx
(ii) (dydx)3−4(dydx)2+7y=sinx
(iii) d4ydx4−sin(d3ydx3)=0
View Solutionमान लीजिए कि A=[0101] हो तो दिखाइए कि सभी n∈N के लिए (al+bA)n=anI+nan−1bA, जहाँ I कोटि 2 का तत्समक आव्यूह है ।
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionत्रिज्या r तथा ऊँचाई h वाले बेलन के लिए त्रिज्या के सापेक्ष पृष्ठीय क्षेत्रफल में परिवर्तन की दर ज्ञात करो।
View Solutionएक चतुष्फलक के चारो शीर्ष O(0,0,0), A(1,2,1),B(2,1,3) और C(-1,1,2) है चतुफलक का आयतन ज्ञात कीजिए।
View Solutionकिसी बेलन का अर्धव्यास 2 मी/से की दर से बढ़ता है और ऊँचाई 3 मी/से की दर से घटती है। जब उसकी ऊँचाई 5 मी और अर्धव्यास 3 मी हो, तो बेलन के आयतन के परिवर्तन की दर होगी
View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
View Solutionलम्ब वृत्तीय बेलन का आयतन|उदाहरण
View Solutionबेलन का आयतन|उदाहरण#!#शंकु का आयतन
View Solutionपृष्ठीय क्षेत्रफल और आयतन|शंकु का आयतन#!#शंकु के आयतन पर आधारित महत्वपूर्ण प्रश्न
View Solutionपृष्ठीय क्षेत्रफल और आयतन|शंकु के पृष्ठीय क्षेत्रफल और आयतन पर आधारित प्रशन
View Solutionपृष्ठीय क्षेत्रफल और आयतन#!#शंकु का पृषठीय क्षेत्रफल#!#शंकु का आयतन#!#परीक्षा के लिए प्रश्न
View Solutionपृष्ठीय क्षेत्रफल और आयतन#!#शंकु का पृष्ठीय क्षेत्रफल#!#शंकु का आयतन#!#परीक्षा के लिए महत्वपूर्ण प्रश्न
View Solution
