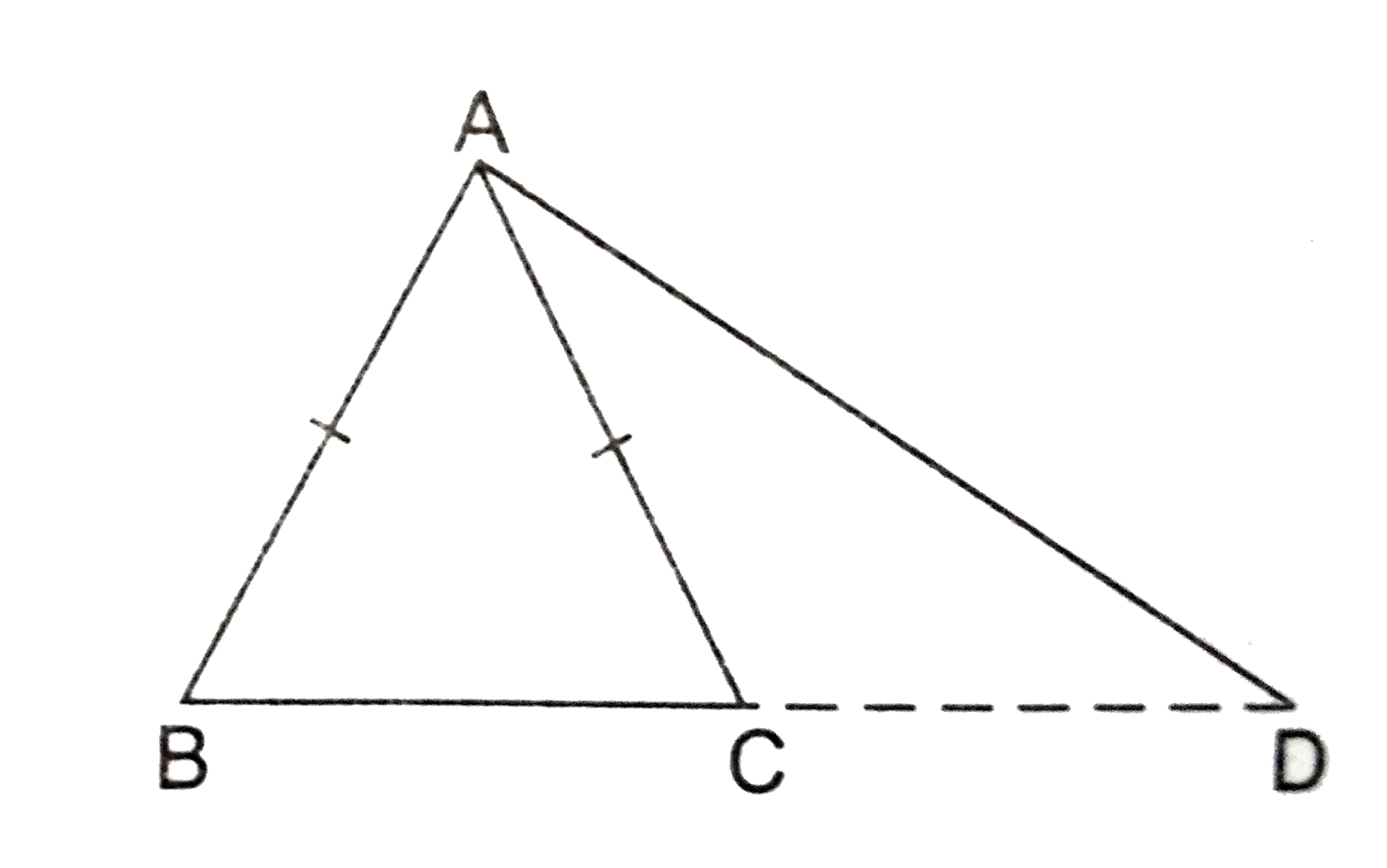
यदि एक समद्विबाहु त्रिभुज ABC में AB =AC तथा शीर्ष B से भुजा AC पर लम्ब BD हो तो सिद्ध करो की
समकोण त्रिभुज ADB में पाइथागोरस प्रमेय से

Topper's Solved these Questions
- त्रिभुजेंBOOK - RD SHARMACHAPTER - त्रिभुजेंEXERCISE - प्रश्नावली 4.1
12 Videos
- त्रिभुजेंBOOK - RD SHARMACHAPTER - त्रिभुजेंEXERCISE - प्रश्नावली 4.2
20 Videos
- त्रिकोणमितीय सर्वसमिकाएँ BOOK - RD SHARMACHAPTER - त्रिकोणमितीय सर्वसमिकाएँ EXERCISE - बहु विकल्पीय प्रश्न
28 Videos
- दो चार वाले रैखिक समीकरण युग्म BOOK - RD SHARMACHAPTER - दो चार वाले रैखिक समीकरण युग्म EXERCISE - बहु विकल्पीय प्रश्न
16 Videos
Similar Questions
कोष्ठक में दिए हुए शब्दों में से ही शब्दों को चुनकर रिक्त स्थान को भारिये:
सभी वृत.......(सर्वांगसम, समरूप) होते है|
View Solutionत्रिभुज ABC की भुजाओं AB और AC बिंदु D और E इस प्रकार है की DE भुजा BC के समानांतर है| यदि|||
AD=6 सेमि , DB = 9 सेमि तथा AE =8 सेमि, हो तो AC ज्ञात करो|
View Solutionयदि secθ+tanθ=x हो तो secθ=
View Solutionनिम्न समीकरण युग्म का अद्वितीय हल होंगे, यदि
kx−y=2
6x−2y=3
View SolutionIn quadrilatcal ABCD,prove that AB+BC+CD+AD<2(BD+AC)
View SolutionABC is a triangle in which AB=AC and D is a point on AC such that BC^(2)=AC xx CD .Prove that BD=BC .
View SolutionIn ABC , AD is perpendicular to BC . Prove that: AB2+CD2=AC2+BD2 (ii) AB2−BD2=AC2−CD2
View SolutionIn an isoscles ΔABC,AB=ACandD is a point on BC. Prove that AB2−AD2=BD⋅CD.
View SolutionIn ΔABC,AB=AC. Side BC is produced to D. Prove that (AD2−AC2)=BD⋅CD.
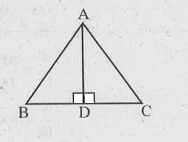
View Solutionएक △ABC में, यदि AD, BC के लंबवत है तो सिद्ध कीजिए कि
(i) AB2+CD2=AC2+BD2
(ii) AB2−BD2=AC2−CD2
View Solutionएक त्रिभुज ABC है | जिसमे AB = AC तथा D, BC पर कोई बिंदु है | तो सिद्ध कीजिए कि
AB2−AD2=BD⋅CD
View Solutionएक △ABC में, AB = AC तथा D, AC का मध्य बिंदु है और BC2=AC×CD हो तो सिद्ध कीजिए कि BD = BC
View Solutionसमद्विबाहु त्रिभुज ABC में AB=AC तथा BD⊥AC हो, तो सिद्ध कीजिए कि BD2−CD2=2CD.AD
View SolutionAB और CD का मध्य बिंदु O है | सिध्द करो कि (i)AOC≅BOD
(2)AC=BD तथा AC||BD.
View SolutionIn Δ ABC , AD ⊥BC and AD2=BD×CD. Prove that AB2+AC2= (BD+CD)2

View Solution△ABC ಯಲ್ಲಿ AD⊥BC ಮತ್ತು AD2=BDxCD ಆಗಿದೆ. ಹಾಗಾದರೆ AB2+AC2=(BD+CD)2 ಎಂದು ಸಾಧಿಸಿ.
View Solution
