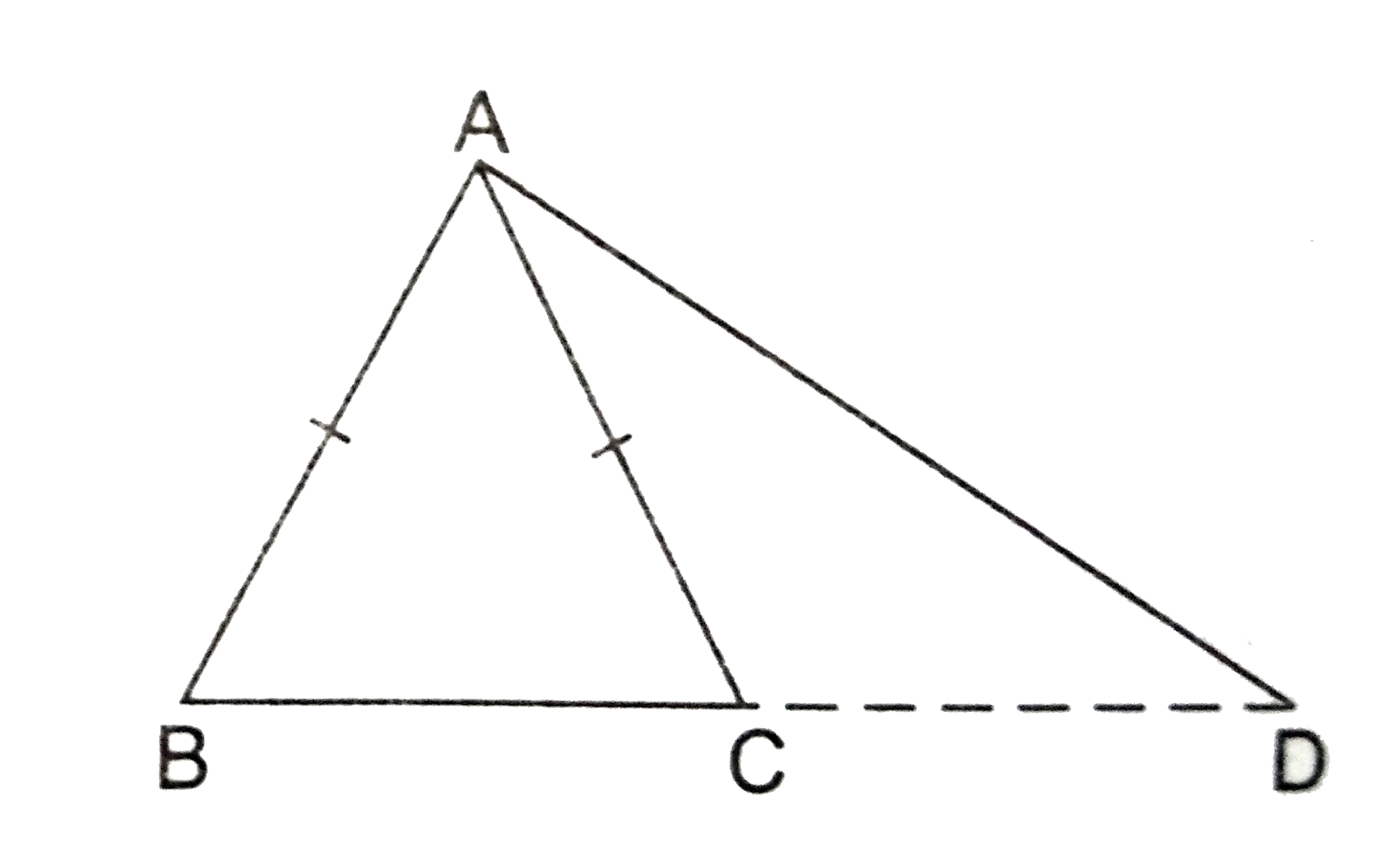
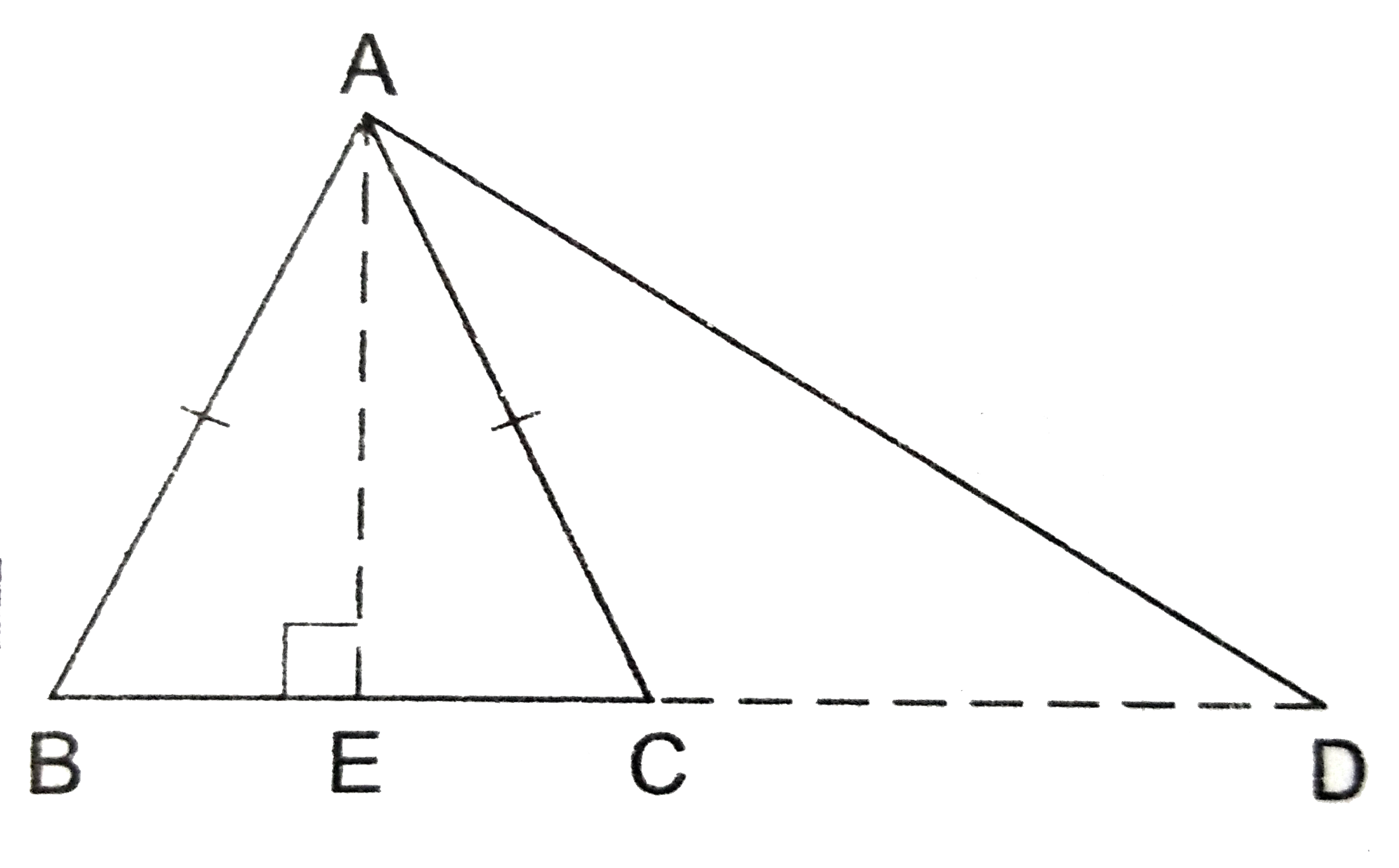
In ΔABC,AB=AC. Side BC is produced to D. Prove that (AD2−AC2)=BD⋅CD.
Video Solution
Text Solution
Draw AE⊥BC. Then BE=CE
AD2=AE2+DE2andAC2=AE2+CE2
⇒(AD2−AC2)=DE2−CE2
=(DE+CE(DE−CE)
=(DE+BE)(DE−CE)[∴CE=BE]
=BD⋅CD
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7E30videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Multiple Choice Questions (Mcq)53videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7C13videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 1127videos
T-RATIOS OF SOME PARTICULAR ANGLES
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself20videos
TRIGONOMETRIC IDENTITIES
Similar Questions
Knowledge Check
- Question 1 - Select One
ABC is an isosceles triangle with AB = AC. Side BA is produced to D such that AB=AD. Find the ∠BCD:
A100∘B60∘C80∘D90∘ - Question 2 - Select One
ΔABC,AB=AC and BA is produced to D such that AC = AD. Then the ∠BCD is
A100∘B60∘C80∘D90∘
abc is an isosceles triangle with AB=AC. Side BAis produced to D such that AB=AD. Prove that ∠BCD is a right angle.
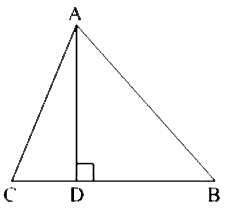
View SolutionIn ΔABC, seg AD⊥ seg BCDB=3CD.
Prove that : 2AB2=2AC2+BC2
 View Solution
View SolutionIn an isosceles triangle ABC with AB = AC, BD is perpendicular from B to side AC. Prove that BD2−CD2=2CD.AD
View SolutionABC is a triangle in which AB=AC and D is any point in BC . Prove that AB2−AD2=BDCD .
View SolutionIn △ABC,AB>AC and D is any point on BC. Prove that, AB > AD.
View SolutionIn ΔABC seg AD⊥segBC,DB=3CD Prove that 2AB2=2AC2+BC2
View Solution

