ABC is a triangle in which AB=ACandD is a point on AC such that BC2=AC×CD.Prove that BD=BC.
To prove that BD=BC given that BC2=AC×CD in triangle ABC where AB=AC and D is a point on AC, we can follow these steps:
1. Given Information:
- Triangle ABC with AB=AC.
- Point D on line segment AC.
- The relationship BC2=AC×CD.
2. Rearranging the Given Equation:
- From the equation BC2=AC×CD, we can rewrite it as:
BCCD=ACBC
- This can be derived by taking the square root of both sides:
BCCD=ACBC
3. Using Similar Triangles:
- Consider triangles ABC and BDC. Since AB=AC and they share angle C, by the Angle-Angle (AA) criterion, triangle ABC is similar to triangle BDC.
4. Setting Up Proportions:
- From the similarity of triangles, we have:
ABBD=BCDC
- Since AB=AC, we can replace AB with AC:
ACBD=BCDC
5. Cross Multiplying:
- Cross-multiplying gives us:
AC⋅DC=BC⋅BD
6. Using the Given Condition:
- From the earlier step, we already have BC2=AC⋅CD. We can replace AC⋅CD with BC⋅BD:
BC2=BC⋅BD
7. Dividing Both Sides by BC:
- Assuming BC≠0, we can divide both sides by BC:
BC=BD
Conclusion
Thus, we have proved that BD=BC.
- Triangle ABC with AB=AC.
- Point D on line segment AC.
- The relationship BC2=AC×CD.
- From the equation BC2=AC×CD, we can rewrite it as:
BCCD=ACBC
- This can be derived by taking the square root of both sides:
BCCD=ACBC
- Consider triangles ABC and BDC. Since AB=AC and they share angle C, by the Angle-Angle (AA) criterion, triangle ABC is similar to triangle BDC.
- From the similarity of triangles, we have:
ABBD=BCDC
- Since AB=AC, we can replace AB with AC:
ACBD=BCDC
- Cross-multiplying gives us:
AC⋅DC=BC⋅BD
- From the earlier step, we already have BC2=AC⋅CD. We can replace AC⋅CD with BC⋅BD:
BC2=BC⋅BD
- Assuming BC≠0, we can divide both sides by BC:
BC=BD
Thus, we have proved that BD=BC.
Topper's Solved these Questions
Similar Questions
ABC is a triangle in which AB = AC and D is any point on BC. Prove that:
AB2−AD2=BD.CD
View SolutionIn triangle ABC, D is a point in side AB such that AB = 4AD and E is a point in AC such that AC = 4AE. Show that BC : DE = 4:1
View SolutionIn triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View SolutionIn triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View SolutionIn ΔABC,AB=AC and D is a point in BC so that BD=CD. Prove that AD bisects ∠BAC.
View SolutionIn ΔABC,AB=ACandD is a point an side AC such that AD = BD = BC . Show that : ∠ADB=108∘
View SolutionThe given figure shows a triangle ABC, in which AB>AC. E is the mid-point of BC and AD is perpendicular to BC. Prove that AB2−AC2=2BC×ED.
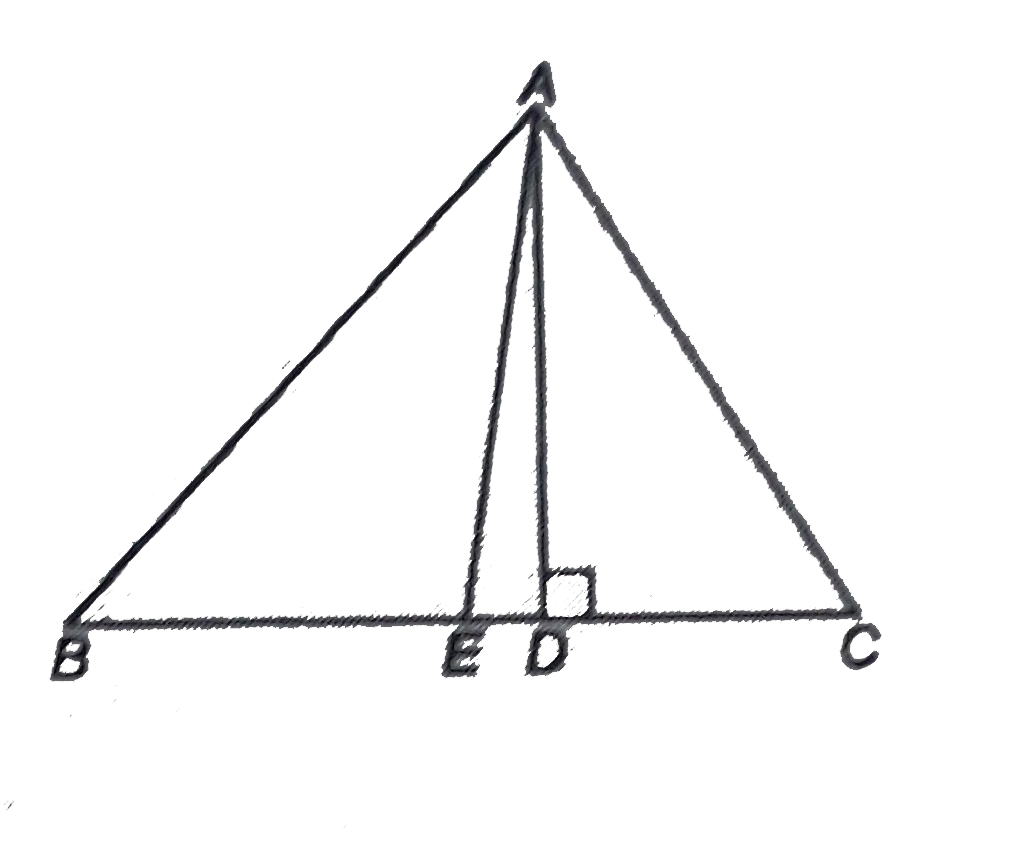
View SolutionABC is a right angled triangle with ABC=90∘. D is any point on AB and DE is perpendicular to AC. Prove that:

If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
View SolutionIn an isosceles triangle ABC, AB = AC and D is a point on BC produced. Prove that :
AD2=AC2+BD.CD
View SolutionD is any point on side AC of a ΔABC with AB= AC .Show that CD<BD.
View Solution
