सिद्ध कीजिए की किसी ट्रांजिस्टर के लिए धारा लाभों α व β के व्युत्क्रमों का अंतर् एक होता है| यदि β=50α, है, तो α का मान ज्ञात कीजिए|
धारा लाभ β तथा α में सम्बन्ध - β व α को प्रवर्धन गुणांक या धारा लाभ कहते है|
ट्रांजिस्टर के किसी भी विन्यास के लिए उत्सर्जक धारा IE सदैव आधार धारा IB तथा संग्रहक धारा IC के योग के बराबर होती है, अर्थात
ΔIE=ΔIC+ΔIB
ΔIEΔIC=ΔICΔIC+ΔIBΔIC..............(1)
परन्तु ΔICΔIE=α,∴ΔIEΔIC=1α
तथा ΔICΔIB=β,∴ΔIBΔIC=1β
समीकरण (1) में मान रखने पर
1α=1+1β
1α−1β=1
लेकिन दिया गया है −β=50α
मान रखने पर 1α−150α=1
4950α=1
α=4950=0.98
α=0.98
Topper's Solved these Questions
- इलेक्ट्रॉनिकी BOOK - SANJEEV PUBLICATIONCHAPTER - इलेक्ट्रॉनिकी EXERCISE - अन्य महत्वपूर्ण प्रशन (बोधात्मक प्रशन)
6 Videos
- इलेक्ट्रॉनिकी BOOK - SANJEEV PUBLICATIONCHAPTER - इलेक्ट्रॉनिकी EXERCISE - अन्य महत्वपूर्ण प्रशन (निबंधात्मक प्रशन)
10 Videos
- इलेक्ट्रॉनिकी BOOK - SANJEEV PUBLICATIONCHAPTER - इलेक्ट्रॉनिकी EXERCISE - पाठ्यपुस्तक के प्रशन (आंकिक प्रशन)
7 Videos
- किरण प्रकाशिकी BOOK - SANJEEV PUBLICATIONCHAPTER - किरण प्रकाशिकी EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (उच्च स्तरीय बुद्धि-कौशल प्रश्न )-
9 Videos
Similar Questions
C, Si तथा Ge की जालक (Lattice) संरचना समान होती है| फिर भी क्यों स विघुतरोधी है जबकि Si व Ge नैज अर्धचालक (intrinsic semiconductor) है?
View Solutionऊर्जा बैंड सिद्धांत पर चालकों, अर्धचालकों तथा कुचालकों में अंतर स्पष्ट कीजिये|
View Solutionकक्ष ताप पर शुद्ध जर्मेनियम की एक प्लेट जिसका क्षेत्रफल 2×10−4m2 तथा मोटाई 1.2×10−3m है में उत्पन्न विघुत धारा ज्ञात करो जब इसके फलको के मध्य 5V का विभवांतर आरोपित किया जाता है| कक्ष ताप पर जर्मेनियम में नैज आवेश वाहक धनत्व 1.6×106/m3 है| इलेक्ट्रान तथा हॉल की गतिशीलताएँ क्रमश: 0.4 m2V−1s−1 तथा 0.2m2V−1s−1 है|
View Solutionनिम्नलिखित प्रश्न ों के उत्तर लिखिए-
(a) निम्न चित्र में अपवर्तनांक 1.68 के तंतु से बानी किसी प्रकाश नलिका (लाइट पाइप) का अनुप्रस्थ परिछेद दर्शाया गया है| नलिका का बाह्म आवरण 1.44 अपवर्तनांक के पदार्थ का बना है| नलिका के अक्ष से आपतित किरणों के कोणों का परिसर, जिनके लिए चित्र में दर्शाए अनुसार नलिका के भीतर पूर्ण परावर्तन होते है, ज्ञात कीजिए|
(b) यदि पाइप पर बाह्म आवरण न हो तो क्या उत्तर होगा?

View Solutionयदि →a और →b असंरेख है ,तो x का मान ज्ञात कीजिए| जिसके लिए सदिश α=(2x+1)→a−→b और β=(x−2)→a+→b संरेख है
View Solutionआकृति के अनुसार यदि ∠BAC=80∘ हो तो ∠BCP का मान ज्ञात कीजिए।
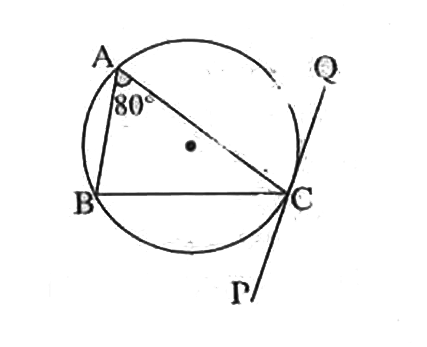
View Solutionसिद्ध कीजिए की किसी विषम पदों वाली समांतर श्रेढ़ी का योगफल श्रेढ़ी में माढ्य पद और पदों की संख्या के गुणगंफल के बराबर होता है |
View Solutionमाना की α,β समीकरण px2+qx+r=0,p≠0 के मूल है | यदि p,q,r समान्तर श्रेणी में हों तथा 1α+1β=4 तो | α−β | का मात्र है :
View Solutionमाना α तथा β समीकरण px2+qx+r=0,p≠0 के मूल हैं। यदि p,q, r समान्तर श्रेढ़ी में हैं तथा 1α+1β=4 है, तो |α−β | का मान है
View Solutionयदि समीकरण x2−2x+2=0 के मूल α तथा β हैं, तो n का न्यूनतम मान, जिसके लिए (αβ)n=1 है
View Solutionयदि z−αz+α(α∈R) एक शुद्ध रूप से काल्पनिक संख्या है तथा |z|=2 है तो α का एक मान है
View Solutionजहाँ ∣∣α2−β2∣∣=74 जहाँ α,β समीकरण 2x2+7x+c=0 के मूल हो, तो c का मान है।
View Solutionयदि tanα व् tanβ समीकरण x2−px+q=0 के मूल हो, तो sin2(α+β) का मान है
View Solutionयदि α,β,γ समीकरण x3−3x2+3x+7=0 के मूल है, एवम् w3=1: तो α−1β−1+β−1γ−1+γ−1α−1 का मान है।
View Solutionयदि α,βγ, समीकरण ax3+bx3+c=0 के मूल है | तो सारणिक ∣∣ ∣ ∣∣αββγγαβγγααβγααββγ∣∣ ∣ ∣∣ का मान होगा |
View Solutionयदि समीकरण ax2+bx+c=0 के मूल α व βहै तब αaβ+b+βaα+b बराबर है
View Solution
