काँच के पतले अवतालोत्तल लेंस (अपवर्तनांक 1.5 ) के उत्तल पृष्ठ की वक्रता त्रिज्या 20 सेमी है | अवतल पृष्ठ की वक्रता त्रिज्या 60 सेमी है | उत्तल पृष्ठ पर चाँदी की कलई की गई है तथा इसे क्षैतिज तल पर रखा जाता है |
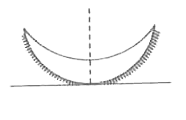
(a) मुख्य अक्ष पर एक पिन कहाँ रखी जाए, जिससे कि उसका प्रतिबिम्ब उसी स्थान पर बन जाए ?
(b) यदि अवतल भाग को जल ( अपवर्तनांक 4/3 ) से भर दिया जाए, तो बताइये पिन को कितना खिसकाना होगा कि पिन का प्रतिबिम्ब फिर पिन पर बने ?
The correct Answer is:(a) 15 सेमी (b) 1.15 सेमी
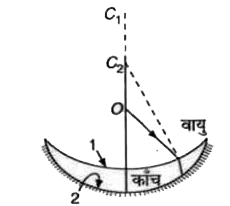
माना कि अवतल तथा उत्तल पृष्ठों के वक्रता - केंद्र क्रमशः C1 व C2 तथा वक्रता - त्रिज्यायें क्रमशः R1 व R2 हैं| पिन O तथा उसका प्रतिबिम्ब तब ही सम्पाती होंगें जब O से चलने वाली किरणें लेंस के अवतल पृष्ठ 1 पर अपवर्तित होकर कलई किये गए उत्तल पृष्ठ 2 पर अभिलंबवत गिरें | तब ये किरणें उसी मार्ग से वापिस लौटकर O पर ही प्रतिबिम्ब बनाएगी| चूँकि उत्तल पृष्ठ पर अभिलंबवत किरणें पीछे बढ़ाने पर उत्तल पृष्ठ के वक्रता केंद्र C2 पर मिलेगीं, अतः परावर्तन के लिए, v=R2 (उत्तल पृष्ठ की वक्रता त्रिज्या ) चूँकि यह अपवर्तन अवतल पृष्ठ 1 पर (जिसकी त्रिज्या R1 है) वायु से काँच में ही रहा है, अतः
μ2v−μ1u=μ2−μ1R1
यहाँ μ2=1.5,v=R2=−20 सेमी, R1=−60 सेमी
∴ 1.5−20−1−x=1.5−1−60
या x=15 सेमी
अतः पिन O को मुख्य अक्ष पर लेंस से 15 सेमी दूर रखेंगे |
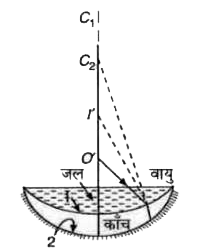
(b ) अवतल पृष्ठ को जल से भरने पर दो अपवर्तन होंगे, पहला वायु से जल में तथा दूसरा जल से काँच में| माना अब पिन O' पर है जिसकी लेंस से दुरी है| पुनः पिन व उसके प्रतिबिम्ब में सम्पात के लिए O' से चलने वाली किरणे दोनों अपवर्तनों के पश्चात परावर्तक उत्तल पृष्ठ 2 पर अभिलंबवत गिरनी चाहिएँ|
पहला अपवर्तन समतल पृष्ठ पर (R=∞) वायु से जल में हो रहा है| माना इसके द्वारा बना प्रतिबिम्ब I' है जिसकी दुरी v' है| अपवर्तन के लिए
μ2v'−1u'=μ2−1R=0 [∵R=∞]
अथवा μ2v'=1u'
∴ v'=(4/3)u'
जहाँ μ2=4/3
दूसरा अपवर्तन अवतल पृष्ठ पर (जिसकी त्रिज्या R1) है, जल से काँच में हो रहा है| इसके लिए I' वस्तु है तथा C2 प्रतिबिम्ब है|
सूत्रानुसार,
μ2v−1v'=n−1R1
अब μ2=.wμg=.aμg.aμw
=3/24/3=98
v=R2=−20 सेमी
v'=43u' तथा R1=−60 सेमी|
∴ 9/8−20−1(4/3)u'=(9/8)−1−60
हल कनरे पर u'=−13.85 सेमी|
अब पिन लेंस से 13.85 सेमी दूर होगा |
∴ पिन का विस्थापन =15−13.85=1.15 सेमी (लेंस की ओर)|
Topper's Solved these Questions
- प्रकाशिकीBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रकाशिकीEXERCISE - श्रृंखलाबद्ध - बोधन प्रकार
5 Videos
- प्रकाशिकीBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रकाशिकीEXERCISE - एकल पूर्णांक उत्तर प्रकार
7 Videos
- पदार्थ के गुणBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - पदार्थ के गुणEXERCISE - शृंखलाबद्ध-बोधन प्रकार (अनुच्छेद-IV)
2 Videos
- प्रयोगात्मक भौतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रयोगात्मक भौतिकी EXERCISE - बहुविकल्पीय प्रश्न II
3 Videos
Similar Questions
चित्र में XY एक पृष्ठ है जो दो पारदर्शी माध्यमों, माध्यम -1 तथा माध्यम -2 को अलग करता है | रेखाएँ ab तथा cd माध्यम -1 में चल रहीं तथा पृष्ठ XY पर आपतित होने वाली प्रकाश - तरंग के तरंग्रागों को निरूपित करती हैं | रेखाएँ ef तथा gh अपवर्तन के बाद माध्यम -2 में चल रही प्रकाश तरंग के तरंग्रागों को निरूपित करती हैं |
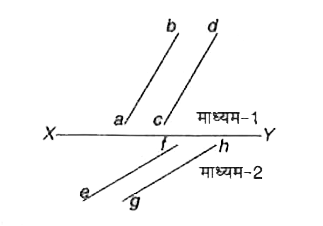
प्रकाश चल रहा ह
View Solutionएक पतले उभयोत्तल लेंस की फोकस दूरी 20 सेमी है | जब लेंस के सामने बिम्ब को 25 सेमी से 50 सेमी दूर ले जाया जाता है तो इसके प्रतिबिम्ब का आवर्धन m25 से n50 हो जाता है | m25m50 अनुपात का मान क्या होगा ?
View Solutionचित्र में दिखाई गयी पिचकारी में एक पिस्टन वायु को एक चंचू द्वारा बाहर धकेलता है। चंचू के सामने एकसमान अनुप्रस्थ-काट वाली पतली नली लगी है। नली का दूसरा सिरा द्रव से भरे एक छोटे पात्र में है। जब पिस्टन वायु को चंचू से बाहर धकेलता है, तब पात्र में द्रव उठकर चंचू में आ जाता है। ओर फुहार के रूप में बाहर निकलता है। चित्र में दिखाई गयी पिचकारी में पिस्टन तथा चंचू की त्रिज्याएँ क्रमशः 20 मिमी तथा मिमी है। पात्र का ऊपरी भाग वातावरण में खुला है।

पिस्टन को 5 मिमी/से की गति से धकेलने पर चंचू से बाहर वाली वायु की गति है
View Solutionएक छात्र ने u-v विधि से अवतल दर्पण की फोकस दूरी निकालने का प्रयोग किया। प्रयोग में उपयोग किये गये अवतल दर्पण की फोकस दूरी 24 cm तथा प्रकाशीय बैच की लम्बाई 1.5 m थी। प्रतिबिम्ब की स्थिति के निर्धारण में हुई अधिकतम त्रुटि 0.2 cm हो सकती है। छात्र द्वारा लिखे गये (u.v) के पांच मान (cm में) इस प्रकार थे. (42.56). (48.48). (60, 40). (66.33). (78.39)। (u.v) के मान जो प्रयोग के द्वारा प्राप्त नही हो सकते और गलत लिखे गये, वह है (वे हैं)
View Solutionकिसी बिंदु आवेश के कारण उस बिंदु को केंद्र मानकर खींचे गए 10cm त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स −1.0×103Nm2/C त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स। (a) यदि गॉऊसीय पृष्ठ की त्रिज्या दो गुनी कर दी जाए तो पृष्ठ से कितना फ्लक्स गुजरेंगा ? (b) बिंदु आवेश का मान क्या है।
View Solutionएक बिंदु वस्तु एक काँच जिसका अपवर्तनांक (μs=32) है, से बने 20 सेमी फोकस दूरी वाले उत्तल लेन्स से 30 सेमी की दूरी पर रखी है। वस्तु का अन्तिम प्रतिबिमब अनन्त पर बनेगा यदि
View Solutionएक परवलय की नाभि मूलबिंदु पर है तथा रेखा x=2 परवलय की नियता है , तो परवलय का शीर्ष है
View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है, की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है ,की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
View Solutionयदि वृत्त के केंद्र से 3 सेमी. की दूरी पर स्थित जीवा की लम्बाई 8 सेमी. है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionबिहारी ने ग्रीष्म ऋतु की तुलना किससे की है ? प्राणियों पर उसका क्या प्रभाव पड़ता है ?
View Solutionजब 'r त्रिज्या का एक हवा का बुलबुला किसी झील की तली से सतह तक उठता है तो उसकी त्रिज्या 5r/4 हो जाती है (वायुमण्डलीय दाब जल स्तम्भ की 10 मीटर की ऊंचाई के बराबर है)। यदि ताप नियत है तथा पृष्ठ तनाव को उपेक्षणीय माना गया है, तो झील की गहराई है
View Solution
