संलग्न चित्र में n1 व n2(n2>n1) अपवर्तनांक के दो माध्यमों के समतल सीमा - पृष्ठ AB पर एकवर्णी प्रकाश आपतन कोण θ पर आपतित होता है | कोण दोनों माध्यमों के लिए क्रांतिक कोण से थोड़ा बड़ा है जिससे पूर्ण आतंरिक परावर्तन होता है | AB यदि एकसमान मोटाई की तथा अपवर्तनांक की एक पारदर्शी पट्टिका DEFG सीमा पृष्ठ पर चित्र की भाँति रख दी जाए, तो सिद्ध कीजिए कि n3 के किसी भी मान के लिए समस्त प्रकाश माध्यम II में अंततः वापिस परावर्तित हो जाएगा | स्थितियों (a) n3<n1 तथा (b) n3>n1 को अलग - अलग लें |
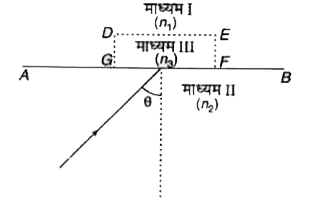
प्रश्नानुसार, θ का मान sin−1(n1n2) से थोड़ा अधिक है|
(a ) जब n3<n1
अर्थात n3<n1<n2
या n2n2<n1n2 या sin−1(n3n2)<sin−1(n1n2)
अतः III तथा II के लिए क्रांतिक कोण का मान II तथा I के लिए क्रांतिक कोण के मान से कम होगा | अब यदि पूर्ण आंतरिक परावर्तन की क्रिया I तथा II के बीच होती है तो I तथा III के बीच भी पूर्ण आंतरिक परावर्तन निश्चित रूप से होगा |
(b ) जब n3>n1
दो स्थितियों सम्भब हैं|
स्थिति I : n1<n3<n2
इस स्थिति में II तथा III के बीच पूर्ण आंतरिक परावर्तन (TIR ) नहीं होगा परन्तु III तथा I के बीच यह सम्भव होगा क्योंकि पहले प्रकाश किरण II से III में प्रवेश करती है अर्थात सघन से विरल माध्यम में|
∴ i>θ
P पर स्नैल के नियम से, n2sinθ=n3sini
या sini=(n2n3)sinθ
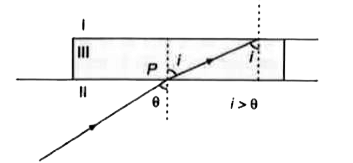
चूँकि sinθ का मान n1n2 से थोड़ा - सा अधिक है इसलिए sini का मान n2n3×n1n2 अर्थात n1n3 से थोड़ा अधिक होगा |
परन्तु n1n3=sin(θC)I, III
अतः sin(i),sin(θC)I, III से थोड़ा अधिक होगा तथा पूर्ण आंतरिक परावर्तन के फलस्वरूप प्रकाश किरण वापस आ जाएगी |
स्थिति II : n1<n2<n3
माध्यम II से III में जाते समय प्रकाश किरण अभिलम्ब की ओर मुद जाएग| स्नैल के नियम से
n2sinθ=n3sini⇒sini=n2n3sinθ
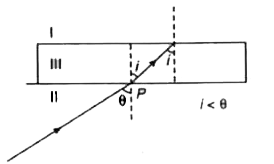
चूँकि sinθ,n1n2 से थोड़ा अधिक है अतः
sini का मान n2n3×n1n2 अर्थात n1n3 से कुछ अधिक ही होगा,
परन्तु n1nj3=sin(θ+C)I, III
अर्थात sini>sinθ(θC)I, III
∴ i>(θC)I, III
अतः पूर्ण आंतरिक परावर्तन सम्भव होगा तथा प्रकाश किरण वापस लौट आएगी |
Topper's Solved these Questions
- प्रकाशिकीBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रकाशिकीEXERCISE - श्रृंखलाबद्ध - बोधन प्रकार
5 Videos
- प्रकाशिकीBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रकाशिकीEXERCISE - एकल पूर्णांक उत्तर प्रकार
7 Videos
- पदार्थ के गुणBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - पदार्थ के गुणEXERCISE - शृंखलाबद्ध-बोधन प्रकार (अनुच्छेद-IV)
2 Videos
- प्रयोगात्मक भौतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रयोगात्मक भौतिकी EXERCISE - बहुविकल्पीय प्रश्न II
3 Videos
Similar Questions
चित्र में XY एक पृष्ठ है जो दो पारदर्शी माध्यमों, माध्यम -1 तथा माध्यम -2 को अलग करता है | रेखाएँ ab तथा cd माध्यम -1 में चल रहीं तथा पृष्ठ XY पर आपतित होने वाली प्रकाश - तरंग के तरंग्रागों को निरूपित करती हैं | रेखाएँ ef तथा gh अपवर्तन के बाद माध्यम -2 में चल रही प्रकाश तरंग के तरंग्रागों को निरूपित करती हैं |
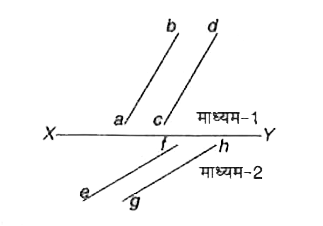
प्रकाश चल रहा ह
View Solutionएक पतले उभयोत्तल लेंस की फोकस दूरी 20 सेमी है | जब लेंस के सामने बिम्ब को 25 सेमी से 50 सेमी दूर ले जाया जाता है तो इसके प्रतिबिम्ब का आवर्धन m25 से n50 हो जाता है | m25m50 अनुपात का मान क्या होगा ?
View Solutionचित्र में दिखाई गयी पिचकारी में एक पिस्टन वायु को एक चंचू द्वारा बाहर धकेलता है। चंचू के सामने एकसमान अनुप्रस्थ-काट वाली पतली नली लगी है। नली का दूसरा सिरा द्रव से भरे एक छोटे पात्र में है। जब पिस्टन वायु को चंचू से बाहर धकेलता है, तब पात्र में द्रव उठकर चंचू में आ जाता है। ओर फुहार के रूप में बाहर निकलता है। चित्र में दिखाई गयी पिचकारी में पिस्टन तथा चंचू की त्रिज्याएँ क्रमशः 20 मिमी तथा मिमी है। पात्र का ऊपरी भाग वातावरण में खुला है।

पिस्टन को 5 मिमी/से की गति से धकेलने पर चंचू से बाहर वाली वायु की गति है
View Solutionएक छात्र ने u-v विधि से अवतल दर्पण की फोकस दूरी निकालने का प्रयोग किया। प्रयोग में उपयोग किये गये अवतल दर्पण की फोकस दूरी 24 cm तथा प्रकाशीय बैच की लम्बाई 1.5 m थी। प्रतिबिम्ब की स्थिति के निर्धारण में हुई अधिकतम त्रुटि 0.2 cm हो सकती है। छात्र द्वारा लिखे गये (u.v) के पांच मान (cm में) इस प्रकार थे. (42.56). (48.48). (60, 40). (66.33). (78.39)। (u.v) के मान जो प्रयोग के द्वारा प्राप्त नही हो सकते और गलत लिखे गये, वह है (वे हैं)
View Solutionk के किस मान के लिए रेखाएँ y=(2+√3)x+4 तथा y=kx+6 एक दूसरे से 60∘ के कोण पर झुकी है ?
View Solutionएकवर्णी प्रकाश का एक पुंज (beam of light) काँच की एक प्लेट पर 58^(@ के कोण पर आपतित होता है और परावर्तित किरणपुंज पूरी तरह समतल-ध्रुवित पाया जाता है। काँच का अपवर्तनांक निकालें।
View Solutionकिसी वृत्त की जीवा AB द्वारा केंद्र पर अंतरित कोण 140∘ है तो A तथा B बिन्दुओ पर खींची गयी स्पर्श रेखाओ के बीच का कोण ज्ञात कीजिए।
View Solutionकिसी वृत्त की जीवा AB द्वारा केंद्र पर अंतरित कोण 140∘ है तो A तथा B बिन्दुओ पर खींची गयी स्पर्श रेखाओ के बीच का कोण ज्ञात कीजिए।
View Solutionयदि वक्रों y=10−x2 तथा y=2+x2 के बीच एक प्रतिच्छेदन बिन्दु पर न्यून कोण θ है , तो |tanθ| बराबर है
View Solutionपरवलय x2=8y पर एक स्पर्श रेखा,जो X-अक्ष की धनात्मक दिशा के साथ कोण θ बनती है, का सभीकरण है
View Solutionएक वृत्त के अंतर्गत बने समबहुभुज की प्रत्येक भुजा केंद्र पर 45∘ का कोण बनाती है| बहुभुज का नाम दीजिए |
View Solutionक्रांतिक कोण|पूर्ण आंतरिक परावर्तन#!#पूर्ण आंतरिक परावर्तन के उपयोग
View Solutionदो समतलीय का सह-तलीय होना|दो समतलों के बीच कोण#!#समतल से दिए गए बिंदु की दूरी#!#एक रेखा एवं एक समतल के बीच कोण#!#उदाहरण
View Solutionप्रकाश का अपवर्तन|विभिन्न माध्यमों का अपवर्तनांक#!#क्रांतिक कोण तथा पूर्ण आंतरिक परावर्तन
View Solutionएक पुस्तक की मोटाई 2 सेमी है और इसमें 800 पृष्ठ है। एक पृष्ठ की मोटाई मानक रूप में ज्ञात कीजिए।
View Solution6328 Å तरंगदैर्ध्य का एक प्रकाश लम्बवत रूप से 0.2 mm चौड़ाई की झिरी पर आपतित होता है। परदे पर केंद्रीय उच्चिष्ठ की कोणीय चौड़ाई होगी
View Solution
