वायु में चलती हुई एक प्रकाश - किरण एक पारदर्शी माध्यम की लम्बी आयताकार पट्टिका पर जिसकी मोटाई t=1.0 मी है, पृष्ठसर्पी कोण ( आपतन कोण =90∘ ) पर आपतित है | आपतन बिंदु मूल बिंदु A(0,0) है | माध्यम का चर अपवर्तनांक n(y) है |
n(y)=[ky3/2+1]1/2
जहाँ k=1.0(मी)−3/2 तथा वायु का अपवर्तनांक 1.0 है |
![वायु में चलती हुई एक प्रकाश - किरण एक पारदर्शी माध्यम की लम्बी आयताकार पट्टिका पर जिसकी मोटाई t = 1.0 मी है, पृष्ठसर्पी कोण ( आपतन कोण = 90^(@) ) पर आपतित है | आपतन बिंदु मूल बिंदु A(0, 0) है | माध्यम का चर अपवर्तनांक n(y) है | n(y)=[ky^(3//2)+1]^(1//2) जहाँ k=1.0](https://d10lpgp6xz60nq.cloudfront.net/physics_images/ARH_HIN_41Y_JEE_PHY_SP_C12_E08_015_Q01.png)
(a) माध्यम में बिंदु B(x,y) पर किरण - पथ की प्रवणता तथा उसी बिंदु पर आपतन कोण में सम्बन्ध ज्ञात कीजिए |
(b) माध्यम में किरण - पथ की समीकरण y(x) प्राप्त कीजिए |
(c) बिंदु P के निर्देशांक (x1,y1) ज्ञात कीजिए जहाँ कि किरण पट्टिका वायु परिसीमा के ऊपरी तल को काटती है |
(d) बिंदु P के परे किरण - पथ दर्शाइए |
The correct Answer is:ढाल =coti (b) 4y1/4=x (c ) (4,1)
(a) अपवर्तनांक y का फलन है। यह Y-अक्ष के अनुदिश परिवर्ती है अर्थात दोनों माध्यमों को अलग करने वाली सीमा X-रेखा अक्ष के समान्तर है अर्थात किसी भी बिन्दु पर Y-अभिलम्ब अक्ष के समान्तर है।
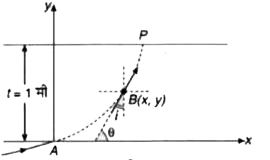
अपवर्तनांक , y के साथ बढ़ती है। इसलिए प्रकाश की किरण विरल से सघन माध्यम में जा रही है अर्थात यह अभिलम्ब की ओर झुक जायेगी। प्रकाश का पथ चित्रानुसार होगा।

चित्र (a) के अनुसार, पथ के किसी बिन्दु B पर माना आपतन कोण (i) है।
θ=90∘−i
या tanθ=tan(90∘−i)=coti
या ढाल=coti
(b) tanθ=dydx
∴ dydx=coti ....(i)
A तथा B पर स्नैल के नियम से,
nAsiniA=nBsiniB
nA=1 ∵ y=0
siniA=1 ∵iA=90∘
∴ nB=√ky3/2+1
=√y3/2+1 [∵k=1.0(मी)−3/2]
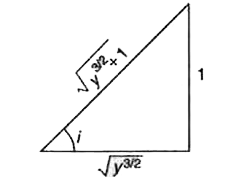
∴(1)(1)=√(y3/2+1)sini या sini=1√y3/2+1
∴ coti=√y3/2=y3/4 ...(ii)
सेमी (i) व (ii) से
dydx=y3/4 या y−3/4dy=dx
समाकलित करने पर पथ का समीकरण
4y1/4=x
(c) बिन्दु P पर, y=1.0 मी
∴ x=4.0 मी
इसलिए P के निर्देशांक
P≡(4,1)
(d) nAsiniA=npsinip(nA=np=1)
∴ ip=iA=90∘
अर्थात निर्गत किरण P पर सीमा रकेः के समान्तर होगी।
Topper's Solved these Questions
- प्रकाशिकीBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रकाशिकीEXERCISE - श्रृंखलाबद्ध - बोधन प्रकार
5 Videos
- प्रकाशिकीBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रकाशिकीEXERCISE - एकल पूर्णांक उत्तर प्रकार
7 Videos
- पदार्थ के गुणBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - पदार्थ के गुणEXERCISE - शृंखलाबद्ध-बोधन प्रकार (अनुच्छेद-IV)
2 Videos
- प्रयोगात्मक भौतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रयोगात्मक भौतिकी EXERCISE - बहुविकल्पीय प्रश्न II
3 Videos
Similar Questions
चित्र में XY एक पृष्ठ है जो दो पारदर्शी माध्यमों, माध्यम -1 तथा माध्यम -2 को अलग करता है | रेखाएँ ab तथा cd माध्यम -1 में चल रहीं तथा पृष्ठ XY पर आपतित होने वाली प्रकाश - तरंग के तरंग्रागों को निरूपित करती हैं | रेखाएँ ef तथा gh अपवर्तन के बाद माध्यम -2 में चल रही प्रकाश तरंग के तरंग्रागों को निरूपित करती हैं |
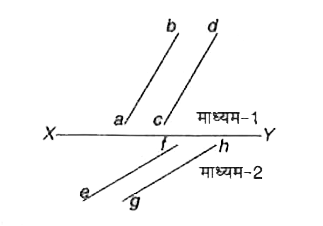
प्रकाश चल रहा ह
View Solutionएक पतले उभयोत्तल लेंस की फोकस दूरी 20 सेमी है | जब लेंस के सामने बिम्ब को 25 सेमी से 50 सेमी दूर ले जाया जाता है तो इसके प्रतिबिम्ब का आवर्धन m25 से n50 हो जाता है | m25m50 अनुपात का मान क्या होगा ?
View Solutionचित्र में दिखाई गयी पिचकारी में एक पिस्टन वायु को एक चंचू द्वारा बाहर धकेलता है। चंचू के सामने एकसमान अनुप्रस्थ-काट वाली पतली नली लगी है। नली का दूसरा सिरा द्रव से भरे एक छोटे पात्र में है। जब पिस्टन वायु को चंचू से बाहर धकेलता है, तब पात्र में द्रव उठकर चंचू में आ जाता है। ओर फुहार के रूप में बाहर निकलता है। चित्र में दिखाई गयी पिचकारी में पिस्टन तथा चंचू की त्रिज्याएँ क्रमशः 20 मिमी तथा मिमी है। पात्र का ऊपरी भाग वातावरण में खुला है।

पिस्टन को 5 मिमी/से की गति से धकेलने पर चंचू से बाहर वाली वायु की गति है
View Solutionएक छात्र ने u-v विधि से अवतल दर्पण की फोकस दूरी निकालने का प्रयोग किया। प्रयोग में उपयोग किये गये अवतल दर्पण की फोकस दूरी 24 cm तथा प्रकाशीय बैच की लम्बाई 1.5 m थी। प्रतिबिम्ब की स्थिति के निर्धारण में हुई अधिकतम त्रुटि 0.2 cm हो सकती है। छात्र द्वारा लिखे गये (u.v) के पांच मान (cm में) इस प्रकार थे. (42.56). (48.48). (60, 40). (66.33). (78.39)। (u.v) के मान जो प्रयोग के द्वारा प्राप्त नही हो सकते और गलत लिखे गये, वह है (वे हैं)
View Solutionपरवलय y2=4ax की नाभि तथा उस पर स्थित चर को मिलाने वाले रेखाखण्ड के मध्य - बिंदु का पथ एक परवलय है जिसकी नियता है :
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionदर्शाइए की बिंदु x=2at1+t2 तथा y=a(1−t2)1+t2 जहाँ a स्थिर राशि है t प्राचल है तथा −1≤t≤1,t के प्रत्येक मान के लिए वृत्त पर स्थित है ।
View Solutionएक परवलय की नाभि मूलबिंदु पर है तथा रेखा x=2 परवलय की नियता है , तो परवलय का शीर्ष है
View Solutionएकवर्णी प्रकाश का एक पुंज (beam of light) काँच की एक प्लेट पर 58^(@ के कोण पर आपतित होता है और परावर्तित किरणपुंज पूरी तरह समतल-ध्रुवित पाया जाता है। काँच का अपवर्तनांक निकालें।
View Solutionएक बिंदु P,2x−3y+4=0 पर गति करता है । यदि Q(1,4) तथा R(3,-2) निश्चित बिंदु है, तो ΔPQR के केन्द्रक का बिन्दुपथ (locus) एक रेखा है
View SolutionAB एक ऊर्ध्वाधर खंभा है, जिनका A सिरा जमीन पर है | C, AB का मध्य-बिंदु है और P जमीन पर एक बिंदु है | BC, बिंदु P पर β कोण बनता है | यदि AP = nAB हो, तो tanβ का मान है |
View SolutionA pole is standing on the top of a house. Height of house is 25 metres. The angle of elevation of the top of house from point P is 45^@ and the angle of elevation of the top of pole from P is 60^@ . Point P is on the ground level. What is the height (in meteres) of pole? एक घर की चोटी पर एक खम्भा खड़ा है। घर की ऊँचाई 25 मीटर है। बिंदु P से घर की चोटी का उन्नयन कोण 45^@ है तथा P से खम्भे की चोटी का उन्नयन कोण 60^@ है। बिंदु P भूमि कौ सतह पर है। खम्भे की ऊँचाई (मीटर में) क्या है?
View SolutionA flag of height 4 metres is standing on the top of a building. The angle of elevation of the top of the flag from a point X is 45^@ and the angle of elevation of the top of building from X is 30^@ .Point X is on the ground level. What is the height (in metres) of the building? एक झंडा जिसकी ऊँचाई 4 मीटर है, इस इमारत की चोटी पर खड़ा हुआ है। बिंदु X से झंडे की चोटी का उन्नयन कोण 45^@ है तथा X से इमारत की चोटी का उन्नयन कोण 30^@ है। बिंदु X जमीन की सतह पर है। इमारत की ऊँचाई (मीटर में) क्या है?
View Solutionसमाचार पत्र किस माध्यम का एक स्वरूप है ?
View Solutionमुद्रण-माध्यम का एक स्वरूप है
View Solutionसाहित्यिक अभिव्यक्ति में रचनात्मक लेखन का माध्यम है
View Solution
