mm तरंगदैर्ध्य की सूक्ष्मतरंगो का एक कलासम्बद्ध समान्तर पुंज यंग के द्विस्लिट उपकरण पर आपतित किया जाता है। स्लिटो के मध्य अन्तराल 1.0 mm है। सूक्ष्मतरंगो की तीव्रता पर्दे से 1.0 m दूरी पर स्लिटो के तल के समान्तर स्थित पर्दे पर मापी जाती है, जो कि चित्र में दर्शाया गया है।
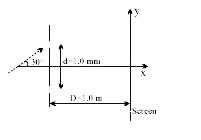
यदि आपतित पुंज द्वि-स्लिट उपकरण पर अधिलम्बवत् रूप से आपतित किया जाता है, तो पर्दे पर सभी व्यतरित निम्निष्ठ के y-निर्देशांक ज्ञात कीजिये।
The correct Answer is:(a) मी, मी (b) मी, 1.13 मी
मिमी , मिमी , मी
(a ) जब आपतन अभिलंवत हो, तब
तथा किरणों के मध्य पथांतर
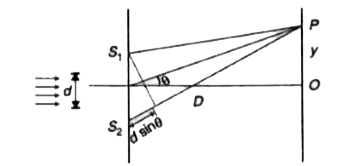
निम्नतम तीव्रता के लिए,
या
चूँकि
अतः n का मान 1 अथवा 2 हो सकता है|
जब
निम्निष्ठ की स्थिति,
मी
मी
चूँकि निम्निष्ठ O के किसी भी ओर हो सकता है, अतः मी तथा मी की दूरियों पर पर्दें पर चार निम्निष्ठ हो सकते हैं|
(b ) जब तथा तक पहुँचने से पूर्व किरणों में पथांतर
मिमी
अतः पथांतर दोनों किरणों में पहले से ही विघमान है|
केंद्रीय उच्चिष्ठ की स्थिति : केंद्रीय उच्चिष्ठ वह बिंदु है जहाँ कुल पथांतर शून्य होता है
अतः
या
या
या मी
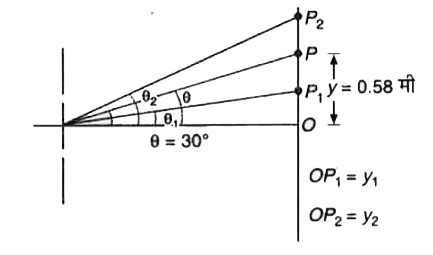
बिंदु P पर,
बिंदु P के ऊपर, तथा
बिंदु P के नीचे,
माना तथा केंद्रीय उच्चिष्ठ के दोनों ओर निम्निष्ठ हैं, तब के लिए
या
या
या
या मी मी
इसी प्रकार के लिए
या
या
या
या मी मी
अतः केंद्रीय उच्चिष्ठ के दोनों ओर प्रथम निम्निष्ठ के y - निर्देशांक, मी तथा मी|
Topper's Solved these Questions
- प्रकाशिकीBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रकाशिकीEXERCISE - श्रृंखलाबद्ध - बोधन प्रकार
5 Videos
- प्रकाशिकीBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रकाशिकीEXERCISE - एकल पूर्णांक उत्तर प्रकार
7 Videos
- पदार्थ के गुणBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - पदार्थ के गुणEXERCISE - शृंखलाबद्ध-बोधन प्रकार (अनुच्छेद-IV)
2 Videos
- प्रयोगात्मक भौतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रयोगात्मक भौतिकी EXERCISE - बहुविकल्पीय प्रश्न II
3 Videos
Similar Questions
चित्र में XY एक पृष्ठ है जो दो पारदर्शी माध्यमों, माध्यम -1 तथा माध्यम -2 को अलग करता है | रेखाएँ ab तथा cd माध्यम -1 में चल रहीं तथा पृष्ठ XY पर आपतित होने वाली प्रकाश - तरंग के तरंग्रागों को निरूपित करती हैं | रेखाएँ ef तथा gh अपवर्तन के बाद माध्यम -2 में चल रही प्रकाश तरंग के तरंग्रागों को निरूपित करती हैं |
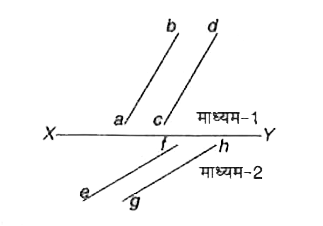
प्रकाश चल रहा ह
View Solutionएक पतले उभयोत्तल लेंस की फोकस दूरी 20 सेमी है | जब लेंस के सामने बिम्ब को 25 सेमी से 50 सेमी दूर ले जाया जाता है तो इसके प्रतिबिम्ब का आवर्धन m25 से n50 हो जाता है | m25m50 अनुपात का मान क्या होगा ?
View Solutionचित्र में दिखाई गयी पिचकारी में एक पिस्टन वायु को एक चंचू द्वारा बाहर धकेलता है। चंचू के सामने एकसमान अनुप्रस्थ-काट वाली पतली नली लगी है। नली का दूसरा सिरा द्रव से भरे एक छोटे पात्र में है। जब पिस्टन वायु को चंचू से बाहर धकेलता है, तब पात्र में द्रव उठकर चंचू में आ जाता है। ओर फुहार के रूप में बाहर निकलता है। चित्र में दिखाई गयी पिचकारी में पिस्टन तथा चंचू की त्रिज्याएँ क्रमशः 20 मिमी तथा मिमी है। पात्र का ऊपरी भाग वातावरण में खुला है।

पिस्टन को 5 मिमी/से की गति से धकेलने पर चंचू से बाहर वाली वायु की गति है
View Solutionएक छात्र ने u-v विधि से अवतल दर्पण की फोकस दूरी निकालने का प्रयोग किया। प्रयोग में उपयोग किये गये अवतल दर्पण की फोकस दूरी 24 cm तथा प्रकाशीय बैच की लम्बाई 1.5 m थी। प्रतिबिम्ब की स्थिति के निर्धारण में हुई अधिकतम त्रुटि 0.2 cm हो सकती है। छात्र द्वारा लिखे गये (u.v) के पांच मान (cm में) इस प्रकार थे. (42.56). (48.48). (60, 40). (66.33). (78.39)। (u.v) के मान जो प्रयोग के द्वारा प्राप्त नही हो सकते और गलत लिखे गये, वह है (वे हैं)
View Solutionएक कमरे में सप्लाई वोल्टेज 120 वोल्ट है Lead wires का प्रतिरोध 6Ω है । एक 60W का बल्ब पहले से ही जल रहा है । बल्ब के सिरों पर कितना वोल्टेज घटेगा जब बल्ब के समान्तर में लगे 240W के हीटर को चालू किया जाता है ?
View Solutionयंग के प्रयोग में दोनों रिलटो से पदों की दुरी 2 मीटर है 4800x 10^(-10)"मीटर"तरंगदैर्ध्य का प्रकाश उन पर आपतित होता है
यदि आपतित प्रकाश का तरंगदैर्द्य बदलकर कर दिया जाता है, तो फ्रेजो की चौड़ाई ज्ञात कीजिये
View Solutionजॉर्ज पंचम की नाक' पाठ के माध्यम से लेखक ने समाज पर क्या व्यंग्य किया है?
View Solution6328 Å तरंगदैर्ध्य का एक प्रकाश लम्बवत रूप से 0.2 mm चौड़ाई की झिरी पर आपतित होता है। परदे पर केंद्रीय उच्चिष्ठ की कोणीय चौड़ाई होगी
View Solutionकरुण रस की कविता जो किसी व्यक्ति की मृत्यु पर लिखी जाती है के लिए किस शब्द का प्रयोग किया जाता है ?
View Solutionटार्च बेचनेवाले" में टार्च के प्रतीक के माध्यम से लेखक ने किस पर प्रहार किया है ?
View Solutionरंगमंच पर पर्दे के पीछे का स्थान कहलाता है
View Solution(-1-1) और (4, 2) से समान दूरी पर स्थित बिन्दुओं के बिन्दुपथ का समीकरण है
View Solution5 बार और 300K पर एक आदर्श एक्परमाणविक गैस के दो मोल के 1 बार के ब्रह्म डाब तक अनुत्क्रमणीय रूप से प्रसारित किया जाता है गैस दवरा किया गया कार्य xR (बार लीटर में ) है x का मान है
View Solutionनाभिक से दूरी पर, अनंतसूक्ष्म मोटाई dr के गोलीय कोश में हाइड्रोजन परमाणु के 1s इलेक्ट्रॉन के पाए जाने की प्रायिकता P है। इस कोश का आयतन 4rr2 dr है। r पर P की निर्भरता का गुणात्मक रेखाचित्र है-
View Solutionजब धातु M को NaOH के साथ उपचारित किया जाता है, तो एक श्वेत जिलेटिन जैसा अवक्षेप 'X' प्राप्त होता है, जो NaOH के आधिक्य में घुलनशील होता है। यौगिक 'X' प्रबल रूप से गर्म करने पर एक ऑक्साइड देता है जिसका उपयोग वर्णलेखिकी में एक अधिशोषक के रूप में किया जाता है। धातु 'M' है:
View Solutionनिर्वात में इलेक्ट्रॉनों को त्वरित करके X-किरणों को उत्पन्न किया जा सकता है और एक धातु के पृष्ठ के परमाणुओं पर उन्हें आपतित किया जाता है। यदि इलेक्ट्रॉनों की 1000 ev गतिज ऊर्जा पूरी तरह से फोटॉन ऊर्जा में परिवर्तित हो जाती है। यदि इलेक्ट्रॉन धारा 1.5 xx 10^(-5) A है, तो 10^(-10) सेकंड में कितने फोटॉन उत्पन्न होते हैं?
View Solution
