यंग का द्वि - स्लिट प्रयोग 43अपवर्तनांक के माध्यम में किया जाता है | 600 नैनोमीटर तरंगदैर्ध्य का प्रकाश स्लिटों S1 व S2 पर जिनके बीच अंतराल 0.45 मिमी है, गिर रहा है | निचली स्लिट S2 काँच की पतली शीट से, जिसकी मोटाई 10.4 माइक्रोमीटर तथा अपवर्तनांक 1.5 है, ढकी गई है | व्यतिकरण प्रतिरूप, स्लिटों से 1.5 मी की दूरी पर रखे पर्दे पर देखा जाता है |
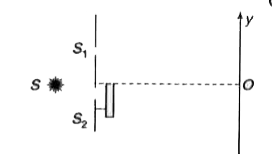
(a) Y- अक्ष पर केंद्रीय उच्चिष्ठ ( दीप्त फ्रिंज जिसके लिए पथांतर शून्य है ) की स्थिति ज्ञात कीजिए |
(b) बिंदु O पर, महत्तम फ्रिंज तीव्रता के सापेक्ष प्रकाश की तीव्रता ज्ञात कीजिए |
(c) अब यदि 600 नैनोमीटर के प्रकाश को 400 नैनोमीटर परास के श्वेत प्रकाश से बदल दिया जाए तो उस प्रकाश की तरंगदैर्ध्य ज्ञात कीजिए जो ठीक बिंदु पर उच्चिष्ठ बनाए (सभी तरंगदैर्ध्य, 4/3 अपवर्तनांक के दिए गए माध्यम के लिए हैं, विक्षेपण नगण्य हैं |)
The correct Answer is:(a) −4.33 मिमी (b) f=3lmax4 (c ) 650 नैनोमीटर; 433.33 नैनोमीटर
प्रश्नानुसार, λ=600 नैनोमीटर =6×10−7 मी,
d=0.45 मिमी =0.45×10−3 मी, D=1.5 मी
t=10.4 माइक्रोमीटर =10.4×10−6 मी
μm=4/3,μg=1.5
(a ) माना केंद्रीय उच्चिष्ठ बिंदु O के नीचे y दुरी पर है, तब
Δx1=S1P−S2P=ydD
काँच की चादर के कारण पथांतर,
Δx2=(μgμm−1)t
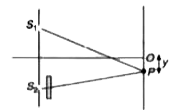
नेट पथांतर शून्य होगा जबकि Δx1=Δx2
या ydD=(μgμm−1)t
या y=(μgμm−1)tDd
मान प्रतिस्थापित करने पर,
y=(1.54/3−1)10.4×10−6(1.5)0.45×10−3
या y=4.33×10−3 मी =4.33 मिमी
(b ) बिंदु O पर, Δx1=0 तथा Δx2=(μgμm−1)t
∴ नेट पथांतर Δx=Δx2
∴ कलांतर, ϕ=2πλΔx
मान रखने पर
ϕ=2πu6×10−7(1.54/3−1)(10.4×10−6)=133π
अब I(ϕ)=Imaxcos2(ϕ2)
या I=Imaxcos2(13π6)
या I=34Imax
(c ) बिंदु O पर पथांतर,
Δx=Δx2=(μgμm−1)t
O पर अघिकतम तीव्रता के लिए
Δx=nλ (n=1,2,3,.....)
∴ λ=Δx1,Δx2,Δx3..... इत्यादि
Δx=(1.54/3−1)(1.04×10−6)
=1300 नैनोमीटर
∴ अधिकतम तीव्रता के लिए,
λ=1300nm,13002nm,13003nm,13004nm....
400 से 700 नैनोमीटर परास में तरंगदैर्ध्य 650 नैनोमीटर तथा 433.33 नैनोमीटर हैं|
Topper's Solved these Questions
- प्रकाशिकीBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रकाशिकीEXERCISE - श्रृंखलाबद्ध - बोधन प्रकार
5 Videos
- प्रकाशिकीBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रकाशिकीEXERCISE - एकल पूर्णांक उत्तर प्रकार
7 Videos
- पदार्थ के गुणBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - पदार्थ के गुणEXERCISE - शृंखलाबद्ध-बोधन प्रकार (अनुच्छेद-IV)
2 Videos
- प्रयोगात्मक भौतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रयोगात्मक भौतिकी EXERCISE - बहुविकल्पीय प्रश्न II
3 Videos
Similar Questions
चित्र में XY एक पृष्ठ है जो दो पारदर्शी माध्यमों, माध्यम -1 तथा माध्यम -2 को अलग करता है | रेखाएँ ab तथा cd माध्यम -1 में चल रहीं तथा पृष्ठ XY पर आपतित होने वाली प्रकाश - तरंग के तरंग्रागों को निरूपित करती हैं | रेखाएँ ef तथा gh अपवर्तन के बाद माध्यम -2 में चल रही प्रकाश तरंग के तरंग्रागों को निरूपित करती हैं |
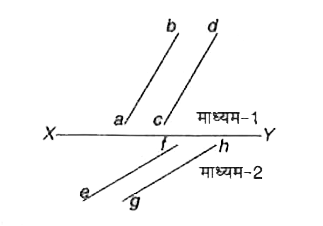
प्रकाश चल रहा ह
View Solutionएक पतले उभयोत्तल लेंस की फोकस दूरी 20 सेमी है | जब लेंस के सामने बिम्ब को 25 सेमी से 50 सेमी दूर ले जाया जाता है तो इसके प्रतिबिम्ब का आवर्धन m25 से n50 हो जाता है | m25m50 अनुपात का मान क्या होगा ?
View Solutionचित्र में दिखाई गयी पिचकारी में एक पिस्टन वायु को एक चंचू द्वारा बाहर धकेलता है। चंचू के सामने एकसमान अनुप्रस्थ-काट वाली पतली नली लगी है। नली का दूसरा सिरा द्रव से भरे एक छोटे पात्र में है। जब पिस्टन वायु को चंचू से बाहर धकेलता है, तब पात्र में द्रव उठकर चंचू में आ जाता है। ओर फुहार के रूप में बाहर निकलता है। चित्र में दिखाई गयी पिचकारी में पिस्टन तथा चंचू की त्रिज्याएँ क्रमशः 20 मिमी तथा मिमी है। पात्र का ऊपरी भाग वातावरण में खुला है।

पिस्टन को 5 मिमी/से की गति से धकेलने पर चंचू से बाहर वाली वायु की गति है
View Solutionएक छात्र ने u-v विधि से अवतल दर्पण की फोकस दूरी निकालने का प्रयोग किया। प्रयोग में उपयोग किये गये अवतल दर्पण की फोकस दूरी 24 cm तथा प्रकाशीय बैच की लम्बाई 1.5 m थी। प्रतिबिम्ब की स्थिति के निर्धारण में हुई अधिकतम त्रुटि 0.2 cm हो सकती है। छात्र द्वारा लिखे गये (u.v) के पांच मान (cm में) इस प्रकार थे. (42.56). (48.48). (60, 40). (66.33). (78.39)। (u.v) के मान जो प्रयोग के द्वारा प्राप्त नही हो सकते और गलत लिखे गये, वह है (वे हैं)
View Solutionएक परवलय की नाभि मूलबिंदु पर है तथा रेखा x=2 परवलय की नियता है , तो परवलय का शीर्ष है
View Solutionएकवर्णी प्रकाश का एक पुंज (beam of light) काँच की एक प्लेट पर 58^(@ के कोण पर आपतित होता है और परावर्तित किरणपुंज पूरी तरह समतल-ध्रुवित पाया जाता है। काँच का अपवर्तनांक निकालें।
View Solutionउस समतल का सदिश समीकरण जो बिन्दु A(4,7,−4) से जाता है तथा सदिश (3,2,−1)पर लम्ब है -
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solutionजॉर्ज पंचम की नाक' पाठ के माध्यम से लेखक ने समाज पर क्या व्यंग्य किया है?
View Solutionव्यतिकरण|यंग का स्लिट प्रयोग
View Solutionयंग का द्वि स्लिट प्रयोग
View Solutionयंग का द्वि- स्लिट प्रयोग#!#यंग का एकल झिरी प्रयोग
View Solutionयंग का द्वि-स्लिट प्रयोग#!#विवर्तन
View Solutionकरुण रस की कविता जो किसी व्यक्ति की मृत्यु पर लिखी जाती है के लिए किस शब्द का प्रयोग किया जाता है ?
View Solution
