दो पारदर्शी माध्यमों के बीच परिसीमा x−y तल हैं | माध्यम −1, जिसके लिए z≥0 का अपवर्तनांक √2 है तथा माध्यम −2, जिसके लिए z≤0 का अपवर्तनांक √3 है | माध्यम −1 में वेक्टर A=6√3ˆi+8√3ˆj−10ˆk द्वारा निरूपित प्रकाश की किरण पृथक्कारी तल पर आपतित होती है | माध्यम -2 में अपवर्तित किरण की दिशा में एकांक वेक्टर ज्ञात कीजिए |
The correct Answer is:15√2(3ˆi+4ˆj−5ˆk)
आपतित कोण
A=6√3ˆi+8√3ˆj−10ˆk
=(6√3ˆi+8√3ˆj)+(−10ˆk)
=QO+PQ (चित्रानुसार)
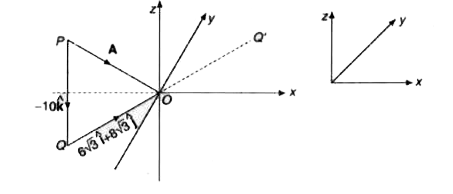
QO, xy - तल में स्थित हैं|
QQ' तथा Z - अक्ष परस्पर लंबवत हैं| अतः उन्हें द्वी - विमीय आकृति में दिखा सकता है|
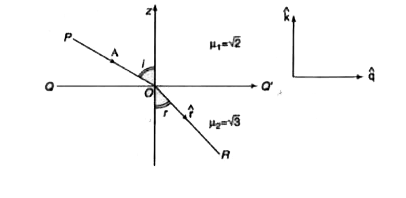
Z - अक्ष से A द्वारा बनाया गया कोण
i=cos−1⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩10√(10)2+(6√3)2+(8√3)2⎫⎪
⎪
⎪
⎪⎬⎪
⎪
⎪
⎪⎭=cos−1{12}
या i=60∘
QOQ' दिशा में एकांक वेक्टर,
ˆq=6√3ˆi+8√3ˆj√(6√3)2+(8√3)2=15(3ˆi+4ˆj)
स्नैल के नियम से, √3√2=sinisinr=sin60∘sinr
∴ sinr=√3/2√3/√2=1√23
∴ r=45∘
अब हमें अपवर्तित किरण की दिशा OR में एकांक वेक्टर ज्ञात करना है, माना यह ˆr है जिसका परिमाण 1 तब
ˆr=(1sinr)ˆq−(1cosr)ˆk
=1√2[ˆq−ˆk]
=1√2[15(3ˆi+4ˆj)−ˆk]
या ˆr=15√2(3ˆi+4ˆj−5ˆk)
Topper's Solved these Questions
- प्रकाशिकीBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रकाशिकीEXERCISE - श्रृंखलाबद्ध - बोधन प्रकार
5 Videos
- प्रकाशिकीBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रकाशिकीEXERCISE - एकल पूर्णांक उत्तर प्रकार
7 Videos
- पदार्थ के गुणBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - पदार्थ के गुणEXERCISE - शृंखलाबद्ध-बोधन प्रकार (अनुच्छेद-IV)
2 Videos
- प्रयोगात्मक भौतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रयोगात्मक भौतिकी EXERCISE - बहुविकल्पीय प्रश्न II
3 Videos
Similar Questions
चित्र में XY एक पृष्ठ है जो दो पारदर्शी माध्यमों, माध्यम -1 तथा माध्यम -2 को अलग करता है | रेखाएँ ab तथा cd माध्यम -1 में चल रहीं तथा पृष्ठ XY पर आपतित होने वाली प्रकाश - तरंग के तरंग्रागों को निरूपित करती हैं | रेखाएँ ef तथा gh अपवर्तन के बाद माध्यम -2 में चल रही प्रकाश तरंग के तरंग्रागों को निरूपित करती हैं |
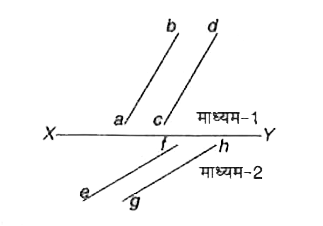
प्रकाश चल रहा ह
View Solutionएक पतले उभयोत्तल लेंस की फोकस दूरी 20 सेमी है | जब लेंस के सामने बिम्ब को 25 सेमी से 50 सेमी दूर ले जाया जाता है तो इसके प्रतिबिम्ब का आवर्धन m25 से n50 हो जाता है | m25m50 अनुपात का मान क्या होगा ?
View Solutionचित्र में दिखाई गयी पिचकारी में एक पिस्टन वायु को एक चंचू द्वारा बाहर धकेलता है। चंचू के सामने एकसमान अनुप्रस्थ-काट वाली पतली नली लगी है। नली का दूसरा सिरा द्रव से भरे एक छोटे पात्र में है। जब पिस्टन वायु को चंचू से बाहर धकेलता है, तब पात्र में द्रव उठकर चंचू में आ जाता है। ओर फुहार के रूप में बाहर निकलता है। चित्र में दिखाई गयी पिचकारी में पिस्टन तथा चंचू की त्रिज्याएँ क्रमशः 20 मिमी तथा मिमी है। पात्र का ऊपरी भाग वातावरण में खुला है।

पिस्टन को 5 मिमी/से की गति से धकेलने पर चंचू से बाहर वाली वायु की गति है
View Solutionएक छात्र ने u-v विधि से अवतल दर्पण की फोकस दूरी निकालने का प्रयोग किया। प्रयोग में उपयोग किये गये अवतल दर्पण की फोकस दूरी 24 cm तथा प्रकाशीय बैच की लम्बाई 1.5 m थी। प्रतिबिम्ब की स्थिति के निर्धारण में हुई अधिकतम त्रुटि 0.2 cm हो सकती है। छात्र द्वारा लिखे गये (u.v) के पांच मान (cm में) इस प्रकार थे. (42.56). (48.48). (60, 40). (66.33). (78.39)। (u.v) के मान जो प्रयोग के द्वारा प्राप्त नही हो सकते और गलत लिखे गये, वह है (वे हैं)
View Solutionध्वनि संचरण के लिए माध्यम की आवश्यकता होती है
View Solutionसंचार के मुद्रण माध्यम में किसे शामिल किया जाता है?
View Solutionसाहित्यिक अभिव्यक्ति में रचनात्मक लेखन का माध्यम है
View Solutionसंचार के मुद्रण माध्यम में किसे शामिल किया जाता है ?
View Solutionसाहित्यिक अभिव्यक्त्ति में रचनात्मक लेखन का माध्यम है
View Solutionछोटे बालको की कल्पनाशक्ति विकसित करने का माध्यम है
View Solutionध्वनि संचरण के लिए माध्यम की आवश्यकता
View Solutionधातु केंद्र के जलीय परमैंगनेट आयन में अपचयन के दौरान क्या सम्मिलित होता हैं
(1) 5 इलेक्ट्रॉन, उदासीन माध्यम में
(2) 5 इलेक्ट्रॉन, अम्लीय माध्यम में
(3) 3 इलेक्ट्रॉन, उदासीन माध्यम में
(4) 3 इलेक्ट्रॉन, क्षारीय माध्यम में
View Solutionअम्लीय माध्यम में, मोहर लवण और Fe2(SO4)3 के मिश्रण के 4 मोल के पूर्ण ऑक्सीकरण के लिए 1 M, K2Cr2O7 के 500 ml की आवश्यकता होती है। मिश्रण में मोहर लवण का मोल% है:
View Solutionनिम्नलिखित कथ्नों के लिए सही विकल्न का चयन कीजिए। 1. Cl_(2)O और ClO_(2) का उपयोग विरंजन कारक के रूप में किया जाता है। 2. OCl^(-) लवण का उपयोग अपमार्जक के रूप में किया जाता है। 3. OCl^(-) क्षारीय माध्यम में विततानुपातित हो जाता है। 4. BrO_(3)^(-) अम्लीय माध्यम में ऑक्सीकृत होता है।
View Solutionअम्लीय माध्यम में H_2O_2, Cr_2O_(7)^(-2) को CrO_5 में परिवर्तित करता है, जिसमें दो (-O-O) बंध होते हैं। CrO_5 में Cr की ऑक्सीकरण अवस्था है :
View Solutionजलीय माध्यम में विलेयता के सही क्रम की पहचान कीजिए
View Solution
