माना दीर्घवृत्त x29+y25=1 की नाभियाँ (foci) (f1,0) और (f2,0) हैं, जहाँ f1>0 और f2<0 हैं। माना P एवं 2 दो परवलय (parabola) हैं। जिनकी नाभियाँ क्रमश: (f1,0) एवं (2f2,0) हैं तथा दोनों के शीर्ष (vertex) (0, 0) है। माना P की स्पर्श रेखा 7, बिन्दु (2f2,0) से एवं P2 की स्पर्श रेखा T2 बिन्दु (f1,0) से गुजरती हैं। यदि T1 की प्रवणता (slope) m1 हो और T2 की प्रवणता m2 हो, तब (1m21+m22) का मान है।
The correct Answer is:1m21+m22=4
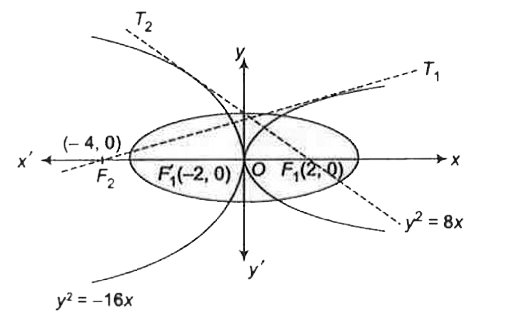
y2=−16x
P1 के सापेक्ष स्पर्शी रेखा जो (2f2,0) अर्थार्त (−4,0) से होकर गुजरती है
∴T1:y=m1x+2m1
⇒0=−4m1+2m1
⇒m21=1/2.......(i)
साथ ही P2 के सापेक्ष स्पर्शी रेखा जो (f1,0) अर्थार्त (2,0) से होकर गुजरती है
⇒T2:y=m2x+(−4)m2⇒0=2m2−4m2
⇒m22=2......(ii)
∴1m21+m22=2+2=4
Topper's Solved these Questions
- परवलयBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - परवलयEXERCISE - विश्लेषणात्मक प्रश्न
12 Videos
- निश्चित समाकलन BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - निश्चित समाकलन EXERCISE - एकल पूर्णाक प्रश्न
7 Videos
- प्रतिलोम वृत्तीय फलन BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रतिलोम वृत्तीय फलन EXERCISE - एकल पूर्णांक प्रश्न
1 Videos
Similar Questions
माना परवलय Y2=4x के तीन भिन्न बिन्दुओं पर खींचे गए अभिलम्ब, बिन्दु (h, 0) से होकर जाते हैं। दिखाइए कि h का मान 2 से अधिक है।
View Solutionदिया है कि किसी वास्तविक संख्या x के लिए [x], अधिकतम पूर्णांक को दर्शाता है यदि अन्तराल [−10,10] पर वास्तविक मानों वाला फलन f निम्न प्रकार से परिभाषित है f(x)={x−[x],if [x] is Odd,1+[x]−x, if [x] is Even तो π210∫10−10f(x)cosπxdx का मान है
View Solutionमाना f:[0,4π]→[0,π],f(x)=cos−1(cosx) के द्वारा परिभाषित है। तब x∈[0,4π] में समीकरण f(x)=10−x10 को संतुष्ट करने वाले बिंदुओं की संख्या है
View SolutionSuppose that the foci of the ellipse x29+y25=1 are (f1,0)and(f2,0) where f1>0andf2<0. Let P1andP2 be two parabolas with a common vertex at (0,0) and with foci at (f1,0)and(2,f20), respectively. Let T1 be a tanent to P1 which passes through (2f2,0) and T2 be a tangent to P2 which passes through (f1,0). If m1 is the slope of T1andm2 is the slope of T2, then the value of (1m21+m22) is __________
View SolutionLet f(1):R→R,f2:[0,∞)→R,f3:R→Randf4:R→[0,∞) be a defined by
f1(x)={|x|if x<0exif x>0:f2(x)=x2,f3(x)={sinxif x<0xif x≥0 and f4(x)={f2(f1(x))if x<0f2(f1(f1(x)))−1if x≥0 Then, f4 is
View SolutionSuppose that the foci of the ellipse x29+y25=1 are (f1,0)and(f2,0) where f1>0andf2<0 Let P1andP2 be two parabola with a c ommon vertex at (0, 0) and with foci at (f1,0)and(2fz,0) and T2 be a tangent to P2 which passes through (f1,0). If m1 is the slope of T1andm2 is the slope of T2, then the value of (1m21+m22), is
View Solution''स्तम्भ'अ'''''स्तम्भ'ब'''बिन्दु(−4,5)एवं(4,−5)के मध्य-बिन्दु के निर्देशांकy(0,3)एवं(4,0)के बीच की दुरी (x)मूल बिन्दु से(x,y)के बीच की दुरी0,0(0,y) बिन्दु की कोटि 5(x,0) बिन्दु की भुज√x2+y2
View Solutionl+(f1−f02f1−f0−f2)×hसूत्र है:
View Solutionबहुलक =l+(f1−f02f1−f0−f2)×h में h होता है ।
View SolutionSuppose that the foci of the ellipse x29+y25=−1 are (f1,0) and (f2,0) where f1>0 and f2<0. Let P1 and P2 be two parabolas with a common vertex at (0, 0) and with foci at (f1,0) and (2f2,0) respectively. Let T1 be a tangent to P1 which passes through (2f2,0) and T2 be a tangent to P2 which passes Through (f1,0). If m1 is the slope of T1 and m2 is the slope of T2, then the value of (1m21+m22) is -
View Solutionपरवलय y2=2x की स्पर्श रेखा 18x-6y+1= 0 का स्पर्श बिन्दु है
View Solutionबिन्दु (2, 3) से जाने वाली, दीर्घवृत्त 9x2+16y2=144 की स्पर्श रेखाओं के समीकरण हैं
View Solution(A) (B)1. समचतुर्भुज के विकर्ण होते हैं(a) अद्वितीय हल2. त्रिभुज की दो भुजाएँ बराबर होतीए हैं(b) लंबवत3. बहुलक(c) समद्विबाहु त्रिभुज4. प्रायिकता(d) l1+(f1−f0)2f1−f0−f2×(l2−l1)5. रेखाएँ प्रतिच्छेदी हो(e) n(A)n(S)
View SolutionF(x) को दो वास्तविक फलनों f1(x),x∈IR, तथा f2(x)={sin1xयदिx≠00यदिx=0
के गुणनफल के रूप में निम्न प्रकार | 0, यदि x = 0 है से परिभाषित कीजिये F(x)={f1(x)f2(x)यदिx≠00यदिx=0
कथन-1: Fx, IR पर सतत् है।
कथन-2 : f1(x) तथा f2(x) , IR पर सतत् है।
View Solutionमाना कि दीर्घ वृत x29+y25=1 की नाभियाँ (f1,0) और (f2,0) हैं, जहाँ f1>0 और f2<0 हैं। माना कि P1 एवं P2 दो परवलय हैं जिनकी नाभियाँ क्रमशः (f1,0) एवं (2f2,0) हैं तथा दोनों के शीर्ष (vertex) (0,0) है। माना कि P1 की स्पर्श रेखा T1 बिन्दु (2f2,0) से, एवं P2 की स्पर्श रेखा T2 बिन्दु (f1,0) से गुजरती हैं। यदि T1 की प्रवणता m1 हो और T2 की प्रवणता m2 हो, तब (1m21+m22) का मान ज्ञात करो ।
View Solution
