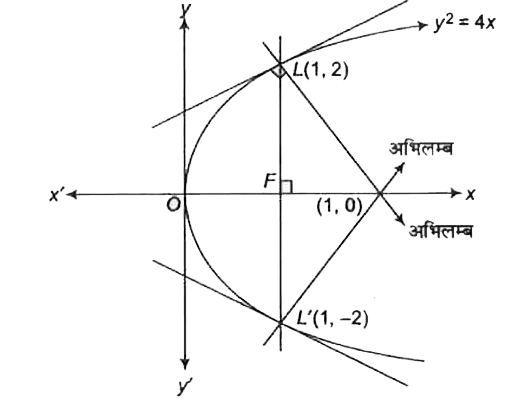
यदि परवलय (parabola) y2=4x के नाभिलम्ब जीवा (latusrectum) के शिखर बिन्दुओं पर खींचे गए अभिलम्ब (normals) वृत्त (x−3)2+(y+2)2=r2 की स्पर्श रेखाएँ हैं, तब r2 का मान है।
The correct Answer is:r2=2
नाभिलम्ब के सिरे बिंदु (a,±2a) अर्थार्त (1,±2) है| (x1,y1) पर अभिलम्ब की समीकरण होगी y−y1x−x1=−y12a
अर्थार्त y−2x−1=−22 तथा x−y=3
जोकि (x−3)2+(y+2)2=r2 पर स्पर्शी है
केंद्र से लम्ब की लम्बाई =त्रिज्या
⇒|3−2−3|√12+12=r
r2=2
Topper's Solved these Questions
- परवलयBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - परवलयEXERCISE - विश्लेषणात्मक प्रश्न
12 Videos
- निश्चित समाकलन BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - निश्चित समाकलन EXERCISE - एकल पूर्णाक प्रश्न
7 Videos
- प्रतिलोम वृत्तीय फलन BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रतिलोम वृत्तीय फलन EXERCISE - एकल पूर्णांक प्रश्न
1 Videos
Similar Questions
माना परवलय Y2=4x के तीन भिन्न बिन्दुओं पर खींचे गए अभिलम्ब, बिन्दु (h, 0) से होकर जाते हैं। दिखाइए कि h का मान 2 से अधिक है।
View Solutionदिया है कि किसी वास्तविक संख्या x के लिए [x], अधिकतम पूर्णांक को दर्शाता है यदि अन्तराल [−10,10] पर वास्तविक मानों वाला फलन f निम्न प्रकार से परिभाषित है f(x)={x−[x],if [x] is Odd,1+[x]−x, if [x] is Even तो π210∫10−10f(x)cosπxdx का मान है
View Solutionमाना f:[0,4π]→[0,π],f(x)=cos−1(cosx) के द्वारा परिभाषित है। तब x∈[0,4π] में समीकरण f(x)=10−x10 को संतुष्ट करने वाले बिंदुओं की संख्या है
View Solutionएक परवलय के नाभिलम्ब का समीकरण x+y=8 तथा उसके शीर्ष पर स्पर्शी का समीकरण x+y=12 है, तो उसके नाभिलम्ब की लम्बाई है :
View Solutionयदि किसी बिंदु P के परवलय y2=4x पर खींची गई दो स्पर्श-रेखाएँ परस्पर लम्ब हों, तो P का बिन्दुपथ है :
View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
View Solutionयदि बिन्दु (1, 2) से वृत्त x2+y2−2x−4y+λ=0 पर असंख्य स्पर्श रेखाएं खींची जा सकती हों, तो λ का मान है।
View Solutionवृत्त x2+y2=169 के बिन्दुओं (5, 12) तथा (12,-5) पर खींची गई स्पर्श रेखाओं के बीच का कोण है
View Solutionउन बिन्दुओं को मिलाने वाली जीवा की लम्बाई, जिन पर सरल रेखा x3+y4=1 , वृत्त x2+y2=16925 को काटती है, है
View Solutionपरवलय y2=4ax की, उन जीवाओं के मध्य बिन्दुओं का बिन्दुपथ जो मूल बिन्दु से होकर जाती हैं, होगा
View Solutionपरवलय y2=4ax के बिन्दु (a4,a) पर अभिलम्ब का समीकरण है
View Solutionयदि रेखा 2x + y + k = 0 परवलय y2=−8x पर अभिलम्ब हो, तो k का मान होगा
View Solutionपरवलय y2=4ax की स्पर्श रेखा पर नाभि से डाले गये लम्ब के पाद का बिन्दुपथ है
View Solutionपरवलय y2=4ax के नाभिलम्ब के सिरे पर खींची गयी स्पर्श रेखाओं के बीच का कोण होगा
View Solutionपरवलय y2=4a(x−a) पर मूलबिन्दु से खींची गयी स्पर्श रेखाओं के बीच का कोण है
View Solutionमाना एक वृत्त है जिसका केन्द्र परवलय y2=2px की नाभि पर है, तथा यह वृत्त परवलय की नियता को स्पर्श करता है, तो वृत्त व परवलय का प्रतिच्छेद बिंदू है
View Solution
