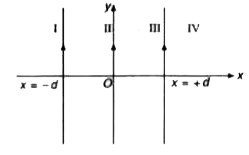
तीन अनन्त लम्बे पतले तार, जिनमें से प्रत्येक में धारा । एक ही दिशा में बह रही है, गुरुत्व मुक्त स्थान में - तल में स्थित हैं। बीच का तार Y-अक्ष के अनुदिश है जबकि अन्य दो x = d के अनुदिश हैं।
(a) ऐसे बिन्दुओं का बिन्दु पथ ज्ञात कीजिए, जहाँ चुम्बकीय क्षेत्र B शून्य हो।
(b) यदि बीच के तार को 7-अक्ष की दिशा में थोड़ा-सा विस्थापित करके छोड़ दिया जाये तो दिखाइये कि यह सरल आवर्त गति करेगा, यदि तारों का रैखिक घनत्व (Linear density)λ है, तो स्पंदन की आवृत्ति क्या है?
(1997,5M)
The correct Answer is:x=0=z z=0 x=±d√3, f=i2πd√μ0πλ
(a) y-अक्ष पर चुम्बकीय क्षेत्र शून्य होगा, अर्थात्
x = 0 = z
क्षेत्रों I तथा IV में चुम्बकीय क्षेत्र शून्य नहीं हो सकता क्योंकि क्षेत्र । में चुम्बकीय क्षेत्र +z दिशा में होगा (तीनों तारों के कारण), जबकि इन्हीं तीनों तारों के कारण क्षेत्र IV में चुम्बकीय क्षेत्र-2 अक्ष के अनुदिश होगा। चुम्बकीय क्षेत्र केवल क्षेत्र II तथा II में शून्य हो सकता है।
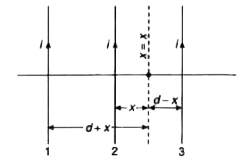
माना रेखा z = 0 तथा x = x पर चुम्बकीय क्षेत्र शून्य है, तब तारों 1 व 2 के कारण इस रेखा पर चुम्बकीय क्षेत्र -- अक्ष के अनुदिश होगा तथा तार 3 के कारण यह +z अक्ष के अनुदिश होगा।
B1+B2=B3
μ02πid+x+μ02πix=μ02πid−x
x=−+d√3
जहाँ चुम्बकीय क्षेत्र शून्य है।
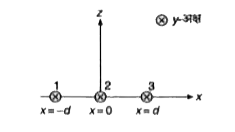
(b) इस भाग में हम निर्देशांक अक्षों को परिवर्तित करेंगे। (केवल सुविधा के लिए)
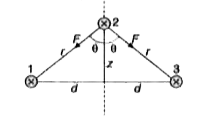
तीन तार 1,2 व 3 चित्रानुसार व्यवस्थित हैं। यदि हम तार 2 को z-अक्ष की ओर विस्थापित करें, तो तार-युग्मों (1 तथा 2) और (2 तथा 3) के बीच एकांक लम्बाई पर कार्यरत् आकर्षण बल,
x-अक्ष के अनुदिश F के घटक निरस्त हो जाएगे। कुल परिणामी बल -2-अक्ष के अनुदिश होगा, जिसका मान
Fnet=μ0i22πr(2cosθ)=2{μ0i22πr}zr
यदि z<z2+d2=d2
Fnet=−(μ0i2πd2)(z) .............(i)
ऋण चिन्ह बल F की प्रत्यानयन प्रकृति को दर्शाता है।
∴Fnet∝−Z, अर्थात् तार सरल आवर्त गति करेगा।
माना इस अवस्था में तार का त्वरण व है तथा तार के एकांक लम्बाई का द्रव्यमान m है, तब Fnet=λ⋅a=−(μ0I2πd2)z
a = -(μ0I2πd2)z
∴ दोलनों की आवृत्ति
f=12π√त्वरण/विस्थापन
12π√az=12π⋅id√μ0πλ
f = i2πd√μ0πλ
Topper's Solved these Questions
- चुम्बकत्व BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - चुम्बकत्व EXERCISE - श्रृंखलाबद्ध-बोधन प्रकार (अनुच्छेद।)
2 Videos
- चुम्बकत्व BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - चुम्बकत्व EXERCISE - श्रृंखलाबद्ध-बोधन प्रकार (अनुच्छेद ii )
2 Videos
- चुम्बकत्व BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - चुम्बकत्व EXERCISE - एकल पूर्णांक उत्तर प्रकार
5 Videos
- घूर्णन गतिBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - घूर्णन गतिEXERCISE - श्रृंखलाबद्ध बोधन प्रकार
10 Videos
- तरंगे BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - तरंगे EXERCISE - श्रंखलाबद्ध - बोधन प्रकार (अनुच्छेद III )
2 Videos
Similar Questions
X-Y तल में R त्रिज्या की वृत्तीय कक्षा में एक बिन्दु आवेश ω कोणीय गति से परिक्रमा कर रहा है। इसे लूप में बहती हुई Qω2π अपरिवर्ती धारा के तुल्य माना जा सकता है। अब एकसमान च्बकीय क्षेत्र को धनात्मक :-दिशा में चालू करते हैं जिसका मान 0 से B तक एक सेकण्ड में एकसमान दर से बढ़ता है। यह मानिए कि इस दौरान कक्ष की त्रिज्या स्थिर रहती है। चुम्बकीय क्षेत्र के लगाने से कक्ष में एक emf प्रेरित होता है। एक प्रेरित विद्युत क्षेत्र द्वारा इकाई धन आवेश को संवृत्त लूप के चारों ओर घुमाने में किए गए कार्य की मात्रा को प्रेरित विद्युत वाहक बल (emf) कहा जाता है। यह ज्ञात है कि जब एक आवेश एक कक्ष में परिभ्रमण करता है तब उसका चुम्बकीय द्विध्रुव आघूर्ण उसके कोणीय संवेग के अनुपातिक होता है जिसका अनुपातिक स्थिरांक γ है।
Q चुम्बकीय क्षेत्र के परिवर्तन के दौरान कक्ष में किसी विशेष क्षण पर प्रेरित विद्युत क्षेत्र का मान है
View Solutionचित्र में दर्शाये गये, α त्रिज्या वाला वृत्तीय पाश (Loop) तथा दो समान्तर तार अंकित 1 तथा 2 सभी पृष्ठ के तल में हैं। दोनों तार वृत्तीय पाश के केन्द्र से d दूरी पर हैं। वृत्तीय पाश तथा दोनों तारों में एकसमान धारा | प्रवाहित है। ऊपर से देखने पर वृत्तीय पाश में धारा की दिशा वामावर्त है।
Q जब d≅a लेकिन तार पाश को स्पर्श नहीं कर रहे हैं तब वृत्तीय पाश के अक्ष पर ऊँचाई पर परिणामी चुम्बकीय क्षेत्र शून्य मिलने की स्थिति में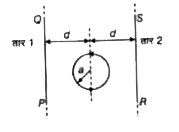
View Solutionएक स्थिर विद्युत धारा I समकोण त्रिभुजाकार लूप POR में प्रवाहित हो रही है। इस त्रिभुज की भुजाओं की लम्बाई, क्रमशः PQ = 3x, PR = 4x तथा QR = 5x है। बिन्दु P पर लूप से उत्पन्न चुम्बकीय क्षेत्र का मान k (μ0I48πx) है k का मान ज्ञात कीजिए।
View Solutionदो डिस्कें A तथा B एक ऊर्ध्वाधर धुरी पर समाक्ष रूप से अवस्थिरत की गई है। उभयनिष्ठ अक्ष के परितः उन चकतियों के जड़त्व आघूर्ण क्रमशः I तथा 2I है। एक स्पि्रंग को x1 दूरी से दबाकर उसकी सम्पूर्ण स्थितिज ऊर्जा का उपयोग करके, चकती A को प्रारंभिक कोणीय वेग 2ω दिया जाता है। उतने ही स्पि्रंग गुणांक वाले एक दूसरे स्पि्रंग को x2 दूरी से दबाकर डिस्क B को कोणीय वेग ω दिया जाता है। दोनों चकतियां दक्षिणावर्त दिशा में घूम रही हैं
अनुपात x1/x2 है।
View Solutionअधिकतर पदार्थो का अपवर्तनांक, n>1 होता है। इसलिये जब कोई प्रकाश किरण वायु से किसी प्राकृतिक पदार्थ में प्रवेश करती है तब, Snell's नियम, sinθ1sinθ2=n2n1के अनुसार, अपवर्तित किरण अभिलंब की तरफ झुकती है। लेकिन यह कभी भी अभिलंब के आपतित किरण वाले ओर से बाहर नहीं निकलती। विद्युत-चुम्बकत्व के अनुसार, किसी माध्यम का अपवर्तनांक n=(cv)=±√εrμr, होता है, जहाँ C विद्युत – चुम्बकीय तरंगों की निर्यात में चाल तथा v उनकी माध्यम में चाल हैं, εr व μr क्रमशः माध्यम की सापेक्ष विद्युतशीलता व चुंबकशीलता हैं। आम पदार्थों में εr व μr दोनों धनात्मक होते हैं, अर्थात माध्यम का n धनात्मक है। जब εr व μr दोनों ऋणात्मक हों तब हमें n का ऋणात्मक वर्गमूल लेना होगा। ऐसे ऋणात्मक n वाले पदार्थ अब अप्राकृतिक रूप में तैयार किये जा सकते हैं, और उन्हें मैटा-पदार्थ (meta-metarial) कहते हैं। वे बिलकुल अलग तरह का प्रकाशिक गुणधर्म दर्शाते हैं, परंतु भौतिक नियमों का उल्लंघन नहीं करते। चूँकि n ऋणात्मक है, अपवर्तित प्रकाश की चलने की दिशा में परिवर्तन होता है। तथापि आम पदार्थों की तरह इन मैटा-पदार्थों में भी अपवर्तन पर प्रकाश की आवृत्ति नहीं बदलती।
सही प्रकथन चुनें।
View Solutionएक लम्बे सीधे तार में बहने वाली धारा 1 ऐम्पियर है। चुंबकीय क्षेत्र की तीव्रता 10−5 वेबर/मीटर2 होगी तार से :
View Solutionएक वैद्युत तथा चुम्बकीय तरंग किसी माध्यम में वेग vecV = v, से जा रही है। वैद्युत-चुम्बकीय तरंग के वैद्युत दोलन Y-अक्ष के अनुदिश हैं। (i) चुम्बकीय क्षेत्र के दोलन किस दिशा में हो रहे होंगे ? (ii) वैद्युत क्षेत्र तथा चुम्बकीय क्षेत्र के परिमाण परस्पर किस प्रकार सम्बन्धित होंगे?
View Solutionकोई रेखा x-अक्ष और y-से साथ क्रमशः 60∘ तथा 45∘ के कोण बनाती है। इनके द्वारा घनत्व दिशा में z-अक्ष के साथ कितना कोण बनेगा ?
View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
View Solutionएक परवलय का अक्ष X-अक्ष के अनुदिश है। यदि इसके शीर्ष तथा नाम नाभि , X-अक्ष कि धनात्मक दिशा में मूलबिंदु से क्रमशः 2 तथा 4 कि दुरी पर हैं , तो इनमें से कौन - सा बिन्दु इस परवलय पर स्थित नहीं है ?
View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
View Solutionनिम्न में से कौन-सा कथन सत्य हैं ?
"tan A का मान सदैव-1 और 1 के बीच होता है।"
View Solutionनिम्न में से कौन-सा कथन सत्य हैं ?
"sec A का मान-1 और 1 के बीच में होता है
View Solutionयदि एक कण पर क्रिया करते हुए तीन बल संतुलन में हैं। पहले दो के बीच का कोण 90∘, ... दूसरे और तीसरे के बीच का कोण 120∘ हैं, तो बलों का अनुपात ज्ञात कीजिए।
View Solutionकॉलम - I में कुछ निश्चित स्थितियां दी गई है जिनमे प्रतिरोध का सीधा धात्विक तार प्रयुक्त किया है तथा कॉलम - II में कुछ परिणामी प्रभाव दिए है कॉलम - I के कथनो को कॉलम - II के कथनो से सुलमित कीजिए
कॉलम - I कॉलम - II(A)एक आवेशित संधारित्र को तार के सिरों से जोड़ा गया है(p) एक नियत धारा तार में से प्रवाहित होती है(B)तार को इसकी लम्बाई के लम्बवत नियत वेग से एक समान चुम्बकीय क्षेत्र में गतिमान किया जाता है चुम्बकीय क्षेत्र गति के तल के लम्बवत है(q)उष्मीय ऊर्जा तार में उत्पन्न होती है(C)तार को नियत विधुत क्षेत्र में रखा जाता है जिसकी दिशा तार की लम्बाई के अनुदिश है(r)तार के सिरों पर एक नियत विभवान्तर उत्पन्न होता है(D)तार के सिरों पर एक नियत वि. वा. बल. की बैट्री जोड़ी जाती है(s)तार के सिरों का नियत परिमाण का आवेश उपस्थित होता है
View SolutionAmpere has given a theory to find the magnetic field due to current distribution. in loop धारा I_(3) के चुम्बकीय क्षेत्र में अंशदान को नहीं लेते है क्योंकि चुम्बकीय क्षेत्र पुरे लूप मे युग्मित है। एक समाक्षीय केबिल में तार की त्रिज्या a है , इसके चारो ओर के बेलनाकार सेल की आंतरिक व बाह्य त्रिज्याएँ क्रमशः b तथा c है। अंदर वाले तार में i ऐम्पियर धारा बहती है तथा बाहरी सेल में बराबर व विपरीत धारा बहती है। अक्ष से x दूरी ( x lt a) पर चुंबकीय क्षेत्र है
View Solution
