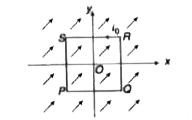
एक एकसमान, नियत चुम्बकीय क्षेत्र B, X- तल में X-अक्ष से 45° के कोण पर दिष्ट है। PORS एक दृढ़ वर्गाकार तार का फ्रेम है जिसमें स्थायी धारा बह रही है तथा जिसका केन्द्र मूल बिन्दु० पर है। क्षण = 0 पर फ्रेम दिखाई गई स्थिति में विरामावस्था में है तथा इसकी भुजायें x वY-अक्षों के समान्तर हैं। फ्रेम की प्रत्येक भुजा का द्रव्यमान m है तथा लम्बाई L है।
(a) चुम्बकीय क्षेत्र के कारण फ्रेम पर केन्द्र के परितः लगने वाला बल-आघूर्ण τ क्या है?
(b) वह कोण ज्ञात कीजिए जिससे फ्रेम इस बल आघूर्ण के अन्तर्गत एक सूक्ष्म समयान्तराल △t में घूम जाता है तथा वह अक्ष भी ज्ञात कीजिए जिसके परितः फ्रेम घूमता है। (△t इतना सूक्ष्म है कि समयान्तराल के दौरान बल-आघूर्ण में परिवर्तन नगण्य है)। फ्रेम के तल के लम्बवत् केन्द्र से गुजरने वाली अक्ष के परितः फ्रेम का जड़त्व आघूर्ण 43mL2 है।
The correct Answer is:(a) |τ|=i0L2B ,(b) θ=34i0BM(Δt)2
लूप का चुम्बकीय आघूर्ण, M =(iA)ˆk
(i0L2)ˆk
चुम्बकीय क्षेत्र, B = (B cos 45∘ˆi + (Bsin 45∘)ˆj
B√2(ˆi+ˆj) (a) लूप पर कार्यरत् बल आघूर्ण,τ=M×B
= (i0L2ˆk)×[B√2(ˆi+ˆj)]
या |τ|=i0L2B
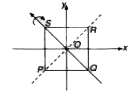
(b) घूर्णन अक्ष, बल आघूर्ण के संपाती है तथा बल आघूर्ण 1-1 दिशा में है या OS के समान्तर है। अत: लूप तथा S से जाने वाली अक्ष के परितः चित्रानुसार घूर्णन करेगा।
कोणीय त्वरण, α=|τ|I जहाँ, I = Qs के परितः लूप का जड़त्व आघूर्ण,
IQS+IPR=IZ
परन्तु IQS=IPR
2IQS=IZ=43ML2
α|τ|I = i0L2B2/3ML2=3i0B2M
इसलिए समय में फ्रेम द्वारा घूमा गया कोण,
θ=12α(△t)2
θ=34i0B4M⋅(△t)2
Topper's Solved these Questions
- चुम्बकत्व BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - चुम्बकत्व EXERCISE - श्रृंखलाबद्ध-बोधन प्रकार (अनुच्छेद।)
2 Videos
- चुम्बकत्व BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - चुम्बकत्व EXERCISE - श्रृंखलाबद्ध-बोधन प्रकार (अनुच्छेद ii )
2 Videos
- चुम्बकत्व BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - चुम्बकत्व EXERCISE - एकल पूर्णांक उत्तर प्रकार
5 Videos
- घूर्णन गतिBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - घूर्णन गतिEXERCISE - श्रृंखलाबद्ध बोधन प्रकार
10 Videos
- तरंगे BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - तरंगे EXERCISE - श्रंखलाबद्ध - बोधन प्रकार (अनुच्छेद III )
2 Videos
Similar Questions
X-Y तल में R त्रिज्या की वृत्तीय कक्षा में एक बिन्दु आवेश ω कोणीय गति से परिक्रमा कर रहा है। इसे लूप में बहती हुई Qω2π अपरिवर्ती धारा के तुल्य माना जा सकता है। अब एकसमान च्बकीय क्षेत्र को धनात्मक :-दिशा में चालू करते हैं जिसका मान 0 से B तक एक सेकण्ड में एकसमान दर से बढ़ता है। यह मानिए कि इस दौरान कक्ष की त्रिज्या स्थिर रहती है। चुम्बकीय क्षेत्र के लगाने से कक्ष में एक emf प्रेरित होता है। एक प्रेरित विद्युत क्षेत्र द्वारा इकाई धन आवेश को संवृत्त लूप के चारों ओर घुमाने में किए गए कार्य की मात्रा को प्रेरित विद्युत वाहक बल (emf) कहा जाता है। यह ज्ञात है कि जब एक आवेश एक कक्ष में परिभ्रमण करता है तब उसका चुम्बकीय द्विध्रुव आघूर्ण उसके कोणीय संवेग के अनुपातिक होता है जिसका अनुपातिक स्थिरांक γ है।
Q चुम्बकीय क्षेत्र के परिवर्तन के दौरान कक्ष में किसी विशेष क्षण पर प्रेरित विद्युत क्षेत्र का मान है
View Solutionचित्र में दर्शाये गये, α त्रिज्या वाला वृत्तीय पाश (Loop) तथा दो समान्तर तार अंकित 1 तथा 2 सभी पृष्ठ के तल में हैं। दोनों तार वृत्तीय पाश के केन्द्र से d दूरी पर हैं। वृत्तीय पाश तथा दोनों तारों में एकसमान धारा | प्रवाहित है। ऊपर से देखने पर वृत्तीय पाश में धारा की दिशा वामावर्त है।
Q जब d≅a लेकिन तार पाश को स्पर्श नहीं कर रहे हैं तब वृत्तीय पाश के अक्ष पर ऊँचाई पर परिणामी चुम्बकीय क्षेत्र शून्य मिलने की स्थिति में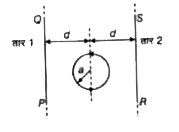
View Solutionएक स्थिर विद्युत धारा I समकोण त्रिभुजाकार लूप POR में प्रवाहित हो रही है। इस त्रिभुज की भुजाओं की लम्बाई, क्रमशः PQ = 3x, PR = 4x तथा QR = 5x है। बिन्दु P पर लूप से उत्पन्न चुम्बकीय क्षेत्र का मान k (μ0I48πx) है k का मान ज्ञात कीजिए।
View Solutionदो डिस्कें A तथा B एक ऊर्ध्वाधर धुरी पर समाक्ष रूप से अवस्थिरत की गई है। उभयनिष्ठ अक्ष के परितः उन चकतियों के जड़त्व आघूर्ण क्रमशः I तथा 2I है। एक स्पि्रंग को x1 दूरी से दबाकर उसकी सम्पूर्ण स्थितिज ऊर्जा का उपयोग करके, चकती A को प्रारंभिक कोणीय वेग 2ω दिया जाता है। उतने ही स्पि्रंग गुणांक वाले एक दूसरे स्पि्रंग को x2 दूरी से दबाकर डिस्क B को कोणीय वेग ω दिया जाता है। दोनों चकतियां दक्षिणावर्त दिशा में घूम रही हैं
अनुपात x1/x2 है।
View Solutionअधिकतर पदार्थो का अपवर्तनांक, n>1 होता है। इसलिये जब कोई प्रकाश किरण वायु से किसी प्राकृतिक पदार्थ में प्रवेश करती है तब, Snell's नियम, sinθ1sinθ2=n2n1के अनुसार, अपवर्तित किरण अभिलंब की तरफ झुकती है। लेकिन यह कभी भी अभिलंब के आपतित किरण वाले ओर से बाहर नहीं निकलती। विद्युत-चुम्बकत्व के अनुसार, किसी माध्यम का अपवर्तनांक n=(cv)=±√εrμr, होता है, जहाँ C विद्युत – चुम्बकीय तरंगों की निर्यात में चाल तथा v उनकी माध्यम में चाल हैं, εr व μr क्रमशः माध्यम की सापेक्ष विद्युतशीलता व चुंबकशीलता हैं। आम पदार्थों में εr व μr दोनों धनात्मक होते हैं, अर्थात माध्यम का n धनात्मक है। जब εr व μr दोनों ऋणात्मक हों तब हमें n का ऋणात्मक वर्गमूल लेना होगा। ऐसे ऋणात्मक n वाले पदार्थ अब अप्राकृतिक रूप में तैयार किये जा सकते हैं, और उन्हें मैटा-पदार्थ (meta-metarial) कहते हैं। वे बिलकुल अलग तरह का प्रकाशिक गुणधर्म दर्शाते हैं, परंतु भौतिक नियमों का उल्लंघन नहीं करते। चूँकि n ऋणात्मक है, अपवर्तित प्रकाश की चलने की दिशा में परिवर्तन होता है। तथापि आम पदार्थों की तरह इन मैटा-पदार्थों में भी अपवर्तन पर प्रकाश की आवृत्ति नहीं बदलती।
सही प्रकथन चुनें।
View Solutionएकसमान विद्युत क्षेत्र E=3×103ˆi(N)/C पर विचार कीजिये ।
(a) इस क्षेत्र का 10 cm भुजा के वर्ग के उस पार्श्व से जिसका तल yz तल के समांतर है, गुजरने वाला फ्लक्स क्या है ?
(b) इस वर्ग से गुजरने वाला फ्लक्स कितना है यदि इसके तल का अभिलंब x- अक्ष से 60∘ कोण बनता है ?
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionएक परवलय की नाभि मूलबिंदु पर है तथा रेखा x=2 परवलय की नियता है , तो परवलय का शीर्ष है
View Solutionएक परवलय के नाभिलम्ब का समीकरण x+y=8 तथा उसके शीर्ष पर स्पर्शी का समीकरण x+y=12 है, तो उसके नाभिलम्ब की लम्बाई है :
View Solutionयदि एक दीर्घवृत्त जिसका केंद्र मूलबिंदु पर है, के दीर्घ कक्ष तथा लघु कक्ष कि लम्बाइयों का अंतर 10 है तथा एक नाभिकेन्द्र (0,5√3) पर है, तो इसके नाभिलम्ब की लम्बाई है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionसरल रेखा x+2y=1 निर्देशांक अक्षों को A तथा B पर काटती है। मूलबिंदु , A तथा B से होकर जाने वाला वृत्त खींचा गया है , तो मूलबिंदु पर वृत्त की स्पर्श रेखा की A तथा B से लम्बवत दूरियों का योग है
View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
View Solution
