एक वलय जिसकी त्रिज्या R है, उस पर आवेश एकसमान रूप से वितरित है। यह वलय दो एक जैसी डोरियों द्वारा निलम्बित छड़ पर चढ़ा हुआ है। साम्यावस्था में डोरियों में तनाव T0 है। एक ऊर्ध्वाधर चुम्बकीय क्षेत्र को प्रारम्भ करने पर वलय कोणीय चाल ω से घूर्णन करने लगता है। यदि डोरियों के तनाव की अधिकतम सीमा 3T02 है तो ω का अधिकतम मान जिससे कि वलय घूम सके क्या होगा?
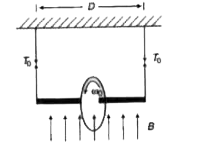
The correct Answer is:ωmax=DT0BQR2
साम्यावस्था में,
2T0 = mg
T0=mg2
चुम्बकीय आघूर्ण, M = iA= (ω2πQ)(πR2)
τ=MBsin90∘=ωBQR2
माना चुम्बकीय क्षेत्र को चालू कर देने पर दोनों डोरियों में तनाव क्रमश: T, RT2 (T. >T) हैं।
वलय के स्थानान्तरीय सन्तुलन के लिए,
T1+T2)=mg ....(ii)
घूर्णन सन्तुलन के लिए,
(T1+T2)D2=τ=ωBQR22
T1−T2=ωBQR22
समी (ii) व (iii) से
T1=mg2+ωBQR22D
चूँकि , T1>T2 तथा T1, का अधिकतम मान 3T02 है, तब
3T02=T0+omrgamaxBQR22D⟨.mg2=T0)
∴ωmax=DT0BQR2
Topper's Solved these Questions
- चुम्बकत्व BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - चुम्बकत्व EXERCISE - श्रृंखलाबद्ध-बोधन प्रकार (अनुच्छेद।)
2 Videos
- चुम्बकत्व BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - चुम्बकत्व EXERCISE - श्रृंखलाबद्ध-बोधन प्रकार (अनुच्छेद ii )
2 Videos
- चुम्बकत्व BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - चुम्बकत्व EXERCISE - एकल पूर्णांक उत्तर प्रकार
5 Videos
- घूर्णन गतिBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - घूर्णन गतिEXERCISE - श्रृंखलाबद्ध बोधन प्रकार
10 Videos
- तरंगे BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - तरंगे EXERCISE - श्रंखलाबद्ध - बोधन प्रकार (अनुच्छेद III )
2 Videos
Similar Questions
X-Y तल में R त्रिज्या की वृत्तीय कक्षा में एक बिन्दु आवेश ω कोणीय गति से परिक्रमा कर रहा है। इसे लूप में बहती हुई Qω2π अपरिवर्ती धारा के तुल्य माना जा सकता है। अब एकसमान च्बकीय क्षेत्र को धनात्मक :-दिशा में चालू करते हैं जिसका मान 0 से B तक एक सेकण्ड में एकसमान दर से बढ़ता है। यह मानिए कि इस दौरान कक्ष की त्रिज्या स्थिर रहती है। चुम्बकीय क्षेत्र के लगाने से कक्ष में एक emf प्रेरित होता है। एक प्रेरित विद्युत क्षेत्र द्वारा इकाई धन आवेश को संवृत्त लूप के चारों ओर घुमाने में किए गए कार्य की मात्रा को प्रेरित विद्युत वाहक बल (emf) कहा जाता है। यह ज्ञात है कि जब एक आवेश एक कक्ष में परिभ्रमण करता है तब उसका चुम्बकीय द्विध्रुव आघूर्ण उसके कोणीय संवेग के अनुपातिक होता है जिसका अनुपातिक स्थिरांक γ है।
Q चुम्बकीय क्षेत्र के परिवर्तन के दौरान कक्ष में किसी विशेष क्षण पर प्रेरित विद्युत क्षेत्र का मान है
View Solutionचित्र में दर्शाये गये, α त्रिज्या वाला वृत्तीय पाश (Loop) तथा दो समान्तर तार अंकित 1 तथा 2 सभी पृष्ठ के तल में हैं। दोनों तार वृत्तीय पाश के केन्द्र से d दूरी पर हैं। वृत्तीय पाश तथा दोनों तारों में एकसमान धारा | प्रवाहित है। ऊपर से देखने पर वृत्तीय पाश में धारा की दिशा वामावर्त है।
Q जब d≅a लेकिन तार पाश को स्पर्श नहीं कर रहे हैं तब वृत्तीय पाश के अक्ष पर ऊँचाई पर परिणामी चुम्बकीय क्षेत्र शून्य मिलने की स्थिति में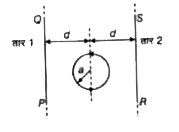
View Solutionएक स्थिर विद्युत धारा I समकोण त्रिभुजाकार लूप POR में प्रवाहित हो रही है। इस त्रिभुज की भुजाओं की लम्बाई, क्रमशः PQ = 3x, PR = 4x तथा QR = 5x है। बिन्दु P पर लूप से उत्पन्न चुम्बकीय क्षेत्र का मान k (μ0I48πx) है k का मान ज्ञात कीजिए।
View Solutionदो डिस्कें A तथा B एक ऊर्ध्वाधर धुरी पर समाक्ष रूप से अवस्थिरत की गई है। उभयनिष्ठ अक्ष के परितः उन चकतियों के जड़त्व आघूर्ण क्रमशः I तथा 2I है। एक स्पि्रंग को x1 दूरी से दबाकर उसकी सम्पूर्ण स्थितिज ऊर्जा का उपयोग करके, चकती A को प्रारंभिक कोणीय वेग 2ω दिया जाता है। उतने ही स्पि्रंग गुणांक वाले एक दूसरे स्पि्रंग को x2 दूरी से दबाकर डिस्क B को कोणीय वेग ω दिया जाता है। दोनों चकतियां दक्षिणावर्त दिशा में घूम रही हैं
अनुपात x1/x2 है।
View Solutionअधिकतर पदार्थो का अपवर्तनांक, n>1 होता है। इसलिये जब कोई प्रकाश किरण वायु से किसी प्राकृतिक पदार्थ में प्रवेश करती है तब, Snell's नियम, sinθ1sinθ2=n2n1के अनुसार, अपवर्तित किरण अभिलंब की तरफ झुकती है। लेकिन यह कभी भी अभिलंब के आपतित किरण वाले ओर से बाहर नहीं निकलती। विद्युत-चुम्बकत्व के अनुसार, किसी माध्यम का अपवर्तनांक n=(cv)=±√εrμr, होता है, जहाँ C विद्युत – चुम्बकीय तरंगों की निर्यात में चाल तथा v उनकी माध्यम में चाल हैं, εr व μr क्रमशः माध्यम की सापेक्ष विद्युतशीलता व चुंबकशीलता हैं। आम पदार्थों में εr व μr दोनों धनात्मक होते हैं, अर्थात माध्यम का n धनात्मक है। जब εr व μr दोनों ऋणात्मक हों तब हमें n का ऋणात्मक वर्गमूल लेना होगा। ऐसे ऋणात्मक n वाले पदार्थ अब अप्राकृतिक रूप में तैयार किये जा सकते हैं, और उन्हें मैटा-पदार्थ (meta-metarial) कहते हैं। वे बिलकुल अलग तरह का प्रकाशिक गुणधर्म दर्शाते हैं, परंतु भौतिक नियमों का उल्लंघन नहीं करते। चूँकि n ऋणात्मक है, अपवर्तित प्रकाश की चलने की दिशा में परिवर्तन होता है। तथापि आम पदार्थों की तरह इन मैटा-पदार्थों में भी अपवर्तन पर प्रकाश की आवृत्ति नहीं बदलती।
सही प्रकथन चुनें।
View Solutionसुसंगत क्षेत्र में बिंदु जो उदेश्य फलन का इष्टतम मान (अधिकतम या न्यूनतम ) एक देता है, वह कहलाता है -
View Solutionनिम्न कथन सत्य है अथवा असत्य-
उद्देश्य फलन का अधिकतम मान, परिबद्ध क्षेत्र के किसी एक शीर्ष पर होता है।
View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
View Solutionयदि एक दीर्घवृत्त जिसका केंद्र मूलबिंदु पर है, के दीर्घ कक्ष तथा लघु कक्ष कि लम्बाइयों का अंतर 10 है तथा एक नाभिकेन्द्र (0,5√3) पर है, तो इसके नाभिलम्ब की लम्बाई है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
View Solutionनिम्नलिखित कॉलम को सुमेलित कीजिये
कॉलम-I कॉलम-II(A) एक समान आवेशित परावैधुत वलय(p) निकाय के बाहर नियत स्थिर विधुत क्षेत्र है(B) एक सामान आवेशित परावैधुत वलय कोणीय वेग ωसे घूर्णित है (q)चुम्बकीय क्षेत्र की तीव्रता(C) वलय में नियत धारा i(r)वैधुत क्षेत्र (प्रेरित)(D)i=i0cosωt(s) चुम्बकीय द्वि - ध्रुव आघूर्ण
View Solution....... करने पर धातु का छड़ फैलता है।
View Solutionजब धातु M को NaOH के साथ उपचारित किया जाता है, तो एक श्वेत जिलेटिन जैसा अवक्षेप 'X' प्राप्त होता है, जो NaOH के आधिक्य में घुलनशील होता है। यौगिक 'X' प्रबल रूप से गर्म करने पर एक ऑक्साइड देता है जिसका उपयोग वर्णलेखिकी में एक अधिशोषक के रूप में किया जाता है। धातु 'M' है:
View Solutionएक ठोस यौगिक X को गर्म करने पर यह CO2 गैस और एक अवशिष्ट देता है। अवशिष्ट जल के साथ मिश्रित होकर Y बनाता है। जल में Y के माध्यम से CO2 आधिक्य को गुजारने पर एक स्वच्छ विलयन Z प्राप्त होता है। Z को उबलने पर, यौगिक X का पुनः निर्माण होता है। यौगिक X है
View Solution
