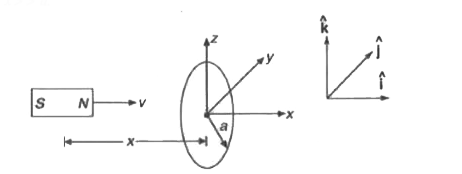
एक अनन्त सूक्ष्म दण्ड चुम्बक के द्विध्रुव आघूर्ण M तथा दण्ड चुम्बक के वेग दोनों दिशा धन x-दिशा में हैं। एक छोटा बन्द वृत्ताकार चालक लूप, जिसकी त्रिज्या a है तथा स्वप्रेरण (Self inductance) नगण्य है, -तल में स्थित है, इसका केन्द्र .x=0 पर है, तथा इसकी अक्ष :-अक्ष के संपाती है। यदि लूप का प्रतिरोध है, तो चुम्बक की गति का विरोधी बल ज्ञात कीजिए। यह मान लीजिए कि चुम्बक की लूप के केन्द्र से दूरी x, लूप की त्रिज्या a से बहुत बड़ी है
The correct Answer is:.F=214μ20M2a4VRX8(प्रतिकर्षण)
जबν=νT2=mgR2B2L2
a=g−(mgR2B2L2)(B2L2mR)=g−g2
या a=g/2xgtgta
छड़ चुम्बक के कारण कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र,
B=μ04π2Mx3
कुण्डली से बद्ध चुम्बकीय फ्लक्स,
ϕ=BS=μ02πMx3(πa3)=μ0Ma22x2
∴ प्रेरित वि० वा० बल
e=−dϕdt=−(μ0Ma22)ddt(1x3)
=μ0Ma22(3x4)dxdt32μ0Ma2x4ν
(∵dxdt=ν)
कुण्डली में प्रेरित धारा,i=eR=32μ0Ma2Rx4ν
प्रेरित धारा के कारण चुम्बकीय आघूर्ण,
M.=iS=32μ0Ma2Rx4ν(πa2)
m.=32μ0πMa4νRx(4)
M. की B में स्थितिज ऊर्जा, U=−M’Bcos180∘
U=M’B
∴U=32μ0πMa4νRx2(μ02π.Mx3)
thereforeF=−dUdx=214μ20M2a4νRx8 का धनात्मक चिन्ह यह बताता है कि चुम्बक व कुण्डली के बीच प्रतिकर्षण है।
Topper's Solved these Questions
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - विद्युतचुम्बकीय प्रेरण एंव प्रत्यावर्ती धाराEXERCISE - श्रृंखलाबद्ध-बोधन प्रकार (अनुच्छेद-1)3videos
विद्युतचुम्बकीय प्रेरण एंव प्रत्यावर्ती धारा
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - विद्युतचुम्बकीय प्रेरण एंव प्रत्यावर्ती धाराEXERCISE - श्रृंखलाबद्ध-बोधन प्रकार (अनुच्छेद-II)3videos
विद्युतचुम्बकीय प्रेरण एंव प्रत्यावर्ती धारा
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - विद्युतचुम्बकीय प्रेरण एंव प्रत्यावर्ती धाराEXERCISE - एकल पूर्णांक उत्तर प्रकार1videos
विद्युतचुम्बकीय प्रेरण एंव प्रत्यावर्ती धारा
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रयोगात्मक भौतिकी EXERCISE - बहुविकल्पीय प्रश्न II3videos
प्रयोगात्मक भौतिकी
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - विविध प्रश्नEXERCISE - श्रृंखलाबद्ध –बोधन प्रकार2videos
विविध प्रश्न
Similar Questions
C धारिता के संधारित्र को (एक . प्रतिरोध R की सहायता से) स्विच S1 को बन्द तथा स्विच S2 को खुला रखते हुए, V वोल्ट के स्रोत द्वारा आवेशित किया जाता है। स्विच, को खुला तथा S1, को बन्द रखकर संधारित्र के श्रेणी क्रम में एक प्रेरकत्व जोड़ा जाता है।
Q प्रारम्भ में संधारित्र अनावेशित था। अब स्विच S1, को बन्द तथा S2 को खुला रखा जाता है। यदि इस परिपथ का समय नियतांक τ है, तब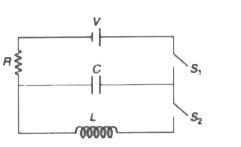
05:19View Solutionआधुनिक रेलगाड़ियाँ मैगलेव तकनीक (Maglev technology) पर आधारित हैं जिसमें गाड़ियाँ चुम्बकीय विधि से ऊपर उठी रहती हैं, जो EDS मैगलेव निकाय में दौड़ती हैं। पहियों के दोनों ओर कुण्डलियाँ रहती हैं। गाड़ी की गति के कारण, कुण्डलियों में प्रेरित धारा उत्पन्न हो जाती है, जो उसे ऊपर उठा देती है। यह क्रिया लेन्ज़ के नियमानुसार होती है। यदि गाड़ी नीचे आती है, तो लेन्ज के नियम के कारण एक प्रतिकर्षण बल बढ़ जाता है, जिससे गाड़ी ऊपर उठ जाती है तथा यदि यह अधिक ऊपर उठ जाती है तो यह प्रभावी अधोगामी बल के प्रभाव से गुरुत्व के अधीन नीचे आ जाती है।
मैगलेव गाड़ियों का लाभ यह है कि पथ व गाड़ियों के बीच घर्षण नहीं होता, जिससे ऊर्जा का उपभोग कम होता है तथा गाड़ियाँ अधिक वेग से गति कर सकती हैं। मैगलेव गाड़ियों की हानि यह है कि कोई गाड़ी धीमे हो जाती है तो विद्युतचुम्बकीय बल कम हो जाता है तथा तब इसे ऊपर उठाए रखने में कठिनाई होती है और जैसे-जैसे यह आगे बढ़ती है (लेन्ज के नियमानुसार) उस पर विद्युतचुम्बकीय शिथिल बल (Drag force) लगने लगता है
Qइस निकाय का क्या लाभ है03:29View Solutionदो प्रेरकों (Inductors) L1तथाL2का प्रेरकत्व क्रमश: 1 मिली हेनरी एवं 2 मिली हेनरी हैं, एवं आन्तरिक प्रतिरोध क्रमश: 3Ω एवं 4Ω हैं। इन दोनों प्रेरकों तथा एक प्रतिरोधक R, जिसका प्रतिरोष 12Ωहै, सभी को एक 5 वोल्ट की बैटरी से समान्तर क्रम में जोड़ दिया गया है। परिपथ को समय t=0 पर चालू किया जाता है। बैटरी से निकली अधिकतम एवं न्यूनतम धाराओं का अनुपातImaxImin क्या होगा
05:46View Solutionएक छात्र ने u-v विधि से अवतल दर्पण की फोकस दूरी निकालने का प्रयोग किया। प्रयोग में उपयोग किये गये अवतल दर्पण की फोकस दूरी 24 cm तथा प्रकाशीय बैच की लम्बाई 1.5 m थी। प्रतिबिम्ब की स्थिति के निर्धारण में हुई अधिकतम त्रुटि 0.2 cm हो सकती है। छात्र द्वारा लिखे गये (u.v) के पांच मान (cm में) इस प्रकार थे. (42.56). (48.48). (60, 40). (66.33). (78.39)। (u.v) के मान जो प्रयोग के द्वारा प्राप्त नही हो सकते और गलत लिखे गये, वह है (वे हैं)
04:42View Solutionकिसी पदार्थ का प्रतिरोध, जो कि अतिचालक है, इसका ताप क्रांतिक ताप TC(0) से कम करने पर अचानक अशून्य मान से शून्य तक परिवर्तित हो जाता है।
अतिचालक का एक रूचिकर गुण यह है कि यदि इन्हें चुम्बकीय क्षेत्र में रखा जाय तब, इनका क्रांतिक ताप TC(0) से घटने लगता है, अर्थात् क्रांतिक ताप TC(B), चुम्बकीय क्षेत्र की तीव्रता B का फलन होता है। TC(B) की B पर निर्भरता चित्र में प्रदर्शित है।
नीचे दिये गये ग्राफ में, दो भिन्न मान के चुम्बकीय क्षेत्रों B1 (सरल रेखा) तथा B2 (बिन्दुवत रेखा) के लिये अतिचालक के प्रतिरोध R को इसके ताप के फलन के रूप में दिखाया गया है। यदि B2 का मान B1 से बड़ा है तब इन चुम्बकीय क्षेत्रों में कौनसा ग्राफ R में T के साथ उचित परिवर्तन प्रदर्शित करता है03:33View Solutionसिद्ध कीजिए कि समीकरण y2+2ax+2by+c=0 एक परवलय निरूपित करती है जिसका अक्ष x-अक्ष के समान्तर है । इसका शीर्ष ज्ञात कीजिए ।
04:10View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
03:14View Solutionएक त्रिभुज , जिसके शीर्ष (0,0),(0,41) तथा (41,0) है , के आंतरिक भाग में स्थित उन बिंदुओं की संख्या जिनके दोनों निर्देशांक पूर्णांक है , है :
04:45View Solutionसिद्ध कीजिए कि y2+2ax+2by+c=0 एक परवलय को निरूपित करता है जिसका अक्ष x-अक्ष के समांतर है। इसका शीर्ष तथा इसके नाभिलम्ब का समीकरण ज्ञात कीजिए।
02:29View Solutionकोई रेखा x-अक्ष और y-से साथ क्रमशः 60∘ तथा 45∘ के कोण बनाती है। इनके द्वारा घनत्व दिशा में z-अक्ष के साथ कितना कोण बनेगा ?
03:50View Solutionएक बहुविकल्पीय प्रश्न का उत्तर देने में विद्यार्थी या तो प्रश्न का उत्तर जानता है या जानता लगाता है | मान ले कि उसके उत्तर जान ने कि प्रायिकता 35 है तथा अनुमान लगाने कि प्रायिकता 25 है | मान ले कि छात्र के प्रश्न का उत्तर अनुमान लगाने पर सही उत्तर देने कि प्रायिकता 13 है , तो इसकी क्या प्रायिकता है कि कोई छात्र प्रश्न का उत्तर जानता है यदि यह ज्ञात है कि उसने सही उत्तर दिया है ?
04:26View Solutionयदि एक दीर्घवृत्त जिसका केंद्र मूलबिंदु पर है, के दीर्घ कक्ष तथा लघु कक्ष कि लम्बाइयों का अंतर 10 है तथा एक नाभिकेन्द्र (0,5√3) पर है, तो इसके नाभिलम्ब की लम्बाई है
05:19View Solutionएक परवलय का अक्ष X-अक्ष के अनुदिश है। यदि इसके शीर्ष तथा नाम नाभि , X-अक्ष कि धनात्मक दिशा में मूलबिंदु से क्रमशः 2 तथा 4 कि दुरी पर हैं , तो इनमें से कौन - सा बिन्दु इस परवलय पर स्थित नहीं है ?
04:06View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
04:29View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
04:37View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
05:59View Solution