एक थर्मोकोल से बने बर्तन में 0.5 किग्रा आसुत जल 30∘C पर भरा है। धातु की एक कुण्डली, जिसका क्षेत्रफल 5×10−3मी2', फेरों की संख्या 100, द्रव्यमान 0.06 किग्ना तथा प्रतिरोध 1.6Ω है, बर्तन की तली पर क्षैतिज रखी है। समय t=0 पर एकसमान समय-परिवर्ती चुम्बकीय क्षेत्र कुण्डली में से ऊर्ध्वतः गुजरते हुए लगाया जाता है। क्षेत्र पहले 0 तथा 0.2 सेकण्ड के बीच एक नियत दर से शून्य से 0.8 टेसला तक बढ़ाया जाता है, तथा फिर उसी दर से 0.2 तथा 0.4 सेकण्ड के बीच शून्य तक घटाया जाता है। यह चक्र 12000 बार दोहराया जाता है। पहले दो चक्रों के लिए कुण्डली में प्रवाहित धारा तथा कुण्डली में क्षय शक्ति का समय के साथ फलन (Function) का आरेख खींचिए। अक्षों पर राशियों के परिमाण स्पष्ट रूप से दिखाइए। यह मान लीजिए कि बर्तन तथा परिवेश से ऊष्मा की कोई हानि नहीं होती है। ऊष्मीय साम्यावस्था में जल का अन्तिम ताप ज्ञात कीजिए। धातु की विशिष्ट ऊष्मा = 500 जूल किग्रा−1K−1 तथा जल की विशिष्ट ऊष्मा = 4200 जूल किग्रा−1 K(−1)' है। कुण्डली के प्रेरकत्व को छोड़ा जा सकता है
समय t के साथ चुम्बकीय क्षेत्र B का परिवर्तन चित्र में प्रदर्शित है|
dBdt∣=0.80.2=4टेसला से−1
कुण्डली से गुजरने वाले चुम्बकीय फ्लक्स में परिवर्तन के कारण प्रेरित वि० वा० बल,e=∣∣∣dϕdt∣∣∣=NA∣∣∣dBdt∣∣∣
यहाँ, A = कुण्डली का क्षेत्रफल =5×10−3मी2
N= फेरों की संख्या = 100
∴e=(100)(5×10−3)(4)=2वोल्ट
कुण्डली में धारा, i=eR=21.6=1.25ऐम्पियर 0 से 0.2 सेकण्ड तक तथा 0.4 से 0.6 सेकण्ड तक कुण्डली में चुम्बकीय क्षेत्र का मान बढ़ता है, जबकि 0.2 से 0.4 सेकण्ड तक तथा 0.6 सेकण्ड से 0.8 सेकण्ड तक कुण्डली में चुम्बकीय क्षेत्र का मान घटता है। अत: इन दोनों समयान्तरालों में कुण्डली से जाने वाली धाराएँ एक-दूसरे के विपरीत होंगी। इस आधार पर कुण्डली में धारा (i) व समय (t) में ग्राफीय निरूपण निम्न प्रकार होगा।
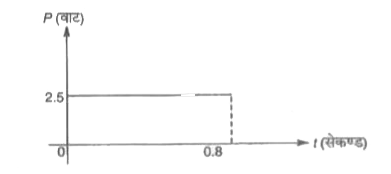
कुण्डली में शक्ति क्षय, P=i2R=(1.25)2(1.6)=2.5वाट
शक्ति, कुण्डली में धारा की दिशा से स्वतन्त्र है। अत: पहले दो चक्रों के लिए शक्ति (P) तथा समय (t) के बीच वक्र निम्न प्रकार होगा
12000 चक्रों में कुल उत्पन्न ऊष्मा, H=P.t=(2.5)(12000)(0.4) यह ऊष्मा कुण्डली तथा जल का ताप बढ़ाने में प्रयुक्त होती है। माना अन्तिम ताप θ है, तब H=mwSw(θ−30)+mcSc(θ−30)
∴12000=(0.5)(4200)(θ−30)+(0.06)(500)(θ−30)
याθ=35.6∘C
Topper's Solved these Questions
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - विद्युतचुम्बकीय प्रेरण एंव प्रत्यावर्ती धाराEXERCISE - श्रृंखलाबद्ध-बोधन प्रकार (अनुच्छेद-1)3videos
विद्युतचुम्बकीय प्रेरण एंव प्रत्यावर्ती धारा
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - विद्युतचुम्बकीय प्रेरण एंव प्रत्यावर्ती धाराEXERCISE - श्रृंखलाबद्ध-बोधन प्रकार (अनुच्छेद-II)3videos
विद्युतचुम्बकीय प्रेरण एंव प्रत्यावर्ती धारा
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - विद्युतचुम्बकीय प्रेरण एंव प्रत्यावर्ती धाराEXERCISE - एकल पूर्णांक उत्तर प्रकार1videos
विद्युतचुम्बकीय प्रेरण एंव प्रत्यावर्ती धारा
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रयोगात्मक भौतिकी EXERCISE - बहुविकल्पीय प्रश्न II3videos
प्रयोगात्मक भौतिकी
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - विविध प्रश्नEXERCISE - श्रृंखलाबद्ध –बोधन प्रकार2videos
विविध प्रश्न
Similar Questions
C धारिता के संधारित्र को (एक . प्रतिरोध R की सहायता से) स्विच S1 को बन्द तथा स्विच S2 को खुला रखते हुए, V वोल्ट के स्रोत द्वारा आवेशित किया जाता है। स्विच, को खुला तथा S1, को बन्द रखकर संधारित्र के श्रेणी क्रम में एक प्रेरकत्व जोड़ा जाता है।
Q प्रारम्भ में संधारित्र अनावेशित था। अब स्विच S1, को बन्द तथा S2 को खुला रखा जाता है। यदि इस परिपथ का समय नियतांक τ है, तब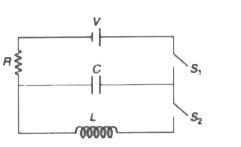
02:05View Solutionआधुनिक रेलगाड़ियाँ मैगलेव तकनीक (Maglev technology) पर आधारित हैं जिसमें गाड़ियाँ चुम्बकीय विधि से ऊपर उठी रहती हैं, जो EDS मैगलेव निकाय में दौड़ती हैं। पहियों के दोनों ओर कुण्डलियाँ रहती हैं। गाड़ी की गति के कारण, कुण्डलियों में प्रेरित धारा उत्पन्न हो जाती है, जो उसे ऊपर उठा देती है। यह क्रिया लेन्ज़ के नियमानुसार होती है। यदि गाड़ी नीचे आती है, तो लेन्ज के नियम के कारण एक प्रतिकर्षण बल बढ़ जाता है, जिससे गाड़ी ऊपर उठ जाती है तथा यदि यह अधिक ऊपर उठ जाती है तो यह प्रभावी अधोगामी बल के प्रभाव से गुरुत्व के अधीन नीचे आ जाती है।
मैगलेव गाड़ियों का लाभ यह है कि पथ व गाड़ियों के बीच घर्षण नहीं होता, जिससे ऊर्जा का उपभोग कम होता है तथा गाड़ियाँ अधिक वेग से गति कर सकती हैं। मैगलेव गाड़ियों की हानि यह है कि कोई गाड़ी धीमे हो जाती है तो विद्युतचुम्बकीय बल कम हो जाता है तथा तब इसे ऊपर उठाए रखने में कठिनाई होती है और जैसे-जैसे यह आगे बढ़ती है (लेन्ज के नियमानुसार) उस पर विद्युतचुम्बकीय शिथिल बल (Drag force) लगने लगता है
Qइस निकाय का क्या लाभ है05:07View Solutionदो प्रेरकों (Inductors) L1तथाL2का प्रेरकत्व क्रमश: 1 मिली हेनरी एवं 2 मिली हेनरी हैं, एवं आन्तरिक प्रतिरोध क्रमश: 3Ω एवं 4Ω हैं। इन दोनों प्रेरकों तथा एक प्रतिरोधक R, जिसका प्रतिरोष 12Ωहै, सभी को एक 5 वोल्ट की बैटरी से समान्तर क्रम में जोड़ दिया गया है। परिपथ को समय t=0 पर चालू किया जाता है। बैटरी से निकली अधिकतम एवं न्यूनतम धाराओं का अनुपातImaxImin क्या होगा
04:14View Solutionएक छात्र ने u-v विधि से अवतल दर्पण की फोकस दूरी निकालने का प्रयोग किया। प्रयोग में उपयोग किये गये अवतल दर्पण की फोकस दूरी 24 cm तथा प्रकाशीय बैच की लम्बाई 1.5 m थी। प्रतिबिम्ब की स्थिति के निर्धारण में हुई अधिकतम त्रुटि 0.2 cm हो सकती है। छात्र द्वारा लिखे गये (u.v) के पांच मान (cm में) इस प्रकार थे. (42.56). (48.48). (60, 40). (66.33). (78.39)। (u.v) के मान जो प्रयोग के द्वारा प्राप्त नही हो सकते और गलत लिखे गये, वह है (वे हैं)
04:26View Solutionकिसी पदार्थ का प्रतिरोध, जो कि अतिचालक है, इसका ताप क्रांतिक ताप TC(0) से कम करने पर अचानक अशून्य मान से शून्य तक परिवर्तित हो जाता है।
अतिचालक का एक रूचिकर गुण यह है कि यदि इन्हें चुम्बकीय क्षेत्र में रखा जाय तब, इनका क्रांतिक ताप TC(0) से घटने लगता है, अर्थात् क्रांतिक ताप TC(B), चुम्बकीय क्षेत्र की तीव्रता B का फलन होता है। TC(B) की B पर निर्भरता चित्र में प्रदर्शित है।
नीचे दिये गये ग्राफ में, दो भिन्न मान के चुम्बकीय क्षेत्रों B1 (सरल रेखा) तथा B2 (बिन्दुवत रेखा) के लिये अतिचालक के प्रतिरोध R को इसके ताप के फलन के रूप में दिखाया गया है। यदि B2 का मान B1 से बड़ा है तब इन चुम्बकीय क्षेत्रों में कौनसा ग्राफ R में T के साथ उचित परिवर्तन प्रदर्शित करता है04:29View Solutionएक कण y=x2+2x से साथ-साथ चलता है। व्रक के किस बिंदु पर x तथा y निर्देशांक समान दर से परिवर्तित हो रहे है ?
05:40View Solutionएक ही कोटि की दो वर्ग आव्यूहों A तथा B पर विचार कीजिये। निम्न में से कौन-सा कथन सत्य है-
02:42View Solutionरेखा 4x−3y+2=0 के समांतर रेखाएं खींची गई है जो मूलबिंदु 35 से की दुरी पर है, तो निम्न में से कौन-सा एक बिंदु इनमे से किसी रेखा पर स्थित है?
02:26View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि एक अतिपरवलय के शीर्ष (−2,0) तथा (2,0) पर है तथा इसकी एक नाभि (−3,0) पर है, तो निम्न में से कौन-सा बिन्दु इस अतिपरवलय पर स्थित नहीं है
01:57View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
03:25View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
01:47View Solutionएक समबाहु त्रिभुज की भुजाएँ 2 सेमी/से की दर से बढ़ रही है। क्षेत्रफल के बढ़ने की दर, जबकि भुजा 10 सेमी हो, है
03:02View Solutionकॉलम - I में कुछ निश्चित स्थितियां दी गई है जिनमे प्रतिरोध का सीधा धात्विक तार प्रयुक्त किया है तथा कॉलम - II में कुछ परिणामी प्रभाव दिए है कॉलम - I के कथनो को कॉलम - II के कथनो से सुलमित कीजिए
कॉलम - I कॉलम - II(A)एक आवेशित संधारित्र को तार के सिरों से जोड़ा गया है(p) एक नियत धारा तार में से प्रवाहित होती है(B)तार को इसकी लम्बाई के लम्बवत नियत वेग से एक समान चुम्बकीय क्षेत्र में गतिमान किया जाता है चुम्बकीय क्षेत्र गति के तल के लम्बवत है(q)उष्मीय ऊर्जा तार में उत्पन्न होती है(C)तार को नियत विधुत क्षेत्र में रखा जाता है जिसकी दिशा तार की लम्बाई के अनुदिश है(r)तार के सिरों पर एक नियत विभवान्तर उत्पन्न होता है(D)तार के सिरों पर एक नियत वि. वा. बल. की बैट्री जोड़ी जाती है(s)तार के सिरों का नियत परिमाण का आवेश उपस्थित होता हैView Solution30 बच्चो की एक कक्षा में सरन शीर्ष से 9 वे रैंक पर है| मनीष सरन से पांच रैंक निचे है| तल से मनीष की रैंक क्या है?
View Solutionएक वस्तु पूर्व दिशा की ओर 30 मी/से के वेग से जा रही है। 10 सेकण्ड के बाद यह वस्तु 40 मी/से के वेग से उत्तर की ओर गति करती है। वस्तु का औसत त्वरण है-
View Solution