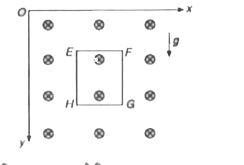
एक चुम्बकीय क्षेत्र B=(B0y/a)ˆk कागज के तल के लम्बवत् नीचे की ओर +z दिशा में है। B, Ra धन नियतांक हैं। एक वर्गाकार लूप EFGH जिसकी भुजा a, द्रव्यमान m तथा प्रतिरोध R है, X-y तल में गुरुत्व के अन्तर्गत गिरना प्रारम्भ करता है। चित्र में x तथा y-अक्षों की दिशाओं का ध्यान रखते हुए ज्ञात कीजिए।
(a) लूप में प्रेरित धारा तथा इसकी दिशा
(b) लूप पर कार्य करने वाला लॉरेन्ज बल तथा उसकी दिशा,
(c) लूप की चाल v(t) का व्यंजक तथा चाल का सीमान्त मान
The correct Answer is:35.6∘C
जब भुजा EF.,x−अक्ष से y दूरी पर है, तब लूप से गुजरने वाला चुम्बकीय फ्लक्स,
ϕ=∫dϕ=y+a∫(Y)B0yaady
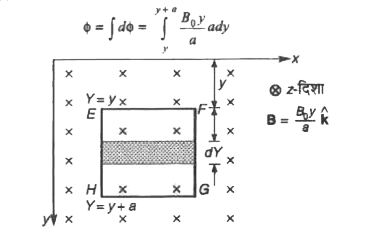
याϕ=B02[(y+a)2−y2]
प्रेरित वि० वा० बल,e=∣∣∣−dϕdt∣∣∣=∣∣∣−B02[2(y+a)−2y]dydt∣∣∣
e=B0adydt=B0νa
ν=dydt=लूपकीचाल
∴ प्रेरित धारा, i=eR=B0aνR
दिशा |B∝y अर्थात् जैसे-जैसे लूप नीचे आता है, तो लूप से जाने वाला चुम्बकीय क्षेत्र बढ़ता है, अत: प्रेरित धारा के कारण ⊙चुम्बकीय क्षेत्र या प्रेरित धारा लूप में दिशा वामावर्त होगी।
वैकल्पिक हल (a) EH तथा FG में गतिमान वि० वा० बल = 0 चूंकि v||I
EF में वि० वा० बल, e1=(B0ya)(a)ν=B0yν
[e/Blnu]
इसी प्रकार GH के लिए, e2={B0y+aa}(a)(ν)
=B0(a+y)ν
e1व e2की ध्रुवणताएँ चित्रानुसार होंगी।
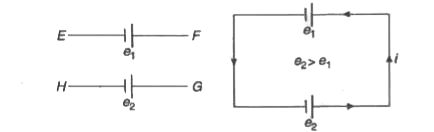
नेट वि० वा० बल, e=e2−e1
e=B0aν
∴i=eR=B0aνR(धारा की दिशा वामावर्त होगी)
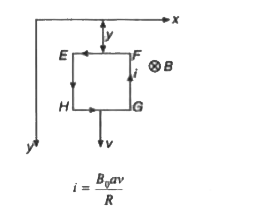
i=B0aνR
EH तथा FG पर चुम्बकीय बल बराबर परन्तु विपरीत होगे, अतः वे एक-दूसरे को निरस्त कर देंगे तथा लूप पर कोई बल कार्य नहीं करेगा।
FEf=(B0aνR)(a)(B0ya)(अधोगामी) (F=ilB)
=B20aνyR
तथाFGH=(B0aνR)(a)(B0(y+a)a)
=(B20aqνR)(y+a) (ऊर्ध्वगामी)
∴FGH>FEF
∴नेट लॉरेन्ज बल =FGH−FEF=B20a2νR (ऊर्ध्वगामी)F=−B20a2νRˆj
(c) लूप पर नेट बल, F = भार - (लॉरेन्ज बल)याF=mg−B20a2νR
याm(dνdt)=mg−(B20a2R)ν
∴dνdt=g−(B20a2mR)ν=g−kν
जहाँ, K=B20a2mR=नियतांक याdνg−Kν=dt
या∫ν0dνg−Kν=∫t0dt⇒ν=gK(1−e−kt
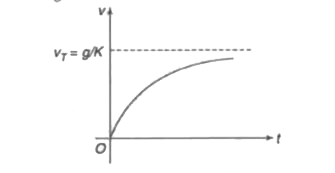
अर्थात् समय । के साथ लूप की चाल चरघातांकीय रूप में बढ़ रही है।
सीमान्त वेग,νT=gK=(mgRB20a2),o∞पर
Topper's Solved these Questions
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - विद्युतचुम्बकीय प्रेरण एंव प्रत्यावर्ती धाराEXERCISE - श्रृंखलाबद्ध-बोधन प्रकार (अनुच्छेद-1)3videos
विद्युतचुम्बकीय प्रेरण एंव प्रत्यावर्ती धारा
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - विद्युतचुम्बकीय प्रेरण एंव प्रत्यावर्ती धाराEXERCISE - श्रृंखलाबद्ध-बोधन प्रकार (अनुच्छेद-II)3videos
विद्युतचुम्बकीय प्रेरण एंव प्रत्यावर्ती धारा
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - विद्युतचुम्बकीय प्रेरण एंव प्रत्यावर्ती धाराEXERCISE - एकल पूर्णांक उत्तर प्रकार1videos
विद्युतचुम्बकीय प्रेरण एंव प्रत्यावर्ती धारा
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रयोगात्मक भौतिकी EXERCISE - बहुविकल्पीय प्रश्न II3videos
प्रयोगात्मक भौतिकी
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - विविध प्रश्नEXERCISE - श्रृंखलाबद्ध –बोधन प्रकार2videos
विविध प्रश्न
Similar Questions
C धारिता के संधारित्र को (एक . प्रतिरोध R की सहायता से) स्विच S1 को बन्द तथा स्विच S2 को खुला रखते हुए, V वोल्ट के स्रोत द्वारा आवेशित किया जाता है। स्विच, को खुला तथा S1, को बन्द रखकर संधारित्र के श्रेणी क्रम में एक प्रेरकत्व जोड़ा जाता है।
Q प्रारम्भ में संधारित्र अनावेशित था। अब स्विच S1, को बन्द तथा S2 को खुला रखा जाता है। यदि इस परिपथ का समय नियतांक τ है, तब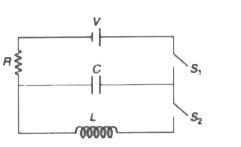 10:31View Solution
10:31View Solutionआधुनिक रेलगाड़ियाँ मैगलेव तकनीक (Maglev technology) पर आधारित हैं जिसमें गाड़ियाँ चुम्बकीय विधि से ऊपर उठी रहती हैं, जो EDS मैगलेव निकाय में दौड़ती हैं। पहियों के दोनों ओर कुण्डलियाँ रहती हैं। गाड़ी की गति के कारण, कुण्डलियों में प्रेरित धारा उत्पन्न हो जाती है, जो उसे ऊपर उठा देती है। यह क्रिया लेन्ज़ के नियमानुसार होती है। यदि गाड़ी नीचे आती है, तो लेन्ज के नियम के कारण एक प्रतिकर्षण बल बढ़ जाता है, जिससे गाड़ी ऊपर उठ जाती है तथा यदि यह अधिक ऊपर उठ जाती है तो यह प्रभावी अधोगामी बल के प्रभाव से गुरुत्व के अधीन नीचे आ जाती है।
मैगलेव गाड़ियों का लाभ यह है कि पथ व गाड़ियों के बीच घर्षण नहीं होता, जिससे ऊर्जा का उपभोग कम होता है तथा गाड़ियाँ अधिक वेग से गति कर सकती हैं। मैगलेव गाड़ियों की हानि यह है कि कोई गाड़ी धीमे हो जाती है तो विद्युतचुम्बकीय बल कम हो जाता है तथा तब इसे ऊपर उठाए रखने में कठिनाई होती है और जैसे-जैसे यह आगे बढ़ती है (लेन्ज के नियमानुसार) उस पर विद्युतचुम्बकीय शिथिल बल (Drag force) लगने लगता है
Qइस निकाय का क्या लाभ है08:27View Solutionदो प्रेरकों (Inductors) L1तथाL2का प्रेरकत्व क्रमश: 1 मिली हेनरी एवं 2 मिली हेनरी हैं, एवं आन्तरिक प्रतिरोध क्रमश: 3Ω एवं 4Ω हैं। इन दोनों प्रेरकों तथा एक प्रतिरोधक R, जिसका प्रतिरोष 12Ωहै, सभी को एक 5 वोल्ट की बैटरी से समान्तर क्रम में जोड़ दिया गया है। परिपथ को समय t=0 पर चालू किया जाता है। बैटरी से निकली अधिकतम एवं न्यूनतम धाराओं का अनुपातImaxImin क्या होगा
 08:27View Solution
08:27View Solutionएक छात्र ने u-v विधि से अवतल दर्पण की फोकस दूरी निकालने का प्रयोग किया। प्रयोग में उपयोग किये गये अवतल दर्पण की फोकस दूरी 24 cm तथा प्रकाशीय बैच की लम्बाई 1.5 m थी। प्रतिबिम्ब की स्थिति के निर्धारण में हुई अधिकतम त्रुटि 0.2 cm हो सकती है। छात्र द्वारा लिखे गये (u.v) के पांच मान (cm में) इस प्रकार थे. (42.56). (48.48). (60, 40). (66.33). (78.39)। (u.v) के मान जो प्रयोग के द्वारा प्राप्त नही हो सकते और गलत लिखे गये, वह है (वे हैं)
08:27View Solutionकिसी पदार्थ का प्रतिरोध, जो कि अतिचालक है, इसका ताप क्रांतिक ताप TC(0) से कम करने पर अचानक अशून्य मान से शून्य तक परिवर्तित हो जाता है।
अतिचालक का एक रूचिकर गुण यह है कि यदि इन्हें चुम्बकीय क्षेत्र में रखा जाय तब, इनका क्रांतिक ताप TC(0) से घटने लगता है, अर्थात् क्रांतिक ताप TC(B), चुम्बकीय क्षेत्र की तीव्रता B का फलन होता है। TC(B) की B पर निर्भरता चित्र में प्रदर्शित है।

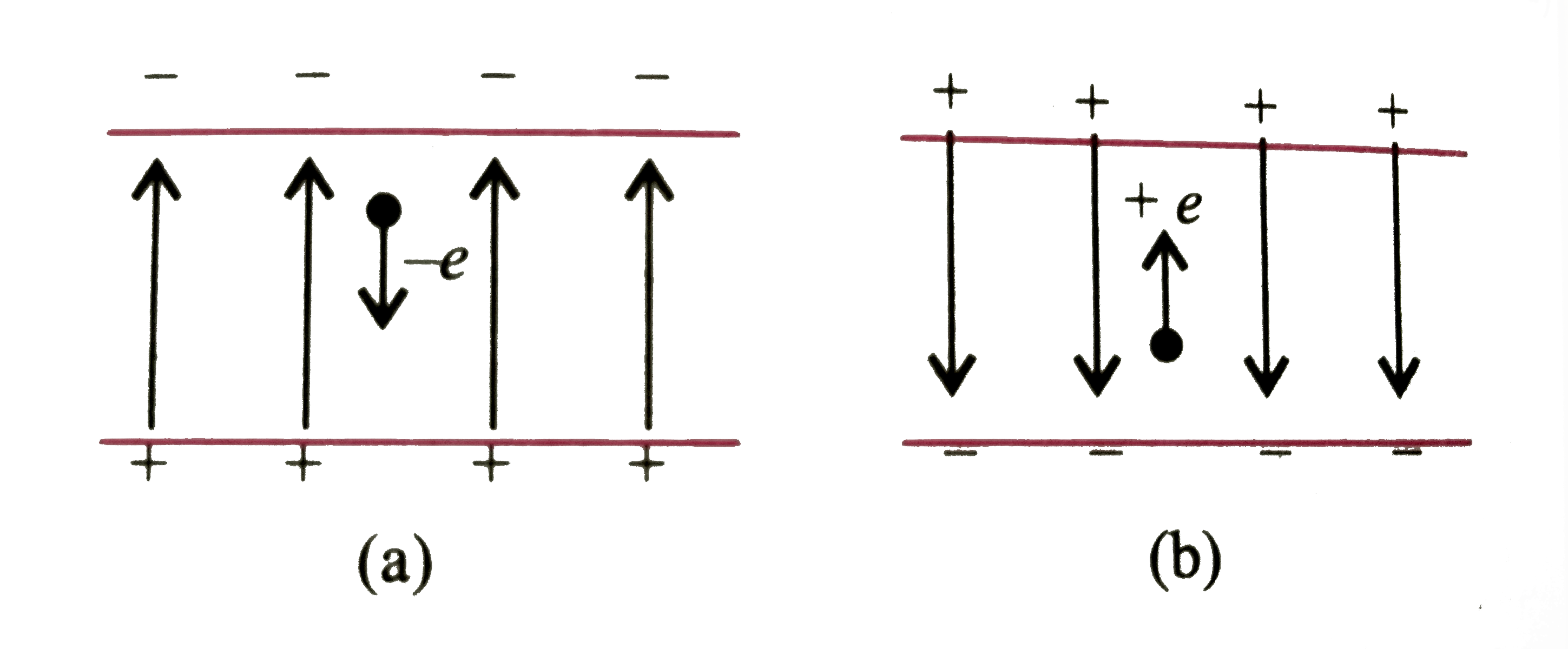
नीचे दिये गये ग्राफ में, दो भिन्न मान के चुम्बकीय क्षेत्रों B1 (सरल रेखा) तथा B2 (बिन्दुवत रेखा) के लिये अतिचालक के प्रतिरोध R को इसके ताप के फलन के रूप में दिखाया गया है। यदि B2 का मान B1 से बड़ा है तब इन चुम्बकीय क्षेत्रों में कौनसा ग्राफ R में T के साथ उचित परिवर्तन प्रदर्शित करता हैView Solutionकोई इलेक्ट्रॉन E=2.0×104 न्यूटन/कुलॉम परिणाम के एकसमान विद्युत क्षेत्र 1.5 से. मी. दुरी तक गिरता है। [चित्र (a )] क्षेत्र का परिणाम समान रखते हुए इनकी दिशा उत्क्रमित कर दी जाती है तथा अब कोई प्रोटॉन इस क्षेत्र में उतनी ही दुरी तक गिरता है [चित्र (b )] दोनों प्रकरणों में गिरने में लगे समय की गणना कीजिए । इस परिस्थिति का 'गुरुत्व के अधीन मुक्त पतन ' से तुलना कीजिए ।
 07:31View Solution
07:31View Solutionएक कम्पनी दो प्रकार के टेलीफोन A व B बनाती है | A प्रकार के टेलीफ़ोन बनाने में 2 घंटे एवं B प्रकार के टेलीफ़ोन बनाने में 4 घंटे लगते हैं |कम्पनी के पास 800 घंटे कार्य उपलब्ध है| 300 टेलीफोनों को एक दिन में पैक किया जाता है | A प्रकार के टेलीफोन का विक्रय मूल्य ₹300 तथा B प्रकार के टेलीफ़ोन का विक्रय मूल्य ₹400 है | अधिकतम लाभ के लिए कम्पनी A प्रकार के x तथा B प्रकार के y टेलीफोन का निर्माण करती है तो रेखीय प्रतिबंध के (x≥0,y≥0 अलावा ) है :
उपयुक्त प्रश्न के रेखीय कार्य योजना का सम्भाव्य क्षेत्र के निम्न प्रकार का है:02:33View Solutionएक कम्पनी दो प्रकार के टेलीफोन A व B बनाती है | A प्रकार के टेलीफ़ोन बनाने में 2 घंटे एवं B प्रकार के टेलीफ़ोन बनाने में 4 घंटे लगते हैं |कम्पनी के पास 800 घंटे कार्य उपलब्ध है| 300 टेलीफोनों को एक दिन में पैक किया जाता है | A प्रकार के टेलीफोन का विक्रय मूल्य ₹300 तथा B प्रकार के टेलीफ़ोन का विक्रय मूल्य ₹400 है | अधिकतम लाभ के लिए कम्पनी A प्रकार के x तथा B प्रकार के y टेलीफोन का निर्माण करती है तो रेखीय प्रतिबंध के (x≥0,y≥0 अलावा ) है :
उपयुक्त क्षेत्र के शीर्ष है:03:43View Solutionएक कम्पनी दो प्रकार के टेलीफोन A व B बनाती है | A प्रकार के टेलीफ़ोन बनाने में 2 घंटे एवं B प्रकार के टेलीफ़ोन बनाने में 4 घंटे लगते हैं |कम्पनी के पास 800 घंटे कार्य उपलब्ध है| 300 टेलीफोनों को एक दिन में पैक किया जाता है | A प्रकार के टेलीफोन का विक्रय मूल्य ₹300 तथा B प्रकार के टेलीफ़ोन का विक्रय मूल्य ₹400 है | अधिकतम लाभ के लिए कम्पनी A प्रकार के x तथा B प्रकार के y टेलीफोन का निर्माण करती है तो रेखीय प्रतिबंध के (x≥0,y≥0 अलावा ) है :
उपयुक्त प्रश्न का अनुकूलतम है निम्नलिखित शीर्ष पर है|View Solutionकॉलम - I में कुछ निश्चित स्थितियां दी गई है जिनमे प्रतिरोध का सीधा धात्विक तार प्रयुक्त किया है तथा कॉलम - II में कुछ परिणामी प्रभाव दिए है कॉलम - I के कथनो को कॉलम - II के कथनो से सुलमित कीजिए
कॉलम - I कॉलम - II(A)एक आवेशित संधारित्र को तार के सिरों से जोड़ा गया है(p) एक नियत धारा तार में से प्रवाहित होती है(B)तार को इसकी लम्बाई के लम्बवत नियत वेग से एक समान चुम्बकीय क्षेत्र में गतिमान किया जाता है चुम्बकीय क्षेत्र गति के तल के लम्बवत है(q)उष्मीय ऊर्जा तार में उत्पन्न होती है(C)तार को नियत विधुत क्षेत्र में रखा जाता है जिसकी दिशा तार की लम्बाई के अनुदिश है(r)तार के सिरों पर एक नियत विभवान्तर उत्पन्न होता है(D)तार के सिरों पर एक नियत वि. वा. बल. की बैट्री जोड़ी जाती है(s)तार के सिरों का नियत परिमाण का आवेश उपस्थित होता है49:27View SolutionAmpere has given a theory to find the magnetic field due to current distribution. in loop धारा I_(3) के चुम्बकीय क्षेत्र में अंशदान को नहीं लेते है क्योंकि चुम्बकीय क्षेत्र पुरे लूप मे युग्मित है। एक समाक्षीय केबिल में तार की त्रिज्या a है , इसके चारो ओर के बेलनाकार सेल की आंतरिक व बाह्य त्रिज्याएँ क्रमशः b तथा c है। अंदर वाले तार में i ऐम्पियर धारा बहती है तथा बाहरी सेल में बराबर व विपरीत धारा बहती है। अक्ष से x दूरी ( x lt a) पर चुंबकीय क्षेत्र है
View Solutionएक बस 3 घण्टे में 126 किमीo तथा एक ट्रेन 5 घण्टे में 315km दूरी तय करते है। बस तथा ट्रेन की चालों का अनुपात ज्ञात करो।
View Solutionएक व्यक्ति पश्चिम दिशा की ओर मूँह करके खड़ा है | वह दक्षिणावर्त दिशा में 45∘ के कोण पर घूमता है फिर वह पुनः उसी दिशा में 180∘ के कोण पर घूमता है और फिर वह वामावर्त दिशा में 270∘ के कोण पर घूमता है | अब वह किस दिशा की ओर खड़ा है ?
View Solutionयदि P, Q के उत्तर दिशा में तथा R,P के दक्षिण-पश्चिम में तथा S, Q के उत्तर-पूर्व में है, तो इनमे से कौन-सा निश्चित रूप से सत्य है?
View SolutionRecap|धारा लूप चुम्बकीय द्विध्रुव के रूप में |परिभ्रमण करते इलेक्ट्रॉन का चुम्बकीय द्विध्रुव आघूर्ण |OMR|Summary
View Solutionचित्र में दर्शाये अनुसार एक आदर्श गैस के एक मोल को A→B अनुसार लिया गया है। प्रक्रम में निहित कार्य का परिमाण है: (R=253JmolK)
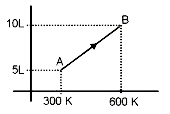 View Solution
View Solution

