लेंस मेकर सूत्र 1f=(n−1)(1R1−1R2) व्युत्पन्न कीजिए। किसी अवतल दर्पण का निचला आधार परावर्तक तल किसी अपारदर्शी पदार्थ से ढक दें तो दर्पण द्वारा बने प्रतिबिम्ब पर क्या प्रभाव पड़ेगा ?
लेंस मेकर सूत्र - एक पतला लेन्स L वायु में रखा हुआ है वायु के सापेक्ष लेन्स के पदार्थ का अपवर्तनांक n है और इसके पहले और दूसरे पृष्ठों की वक्रता त्रिज्यायें क्रमशः R1 तथा R2 है माना लेन्स की मोटाई t है।
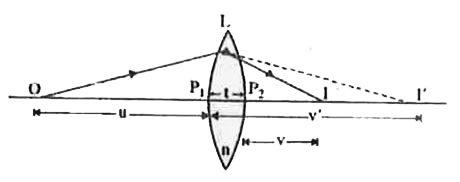
लेन्स के मुख्य अक्ष पर उसके प्रथम पृष्ठ के ध्रुव P1 से u दूरी पर एक बिन्दुवत वस्तु O रखी हुई है प्रथम पृष्ठ पर अपवर्तन से वस्तु O का प्रतिबिम्ब I. पर बनता है। माना कि I. की पृष्ठ के ध्रुव P1 से दूरी v. है | तब एकल गोलीय पृष्ठ पर अपवर्तन के सूत्र के अनुसार,
nv.−1n=n−1R1 . . . (1)
इस प्रकार बना हुआ प्रतिबिम्ब लेन्स के द्वितीय पृष्ठ के लिए जिसकी वक्रता त्रिज्या R2 है वस्तु का कार्य करेगा I. का प्रतिबिम्ब I अपने से v दूरी पर बनाता है
इस प्रकाश से सम्पूर्ण लेन्स द्वारा O का अंतिम प्रतिबिम्ब I पर बनता है।
दूसरे पृष्ठ पर क्योंकि प्रकाश किरण n अपवर्तनांक के माध्यम से वायु में प्रवेश करती है इसलिए अपवर्तन के सूत्र में n के स्थान पर 1n लिखने पर
1/nv−1(v.−t)=1n−1R2 . . . . . . .
पतले लेन्सों के लिए t का मान v. की तुलना में उपेक्षणीय है अतः v की तुलना में t को छोड़ने पर समीकरण (2) का स्वरूप निम्न होगा -
1v−nv.=−(n−1)R2 . . . . . . (3)
समीकरण (1) तथा (3) को जोड़ने पर
1v−1u=(n−1)(1R1−1R2) . . . . (4)
जब वस्तु अनन्त पर स्थित होगी, तो प्रतिबिम्ब लेन्स के द्वितीय फोकस (मुख्य फोकस) पर बनेगा। अर्थात u=∞ , तब v=f जहाँ पर f लेन्स की द्वितीय फोकस दूरी (मुख्य फोकस दूरी) है।
समीकरण (4) में मान रखने पर
1f−1∞=(n−1)(1R1−1R2)
या 1f=(n−1)(1R1−1R2) . . . (5)
इस समीकरण को लेंस मेकर (लेंस निर्माता) सूत्र कहते है।
Topper's Solved these Questions
Similar Questions
एक छोटी दूरबीन के अभिदृश्यक तथा नेत्रिका की फोकस दूरियाँ क्रमशः 192 cm तथा 8cm है। इसकी आवर्धन क्षमता तथा दोनों लैंसों के बीच की दूरी ज्ञात कीजिए।
View Solutionपार्श्विक विस्थापन किसे कहते हैं ? किसी दर्पण की फोकस दूरी तथा वक्रता त्रिज्या में सम्बन्ध स्थापित कीजिए।
अथवा
अवतल दर्पण के लिये किरण चित्र बनाकर सिद्ध कीजिए कि दर्पण की फोकस दूरी उसकी वक्रता त्रिज्या की आधी होती है।
View Solutionउस भौतिक राशि का नाम लिखिए जिसका मात्रक जूल/कूलॉम है। बताइये कि यह राशि सदिश है या अदिश।
View Solutionचिन्ह-परिपाटी | अवतल दर्पण द्वारा प्रतिबिम्ब बनना
View Solutionअवतल दर्पण द्वारा प्रतिबिम्ब बनना
View Solutionसमतल दर्पण | समतल दर्पण द्वारा प्रतिबिम्ब का बनना | गोलीय दर्पण का परिचय
View Solutionदर्पण द्वारा प्रतिबिम्बों का निर्माण || Part -1
View Solutionउत्तल तथा अवतल दर्पण से प्रतिबिम्ब का बनना
View Solutionदर्पण समीकरण पर महत्वपूर्ण प्रश्न |गोलिए दर्पण द्वारा प्रतिबिम्ब निर्माण
View Solutionदर्पण का परिचय |समतल दर्पण के द्वारा प्रतिबिम्ब का बनना
View Solutionअवतल दर्पण के द्वारा विभिन्न स्थितियों पर बिम्ब के लिए प्रतिबिम्ब का निर्माण
View Solutionगोलीय दर्पण के भाग|उत्तल दर्पण तथा अवतल दर्पण द्वारा प्रतिबिम्ब बनने के नियम|OMR|Summary
View Solutionअवतल दर्पण के द्वारा प्रतिबिम्ब बनना|OMR|Summary
View Solutionअवतल दर्पण द्वारा प्रतिबिम्ब बनाना|अवतल दर्पण के उपयोग|उत्तल दर्पण द्वारा प्रतिबिम्ब बनाना|उत्तल दर्पण के उपयोग|OMR|Summary
View Solutionउत्तल लेंस द्वारा प्रतिबिम्ब का बनना|अवतल लेंस द्वारा प्रतिबिम्ब बनने के नियम|OMR|Summary
View Solutionअवतल लेंस द्वारा प्रतिबिम्ब का बनना|अवतल लेंस द्वारा प्रतिबिम्ब का बनना|OMR|Summary
View Solution
